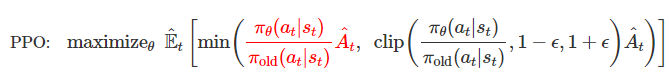PPO(Proximal Policy Optimization)
현재 Policy를 가능한 빠르게 향상시키되, 성능이 발산 해버릴 정도로 너무 Policy가 급격하게 바뀌는 것을 억제
PPO 구조
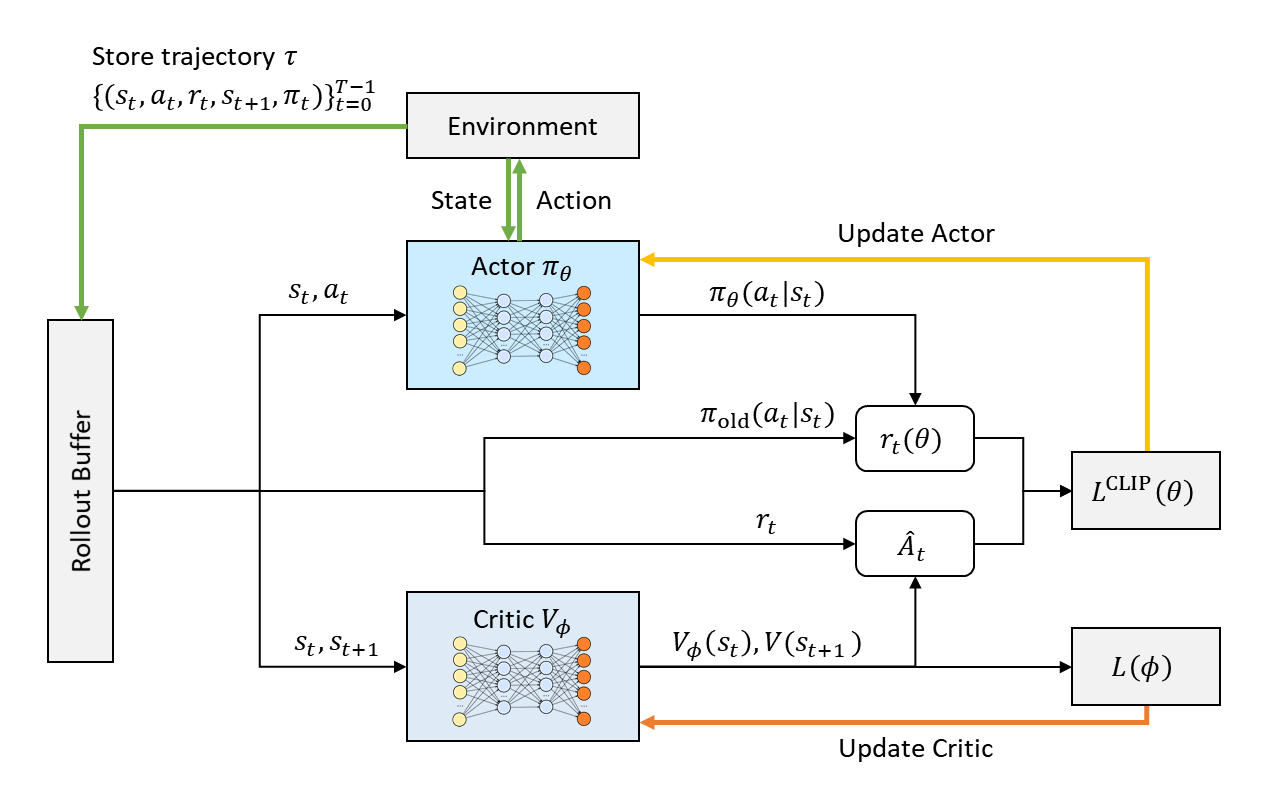
초록선
- 상호작용: 현재 정책을 따르는 Actor (πθ)가 환경과 직접 상호작용하여 경험 데이터를 수집합니다.
- 데이터 생성: 특정 상태(st)에서 행동(at)을 수행하고, 그 결과로 보상(rt)과 다음 상태(st+1)를 관측합니다.
- 데이터 저장: 이 경험의 궤적(trajectory)은 Rollout Buffer라는 임시 저장 공간에 보관됩니다. 저장되는 정보는 다음과 같습니다.
- (상태, 행동, 보상, 다음 상태, 행동 확률)
- (s t,a t,r t,s t+1,πθ(at∣st))
Advantage 계산 (Critic 활용)
- Advantage(A^t)의 정의: 현재 상태(s t)에서 특정 행동(a t)을 하는 것이 평균적으로 얼마나 더 좋은지를 나타내는 지표
- Critic(V ϕ )의 역할: 상태의 가치(Value)를 예측하는 신경망으로, Advantage를 계산하는 데 핵심적인 역할
- Advantage 추정: Critic을 활용한 간단한 Advantage 추정식
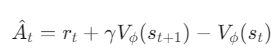
즉, Advantage는 실제 얻은 보상과 예측 가치를 통해 계산된 값(Target)과 현재 상태의 가치 예측치 사이의 차이(TD-Error)를 의미하며, 행동의 좋고 나쁨을 판단하는 기준
Actor (정책) 업데이트 — PPO의 핵심
- Actor는 Advantage(A^ t)를 사용하여 "좋았던 행동"의 확률은 높이고 "나빴던 행동"의 확률은 낮추도록 정책(π θ)을 업데이트합니다.
- 확률 비율(Probability Ratio) 계산
- 업데이트하려는 새 정책(π θ)과 데이터를 수집했던 과거 정책(π old) 사이의 비율을 계산합니다.
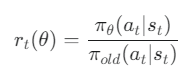
- Clipped Surrogate Objective 함수
- PPO는 정책이 한 번에 너무 크게 변하는 것을 막기 위해 Clipped Surrogate Objective라는 독창적인 목적 함수를 사용합니다.
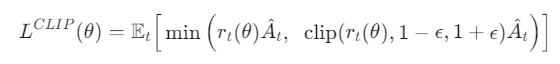
- PPO는 정책이 한 번에 너무 크게 변하는 것을 막기 위해 Clipped Surrogate Objective라는 독창적인 목적 함수를 사용합니다.
Critic (가치 함수) 업데이트
- 손실 함수: 예측한 가치와 실제 보상에 기반한 목표값(Target) 사이의 평균 제곱 오차(Mean Squared Error, MSE)를 최소화하는 방향으로 업데이트합니다.
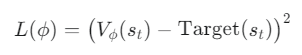
Surrogate Objective (대리 목적 함수)
어떻게 하면 데이터를 재사용해서 효율적으로 학습할 수 있을까?
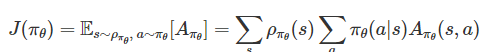
𝜌𝜋𝜃(𝑠): 현재 정책 𝜋𝜃를 따를 때 상태 𝑠를 방문할 확률(상태 방문 빈도)
πθ(a∣s): 상태 S에서 행동 a를 할 확률
Aπθ(s,a): 상태 S에서 행동 a를 했을 때, 평균적인 행동보다 얼마나 좋은지(Advantage)
-> 정책을 따르면 얼마나 좋은 행동을 자주 하는가
- 문제점
- 𝜌𝜋𝜃(𝑠)는 현재 정책에 의존
- 정책이 조금만 업데이트 되어도 상태 방문 빈도가 바뀜
- 따라서 매번 새 데이터를 수집해야만 𝐽(𝜋𝜃)를 계산할 수 있음 → 데이터 비효율적
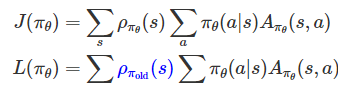
- 핵심 차이:
- 𝜌𝜋𝜃(𝑠)→ 𝜌𝜋𝑜𝑙𝑑(𝑠)로 변경
- 즉, 현재 정책의 상태 방문 분포 대신 이전 정책에서 수집한 분포를 사용
Importance Sampling
- 우리는 과거 정책 𝜋𝑜𝑙𝑑으로 수집한 데이터 (𝑠,𝑎)를 사용해 새로운 정책 𝜋𝜃를 학습하고 싶다.하지만 𝜋𝑜𝑙𝑑 분포로 얻은 데이터와 𝜋𝜃 분포가 다르기 때문에 그대로 사용할 수 없다.
-> 차이를 보정
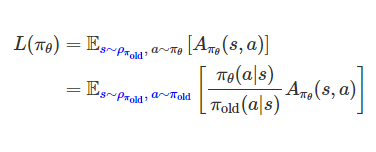
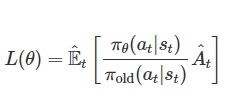
GAE(Generalized Advantage Estimation)
PPO의 Actor는 Advantage 𝐴^𝑡를 보고 학습한다.
- Advantage를 추정하는 기존 두 가지 방법은 극단적:
- Monte Carlo: Low Bias, High Variance → 정확하지만 불안정
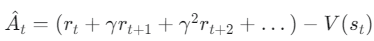
- TD(1-step): High Bias, Low Variance → 안정적이지만 부정확
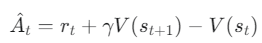
- Monte Carlo: Low Bias, High Variance → 정확하지만 불안정
∴ Advantage를 TD error(δ)의 지수 가중합으로 정의
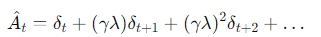
δ t: 현재 시점의 TD error (안정적이지만 근시안적).
δ t+1: 다음 시점의 TD error.
γ: 미래 보상에 대한 할인율(discount factor)로, 원래 강화학습에 있던 개념입니다.
λ: GAE에서 새로 도입된 파라미터로, 미래의 TD error들을 얼마나 신뢰할지를 결정하는 가중치입니다. 이것이 GAE의 핵심입니다.
λ (람다)의 역할
Bias–Variance Trade-off를 조절하는 핵심 파라미터
- λ=0: TD 방식과 동일 → High Bias, Low Variance
- λ=1: Monte Carlo 방식과 동일 → Low Bias, High Variance
- 0<λ<1: 두 방식의 절충점
PPO Argorithm

[루프 개요]
- for iteration = 1.. : 학습 전체 반복
[1) 데이터 수집 & 가공]
- 정책 고정: π_old 로 고정
- 롤아웃: N actors로 T 스텝 실행 → 버퍼에 (st, a_t, r_t, s{t+1}, log π_old(a_t|s_t), V(s_t)) 저장
- GAE로 Advantage 계산
δt = r_t + γV(s{t+1}) − V(st)
Â_t = Σ (γλ)^l δ{t+l}
Return: R_t = Â_t + V(s_t)[2) 학습(최적화)]
- K epochs · 미니배치 M으로 여러 번 재사용
- 확률비율 (Importance Ratio)
rt(θ) = πθ(a_t|s_t) / π_old(a_t|s_t)
- 클리핑 목적함수 (Actor)
L^CLIP(θ) = E_t[min(r_t(θ)Â_t, clip(r_t(θ), 1−ε, 1+ε)Â_t)]
- 가치함수 손실 (Critic)
Lv(ϕ) = E_t[(Vϕ(s_t) − R_t)^2]
- (선택) 엔트로피 보너스: 탐색 강화
최종 손실 = −L^CLIP(θ) + cv L_v(ϕ) − c_e E[H(πθ(·|s))]
- 파라미터 업데이트: θ, ϕ 경사하강
[3) 정책 교체]
- θ_old ← θ 로 갱신하고 다음 iteration 진행
[전체 흐름]
Rollout(π_old 고정) → GAE로 Â_t, R_t 계산 → K epochs·미니배치로 L^CLIP 최대화 & Value MSE 최소화 → θ_old 갱신 → 반복[핵심 포인트]
- Importance Sampling: 과거 데이터로 현재 정책 학습 가능
- Clipping: 과도한 업데이트 억제 (안정성)
- GAE(λ): Bias–Variance 절충으로 견고한 Advantage
- Epoch 재사용: 데이터 효율성 상승
PPO (정책 기반):
'어떻게 행동할지'에 대한 정책(전략) 자체를 직접 학습합니다. 현재 자신의 전략으로만 데이터를 수집하고 학습하는 On-policy 방식을 사용하므로 데이터 효율성은 다소 낮지만, 연속적인 행동 제어 등 복잡한 문제에 강점을 보입니다.
Q-러닝 (가치 기반):
'각 행동이 얼마나 좋은지'에 대한 가치(점수표)를 학습합니다. 과거의 낡은 데이터를 포함해 어떤 정책이 만든 데이터든 학습에 사용할 수 있는 Off-policy 방식을 사용합니다. 이 덕분에 데이터 효율성이 매우 높지만, 주로 단순하고 정해진 행동을 하는 문제에 사용됩니다.
- On-policy (온폴리시): 현재 정책이 생성한 데이터로만 학습하는 방식입니다. (예: PPO)
- Off-policy (오프폴리시): 과거 또는 다른 정책이 생성한 데이터를 포함하여 모든 데이터를 학습에 사용하는 방식입니다. (예: Q-러닝)