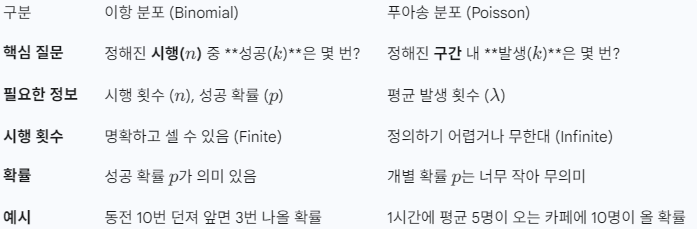
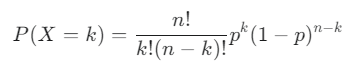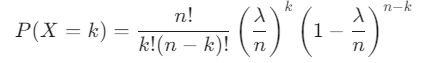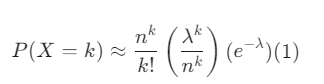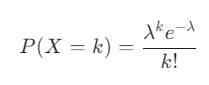이항 분포 (Binomial Distribution)의 기본 개념과 한계
이항 분포는 정해진 횟수(n)의 독립적인 시행에서 성공 확률이 p로 일정한 사건의 성공 횟수(k)를 나타내는 확률 분포입니다.
예를 들어, "사과 10개를 상자에 담을 때, 각 사과가 썩었을 확률이 10%라고 할 때, 썩은 사과가 3개 나올 확률" 같은 문제를 푸는 데 사용됩니다.
- 시행 횟수 (n): 10번 (사과를 담는 행위)
- 성공 확률 (p): 0.1 (사과가 썩었을 확률)
- 성공 횟수 (k): 3번 (썩은 사과가 3개)
이항 분포의 확률 질량 함수(PMF)는 다음과 같습니다.
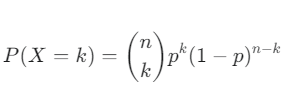
이항 분포의 결정적 한계: 'n'을 알 수 없는 경우
- 1시간 동안 한 웹사이트에 방문하는 사람의 수
- 책 한 페이지에 있는 오타의 개수
- 1년 동안 특정 지역에서 발생하는 교통사고 건수
- 콜센터에 10분 동안 걸려오는 전화의 수
이런 문제들은 이항 분포로 모델링하기 매우 어렵습니다. 왜냐하면 시행 횟수 n을 정의하기가 애매하거나 불가능에 가깝기 때문입니다.
예를 들어, '1시간 동안의 웹사이트 방문자 수' 문제를 생각해 봅시다.
-
시행 횟수 (n)를 무엇으로 잡아야 할까요? 1시간을 1초 단위로 쪼개서 n=3600으로 해야 할까요? 아니면 0.1초 단위로 쪼개서 n=36000으로 해야 할까요? n은 잠재적으로 무한대에 가까워집니다.
-
성공 확률 (p)는 어떻게 될까요? n이 무한대에 가까워진다면, 각 아주 짧은 순간에 방문자가 발생할 확률 p는 0에 극도로 가까워질 것입니다.
이처럼 n은 매우 크고 (n→∞), p는 매우 작은 (p→0) 상황에서 이항 분포는 실용성을 잃게 됩니다. 계산이 불가능할 뿐만 아니라, n과 p를 특정하는 것 자체가 무의미해집니다.
푸아송 분포 (Poisson Distribution)의 등장: 한계의 극복
이러한 이항 분포의 한계를 극복하기 위해 등장한 것이 바로 푸아송 분포입니다. 푸아송 분포는 n과 p를 개별적으로 다루는 대신, 이 둘의 곱인 평균 발생 횟수(λ)라는 새로운 개념을 도입합니다.
λ=n×p
여기서 λ(람다)는 주어진 단위 시간 또는 단위 공간에서 어떤 사건이 평균적으로 발생하는 횟수를 의미합니다.
수학적 유도: 이항 분포에서 푸아송 분포로
푸아송 분포는 사실 이항 분포의 특별한 극한 경우(special limiting case)입니다. 즉, n이 무한대로 가고 p가 0으로 갈 때, 이항 분포는 푸아송 분포에 수렴합니다.
시작점: 이항 분포의 확률 질량 함수
p=λ/n 치환
n이 매우 크고 p가 매우 작으므로, 평균 λ=np는 일정한 값을 유지한다고 가정하고 p=λ/n으로 식을 바꿉니다.
n→∞ 극한 취하기
항들을 조합하여 정리하기