퀵 정렬 quick sort
(1) 사이즈가 n인 하나의 리스트 내의 특정 원소인 피벗(pivot)을 기준으로
(2) 피벗보다 작은 원소들과 큰 원소들을 좌우로 분리하여 두 개의 비균등한 서브리스트를 구성하고
(3) 각 서브리스트를 재귀적은 방식으로 퀵 정렬을 수행하여 정렬한 다음
(4) 두 개의 정렬된 서브리스트를 합하여 전체가 정렬된 리스트가 되게 하는 분할 정복 정렬 알고리즘
- 문제: n개의 정수를 (오름차순으로) 정렬
- 입력: 사이즈가 n인 리스트
- 출력: 오름차순으로 정렬된 n 사이즈 리스트
설계 전략
- 리스트의 사이즈가 1인 경우 해당 리스트는 정렬된 것으로 간주
- 분할: 리스트 내 n개의 원소 정렬 시 피벗을 기준으로 피벗보다 작은 원소들을 피벗의 왼쪽으로 옮기고, 피벗보다 큰 원소들은 모두 피벗의 오른쪽으로 옮겨서 두 개의 서브리스트를 생성. (추가 공간 불필요) 이러한 분할 과정을 partition이라고 함.
- 정복: 각 서브리스트를 재귀적으로 퀵 정렬 ( 두 서브리스트를 각각 정렬하는 것이 부분해)
- 통합: 필요 없음
- 퀵 정렬은 분할 과정이 주요 연산. 통합 불필요. 추가 메모리 불필요.
- 합병 정렬은 합병할 때 계산
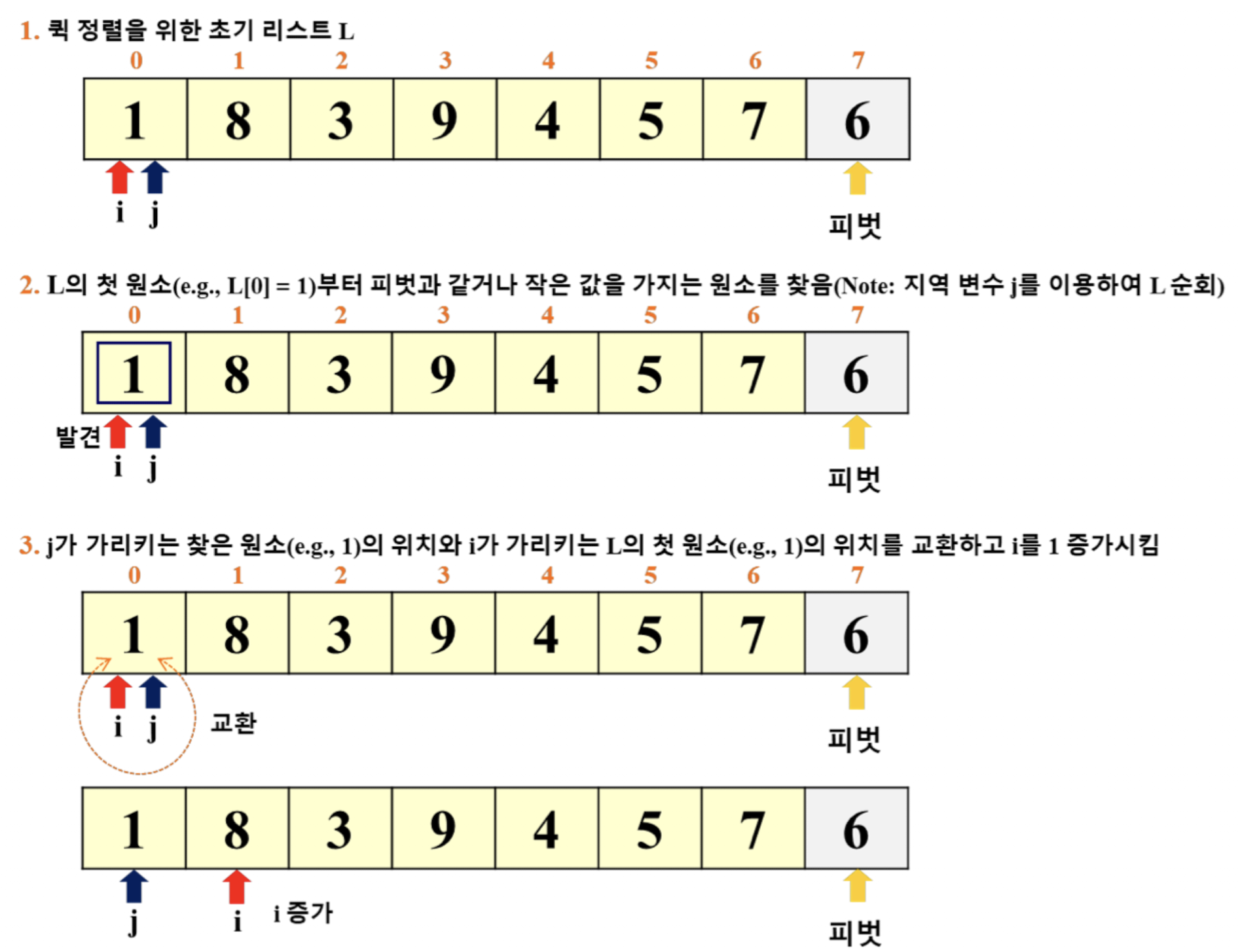
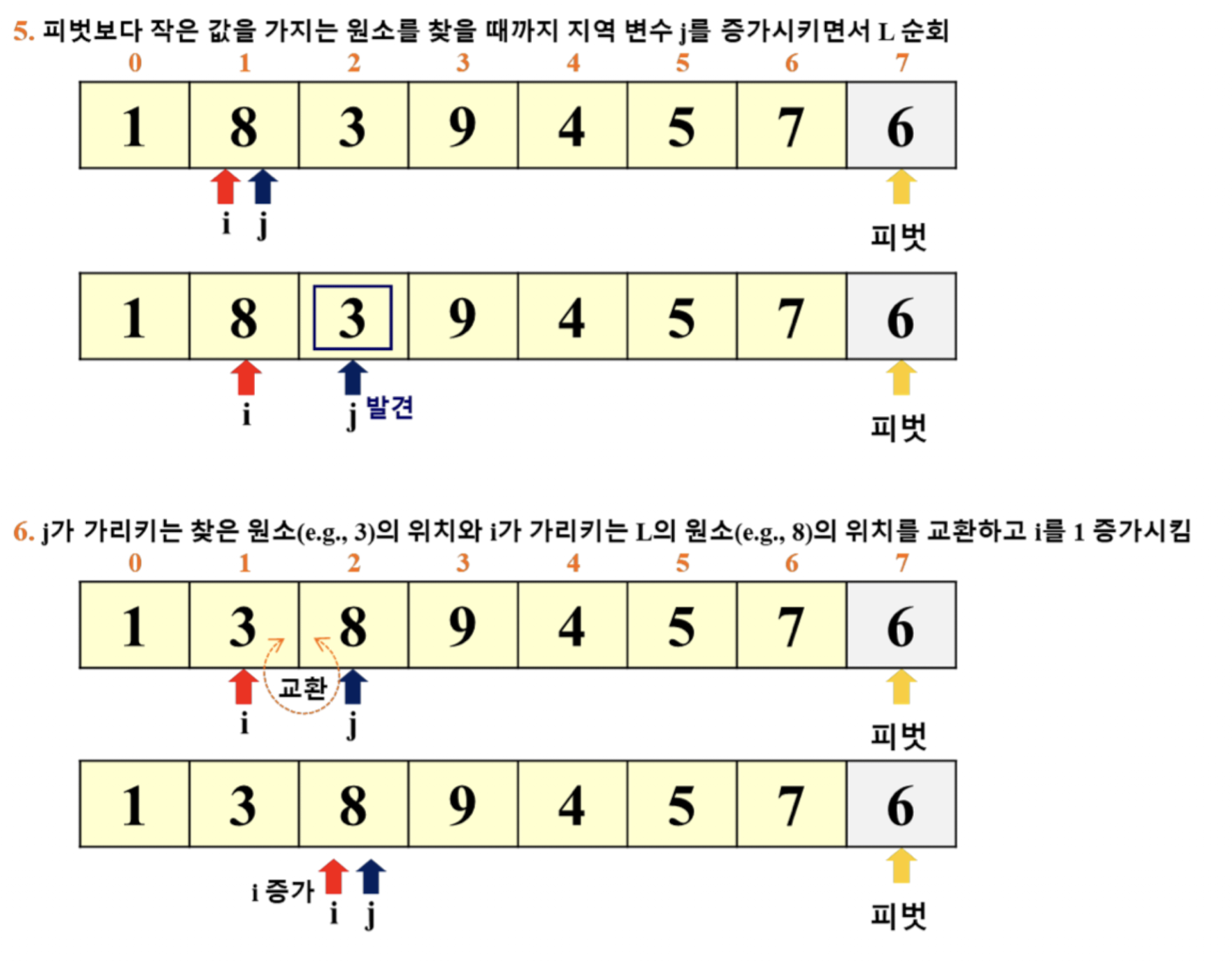
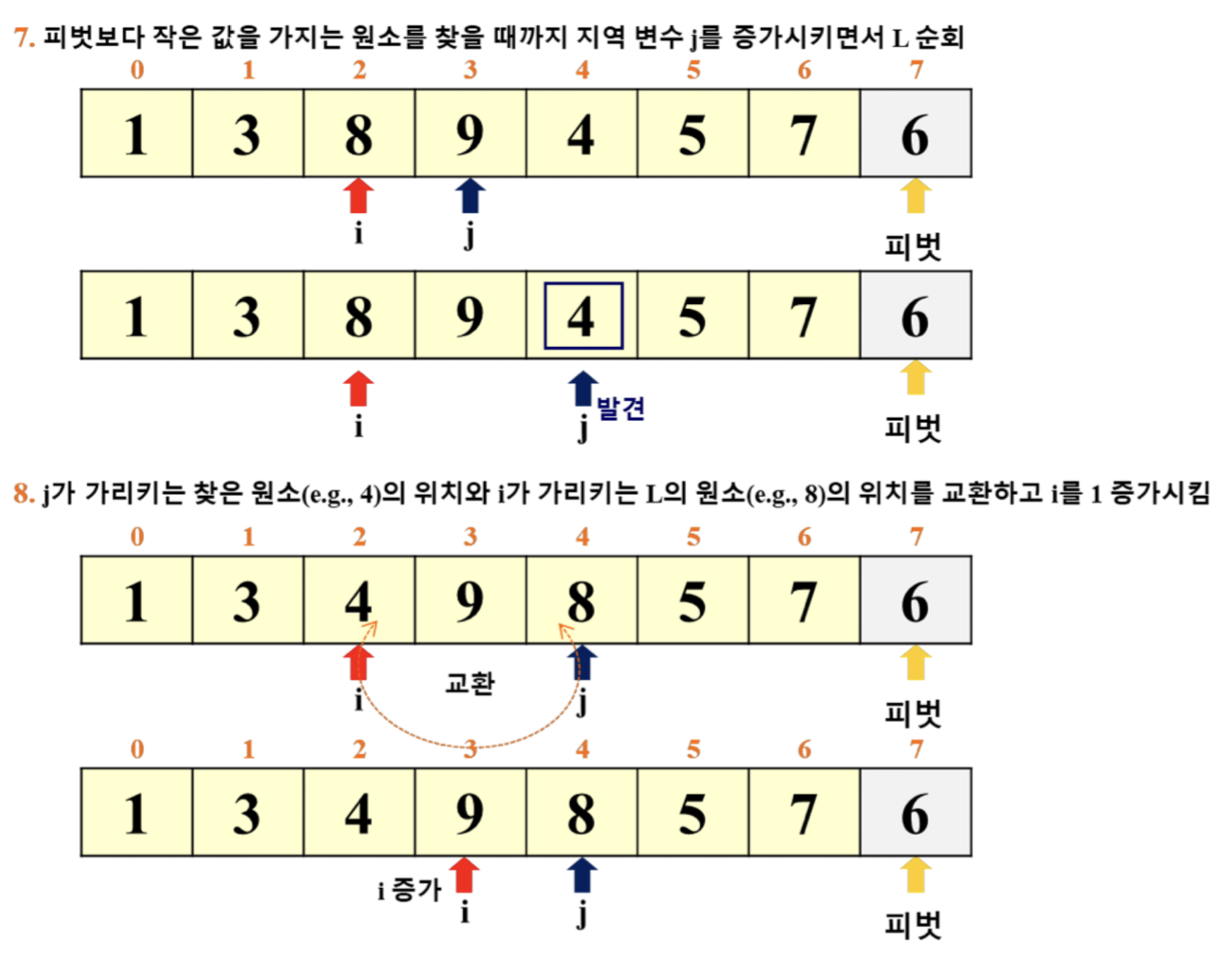
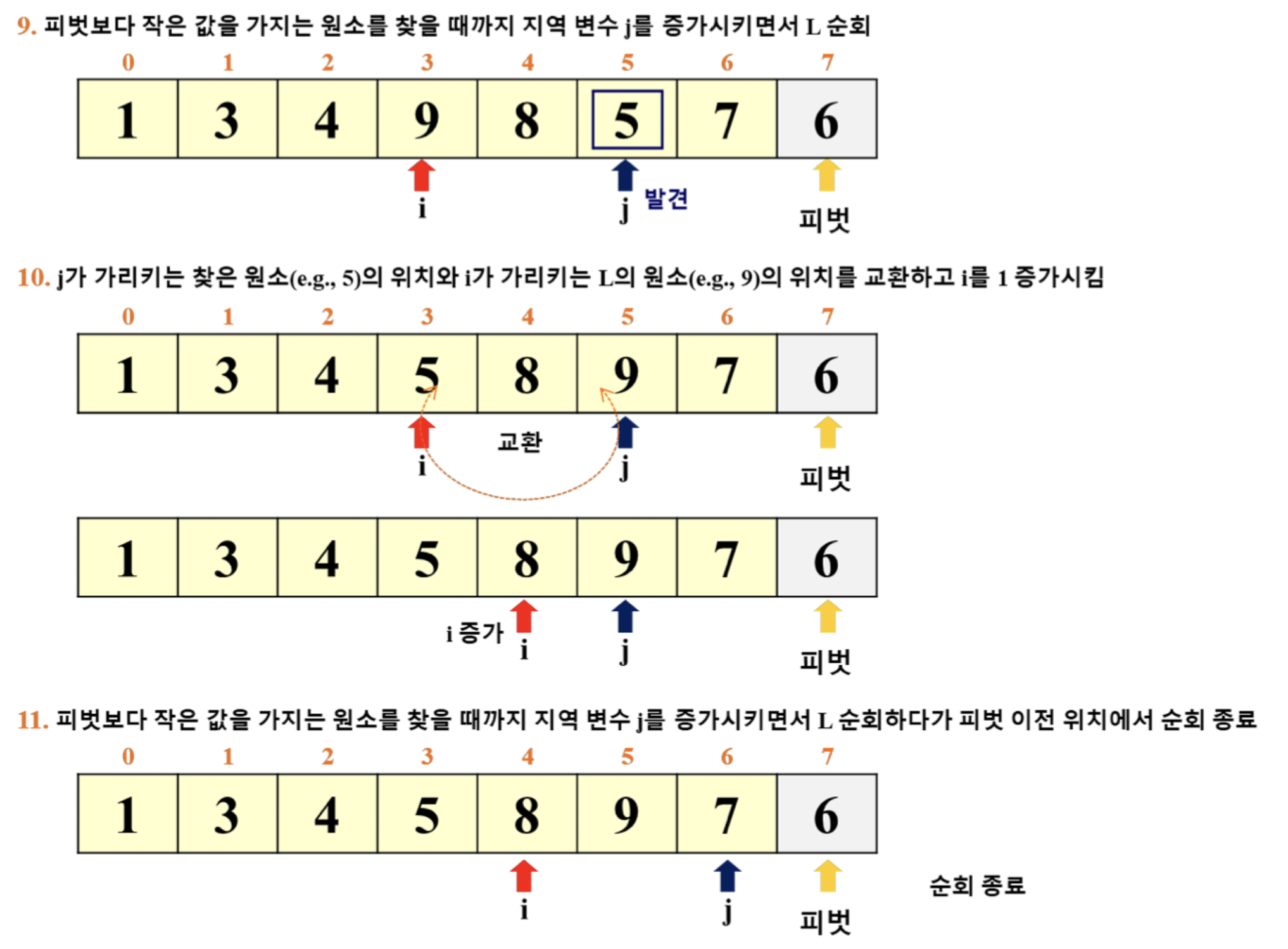
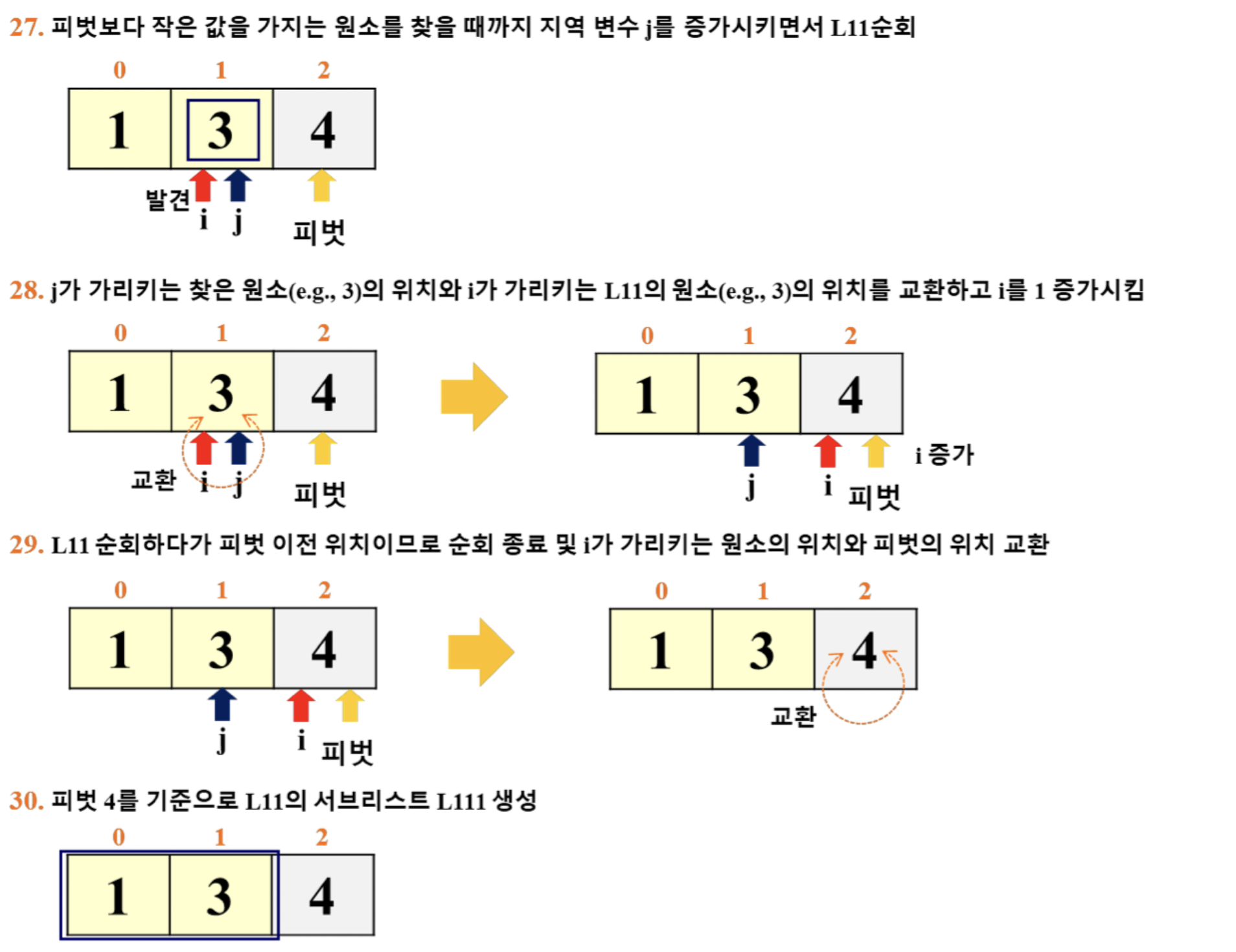
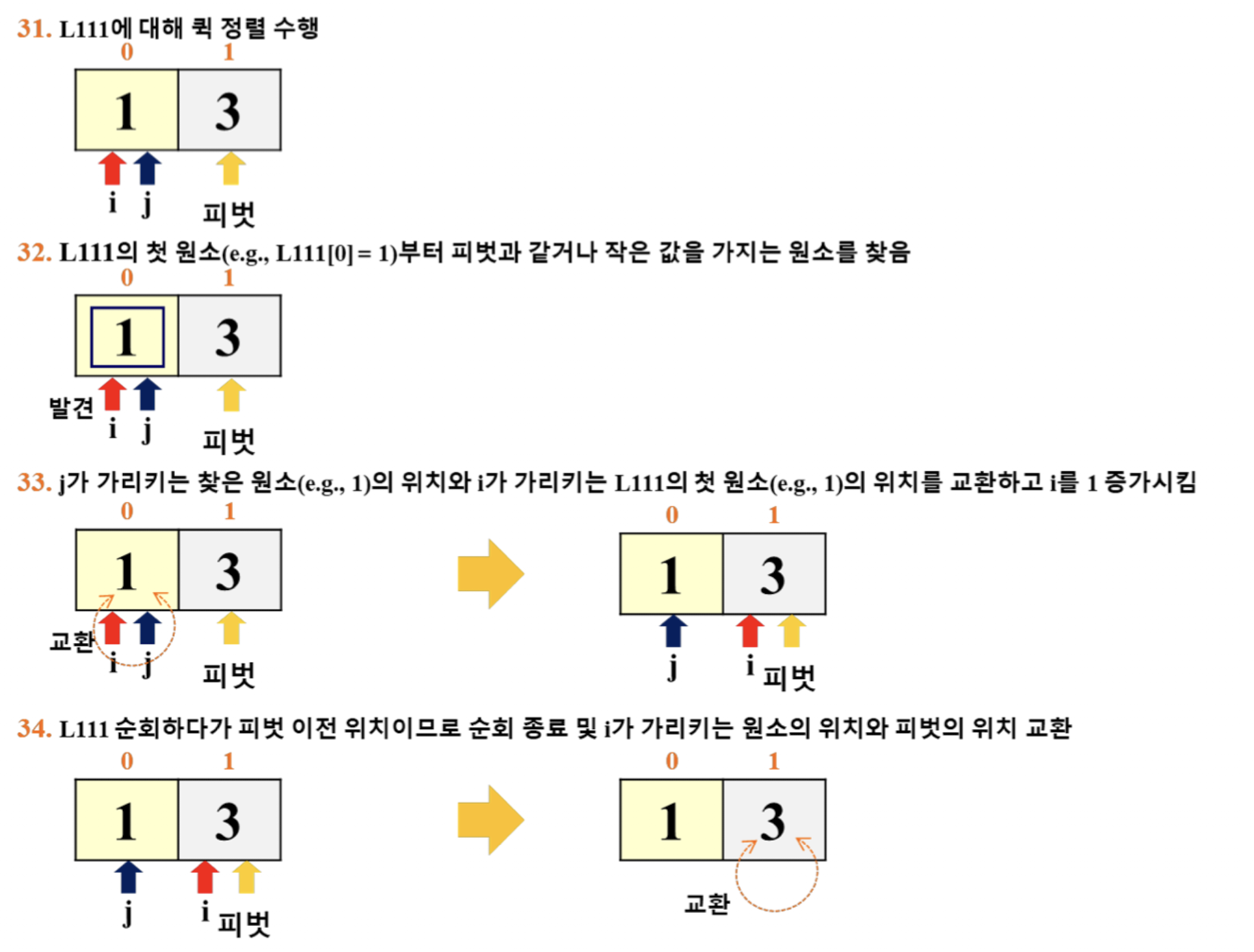
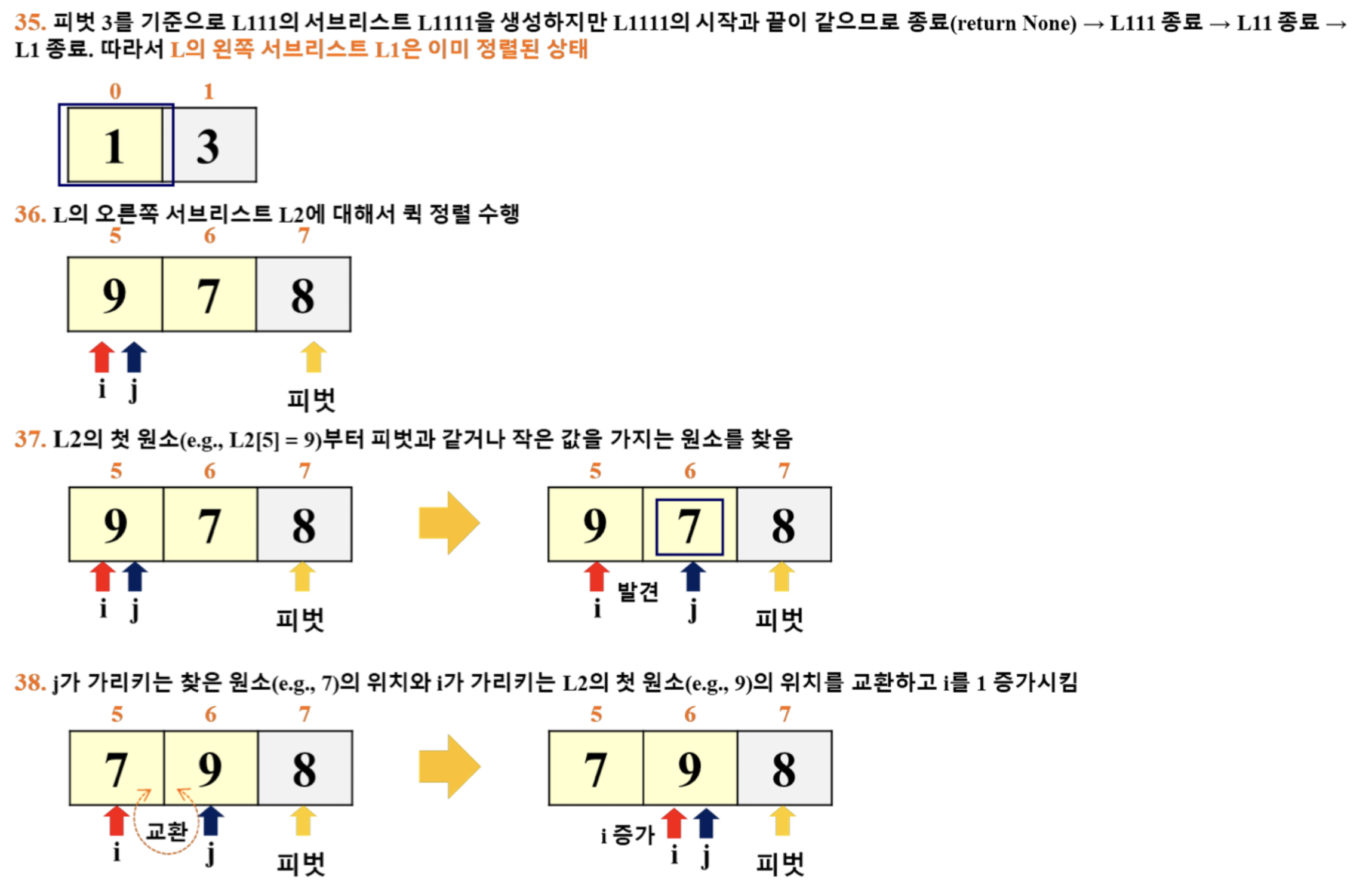
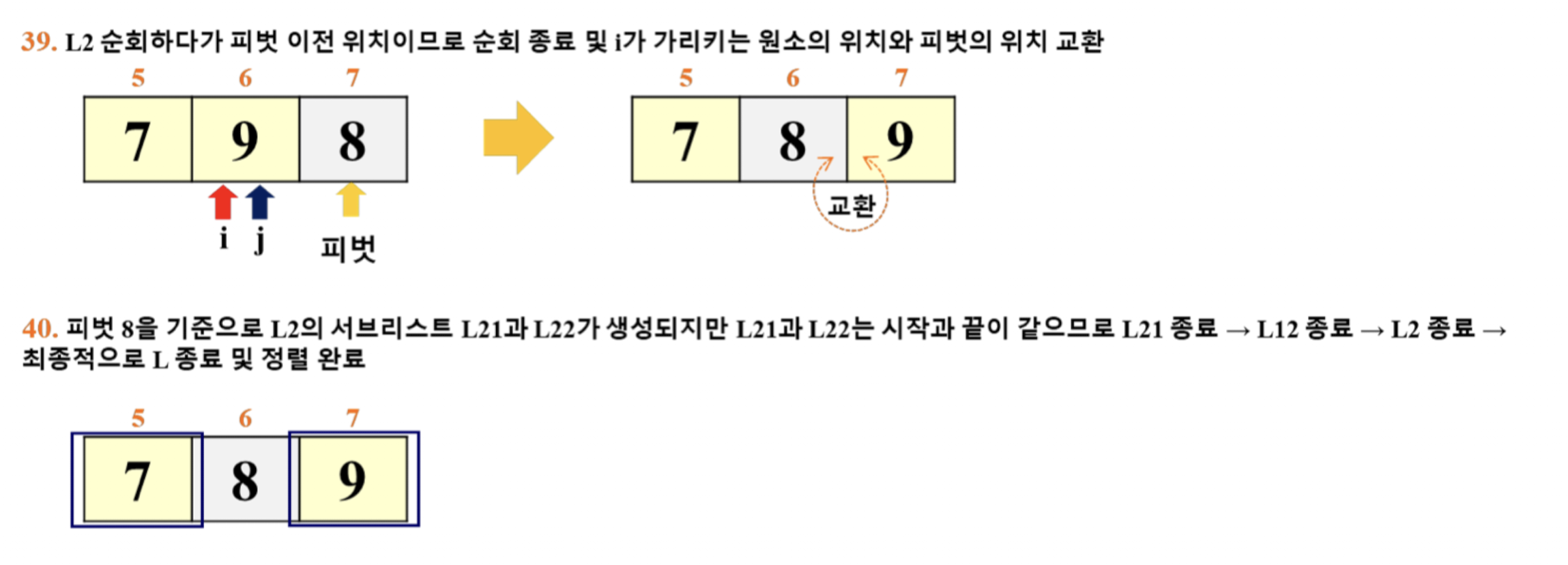
퀵 정렬의 예
- 이 예시에서는 '리스트의 마지막 원소'를 피벗으로 선택
- i: for 루프 탈출 이후의 pivot 위치 파악
- j: for 루프에서 활용 (j += 1)
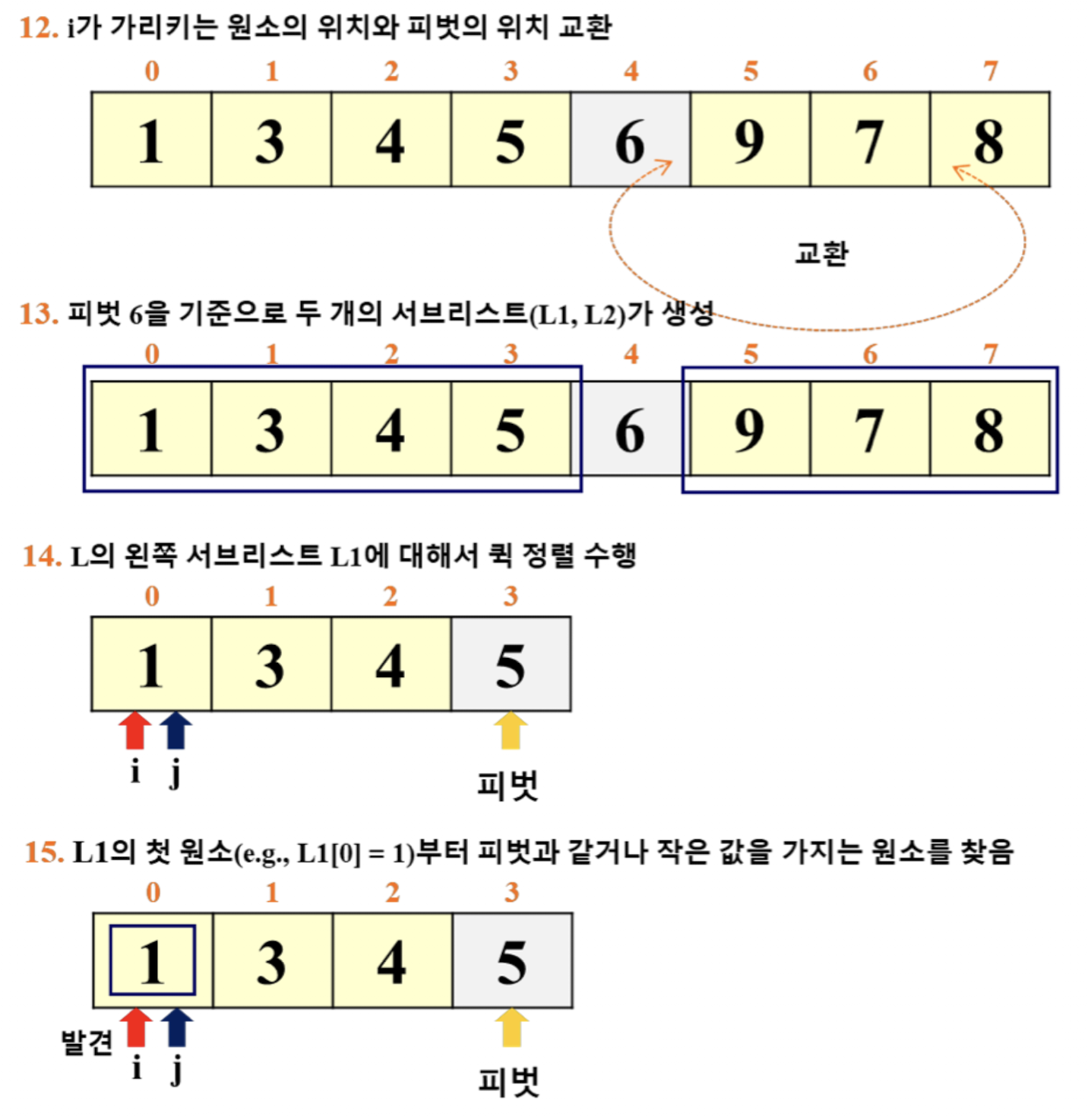
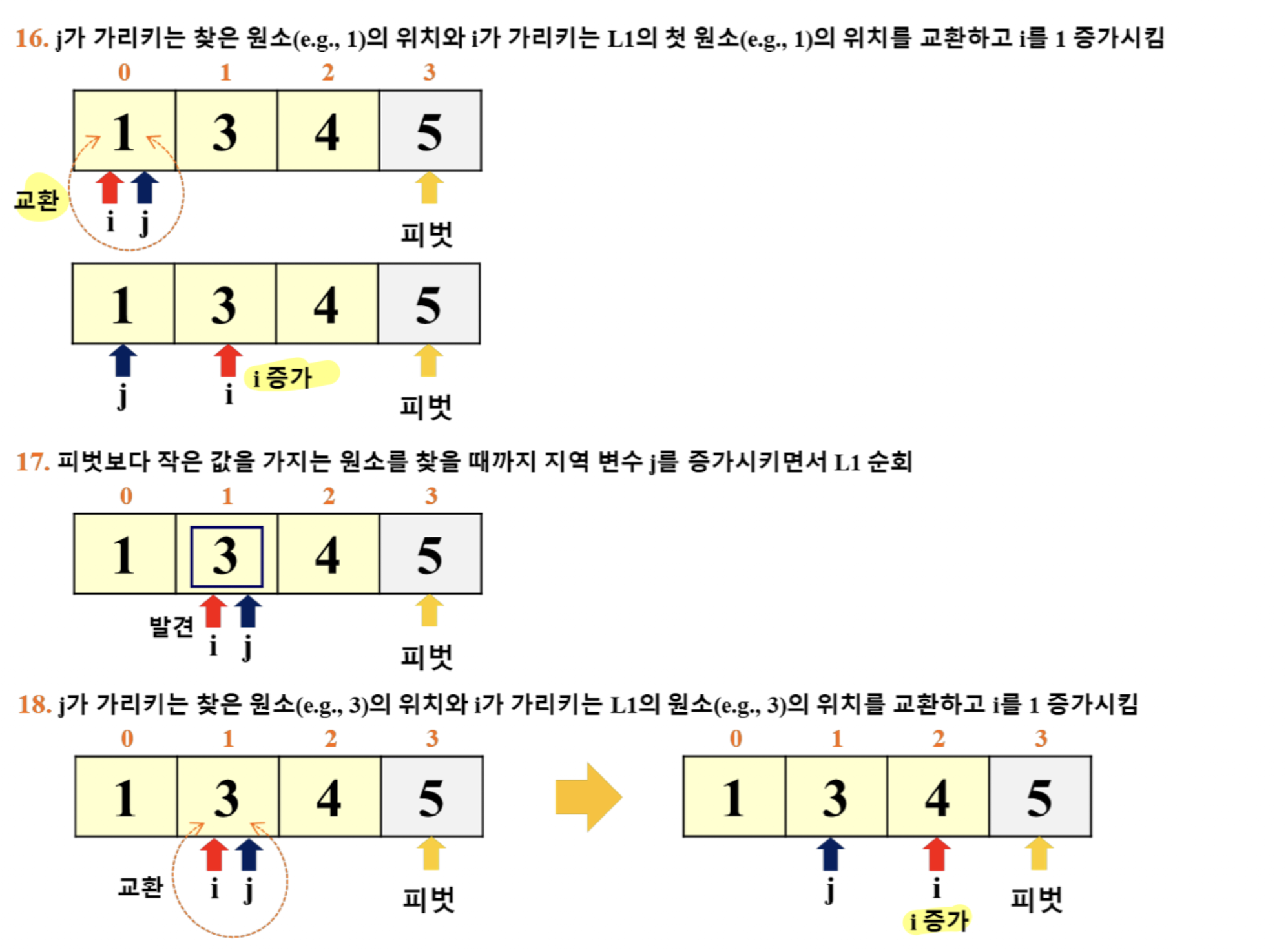
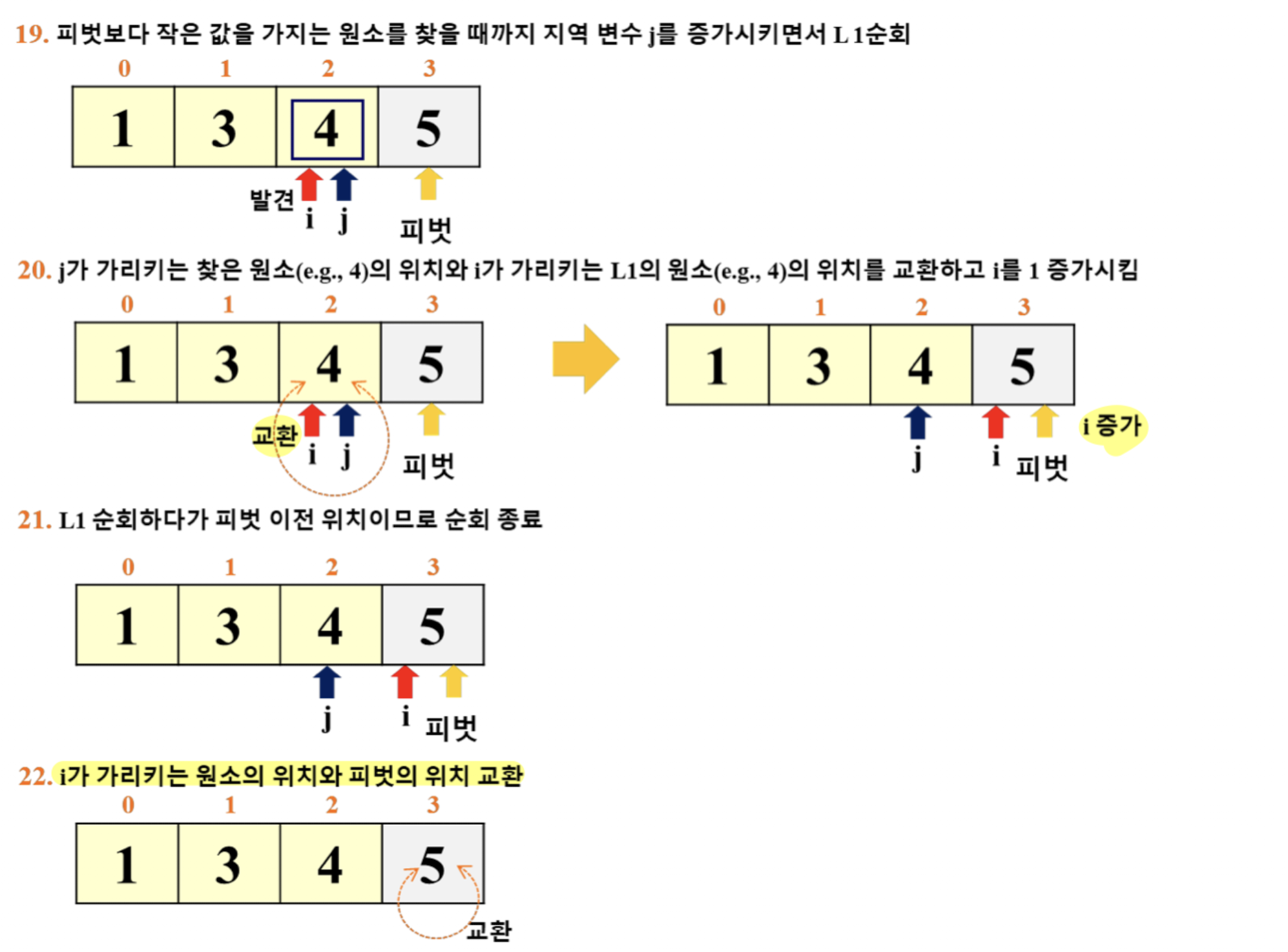
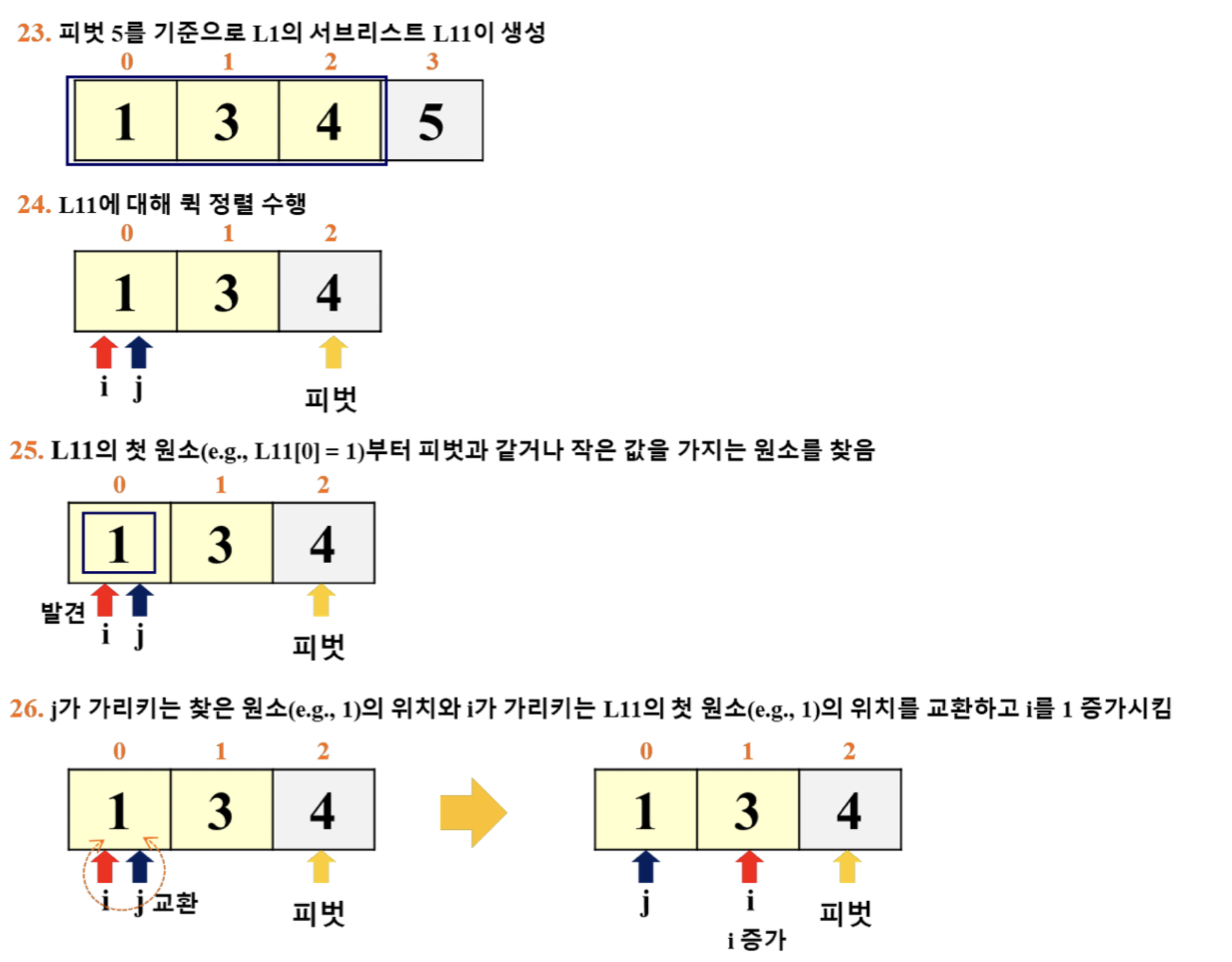
합병 정렬을 위한 함수 partition, qsort 정의
partition 함수
def partition(lst, low, high):
x = lst[high] # 피벗값
i = low # for루프 탈출 후 피벗 위치 기억
for j in range(low, high): # 순회
if lst[j] <= x: # 피벗보다 작은 값 찾으면 swap
lst[i], lst[j] = lst[j], lst[i]
i += 1
lst[i], lst[high] = lst[high], lst[i] # 순회 다 끝나면 i와 pivot 위치 바꿈
return i # pivot 인덱스 반환qsort 함수
def qsort(lst, low, high):
if low < high: ## low == high이면 종료
pi = partition(lst, low, high)
qsort(lst, low, pi-1)
qsort(lst, pi+1, high)실행
lst = [10, 80, 30, 90, 40, 50, 70, 60]
print('정렬 전: \t', end = '')
print(lst)
qsort(lst, 0, len(lst) - 1)
print('정렬 후: \t', end = '')
print(lst)수행시간 분석
- 입력 크기 n = 2^k라고 가정
- 최선의 경우와 평균의 경우: O(n logn)
- 최선의 경우 합병 정렬과 마찬가지로 k만큼 분할하며, 각 분할마다 약 n번의 원소를 비교
- 평균의 경우: 피벗의 인덱스가 리스트 전체게 걸쳐서 균등하게 임의로 결정된다는 가정 하에 O(nlogn)
- 최악의 경우: O(n^2)
- 입력이 이미 정렬되어 있거나 역순으로 정렬되어 있다면 n번 분할하여 각 단계마다 n-1, n-2, ..., 1번의 원소를 비교하므로 n(n-1)/2
특징
- 평균 시간복잡도가 O(nlogn)인 다른 정렬 알고리즘들보다 빠름 (상수적으로)
- 합병 정렬과 다르게 정렬 시 추가 메모리 공간이 필요하지 않음
합병 정렬과의 차이점
- 합병 정렬은 아무 연산 없이 균등한 두 부분으로 분할하는 반면, 퀵 정렬은 분할할 때부터 기준 원소(피벗)를 중심으로 이보다 작은 것은 왼편, 큰 것은 오른편에 위치시킴.
- 즉, 정복(정렬) 과정이 분할 과정과 함께 진행
- 각 부분 정렬이 끝난 후, 합병 정렬은 통합 과정이라는 후처리 작업이 필요하나, 퀵 정렬은 불필요.
