합병 정렬 merge sort
(1) 사이즈가 n인 하나의 리스트를 두 개의 균등한 크기의 서브리스트로 분할하고
(2) 각 서브리스트를 재귀적인 방식으로 합병 정렬을 수행하여 정렬한 다음
(3) 두 개의 정렬된 서브리스트를 합하여 전체가 정렬된 리스트가 되게 하는 분할 정복 알고리즘
- 문제: n개의 정수를 (오름차순으로) 정렬
- 입력: 사이즈가 n인 리스트 L
- 출력: 오름차순으로 정렬된 n 사이즈 리스트
설계 전략
- 리스트의 사이즈가 1인 경우, 해당 리스트는 정렬된 것으로 간주
- 분할: 리스트 L내 n개의 원소 정렬 시 low, mid, high를 찾은 후 (low: 가장 왼쪽 인덱스, mid: 중간 인덱스, high: 가장 오른쪽 인덱스), 두 서브리스트 L[low, mid]와 L[mid+1, high]로 분할 (두 서브리스트가 부분 문제)
- 정복: 각 서브리스트를 재귀적 합병 정렬을 이용하여 정렬 (두 서브리스트를 각각 정렬하는 것이 부분해)
- 통합: 두 서브리스트를 다시 하나의 정렬된 리스트로 합병 (두 개의 부분 해들을 통합)
- 리스트 내 n개의 원소 정렬 시 low, mid, high를 찾은 후, 두 서브리스트 L[low, mid]와 L[mid+1, high]로 분할
- 모든 서브리스트가 1이 될 때까지 재귀적으로 분할
- 분할 과정이 끝나면, n개의 원소를 포함하는 하나의 리스트 (정렬된 L)가 생성될 때까지 각각의 서브리스트를 정렬하면서 결합
- 합병 정렬은 분할 과정보다 통합 과정이 주요 연산
합병 정렬의 예

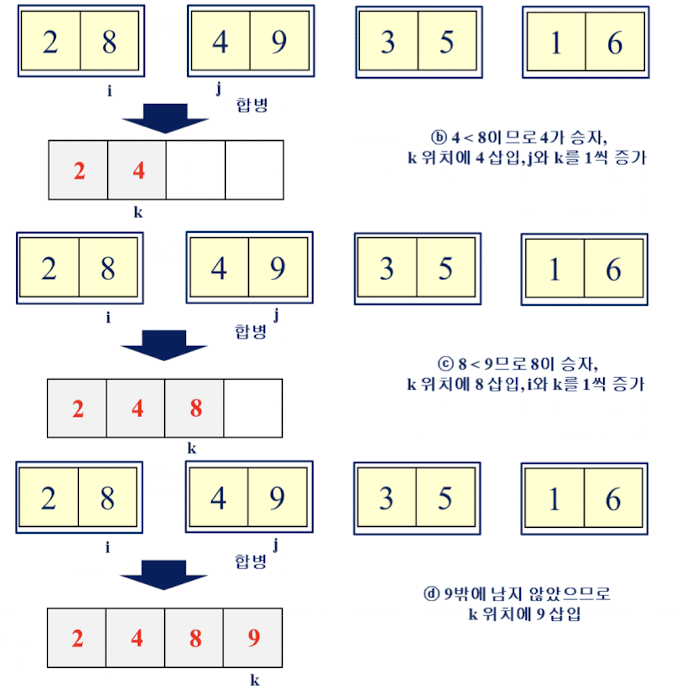
오른쪽도 같은 방법으로 합병 진행
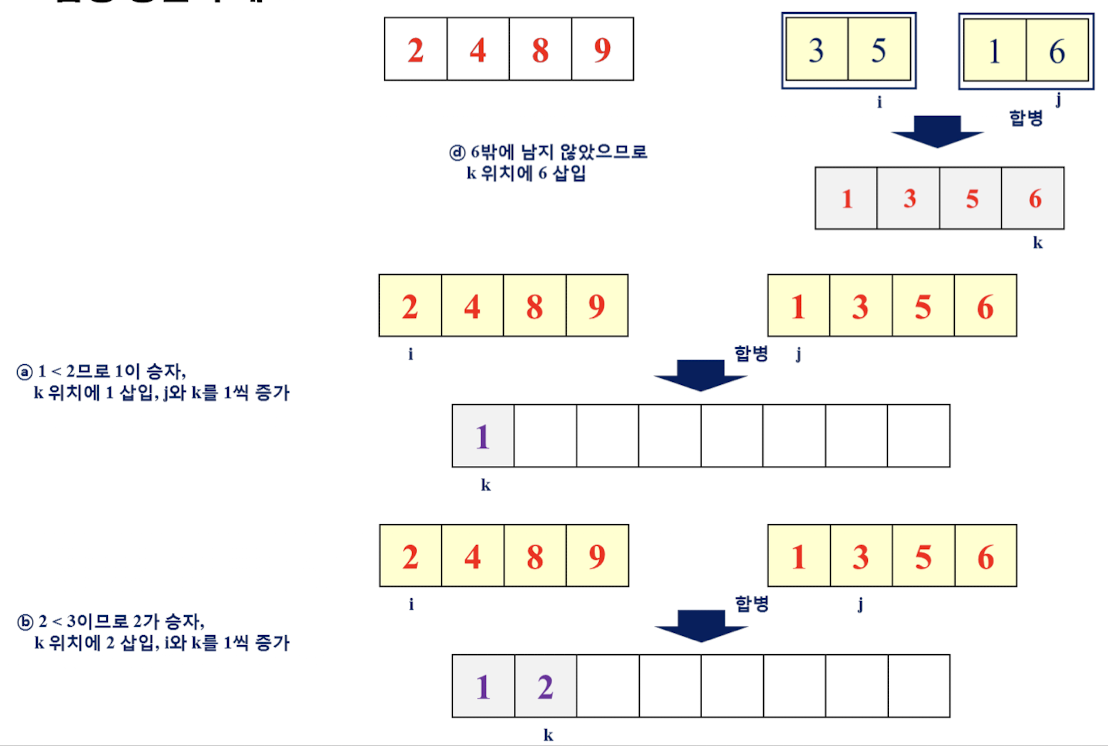
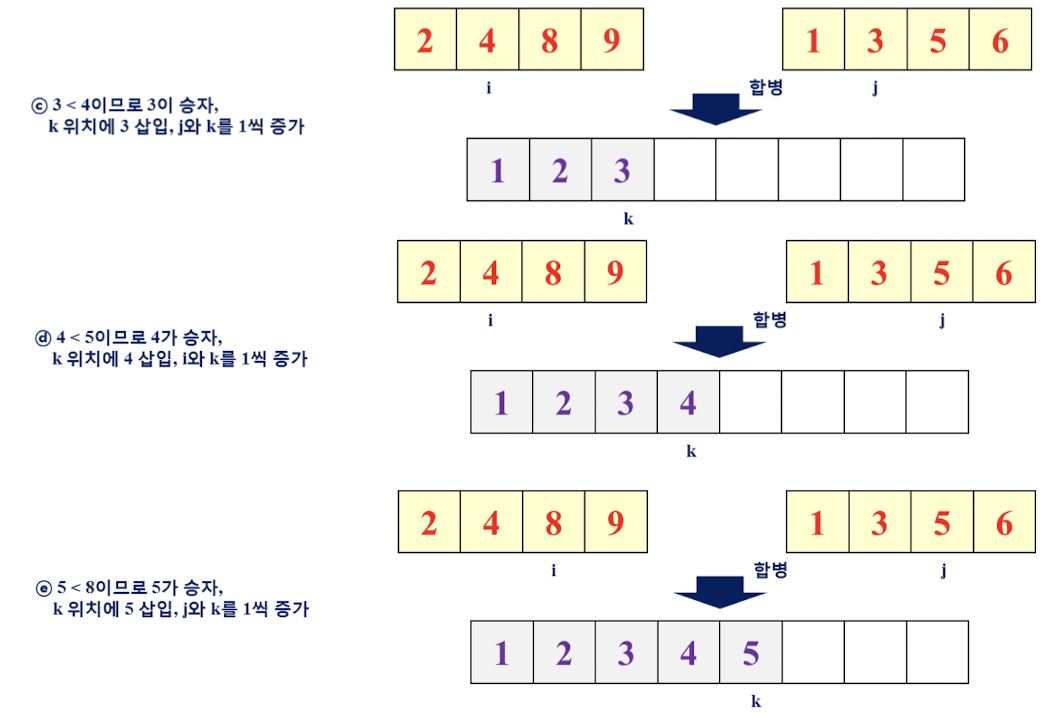
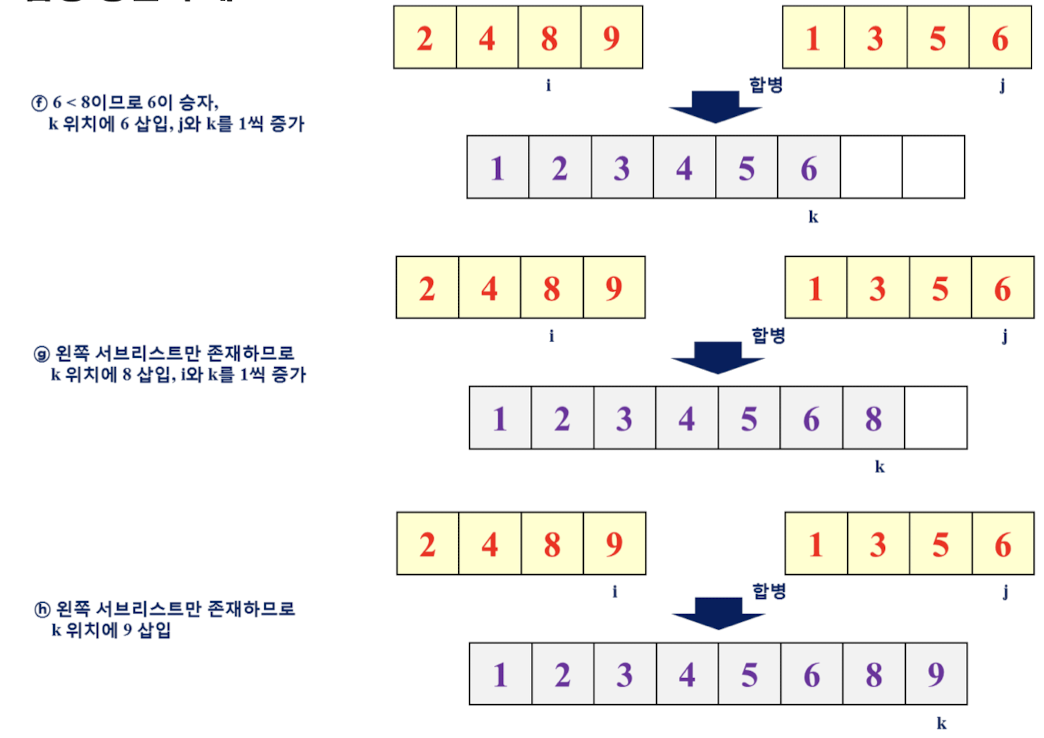
합병 정렬을 위한 함수 merge, merge_sort 정의
merge 함수
def merge(lst, temp, low, mid, high):
i = low # i: 왼쪽 트리
j = mid + 1 # j: 오른쪽 트리
for k in range(low, high + 1): # 순회 루프
if i > mid: # i 끝남. 즉, 왼쪽 트리 순회 종료, 오른쪽 트리만 남음.
temp[k] = lst[j]
j += 1
elif j > high: # j 끝남. 즉, 오른쪽 트리 순회 종료, 왼쪽 트리만 남음.
temp[k] = lst[i]
i += 1
elif lst[j] < lst[i]:
temp[k] = lst[j]
j += 1
else:
temp[k] = temp[i]
i += 1
for k in range(low, high+1):
lst[k] = temp[k] # temp에 있는 정렬된 값들을 lst에 넣어주기merge_sort 함수
def merge_sort(lst, temp, low, high):
if high <= low: # 크기가 1인 리스트
return None
mid = low + (high - low) // 2
merge_sort(lst, temp, low, mid) # 왼쪽 트리
merge_sort(lst, temp, mid + 1, high) # 오른쪽 트리
merge(lst, temp, low, mid, high) # 합치기실행
lst = [54, 88, 77, 26, 93, 17, 49, 10, 17, 77, 11, 31, 22, 44, 17, 20]
temp = [None] * len(lst)
print('정렬 전: \t', end = '')
print(lst)
merge_sort(lst, temp, 0, len(lst) - 1)
print('정렬 후: \t', end = '')
print(lst)결과:
정렬 전: [54, 88, 77, 26, 93, 17, 49, 10, 17, 77, 11, 31, 22, 44, 17, 20]
정렬 후: [10, 11, 17, 17, 17, 20, 22, 26, 31, 44, 49, 54, 77, 77, 88, 93]수행 시간 분석
- 리스트 사이즈(입력 사이즈) n = 2^k라고 가정
- 합병 정렬의 분할은 각 분할 단계마다 리스트의 중간 인덱스 계산과 2번의 재귀 호출이므로 상수 시간 c가 소요되며, lg n 단계가 존재하므로 c log n
- 단위 연산은 통합(합병)에서의 비교 연산 (혹은 복사 연산)으로 각 통합 단계마다 (n-1)번 비교하며 (또는 n번 복사하며), lg n 단계가 존재하므로 시간복잡도는 O(n log n)
특징
- 입력에 민감하지 않음: 어떤 입력에 대해서도 항상 O(n log n) 수행 시간 소요
- 정렬 시 추가 메모리 공간이 필요함 (입력 크기만큼의 공간)
