문제 1. 변동계수 구하기

회사 주식에 투자하고자 합니다. 하지만 보수적인 나는 변동성이 크지 않은 회사를 골라 안정적인 투자를 희망합니다. 이를 위해 2가지 회사로 좁혔고 A,B회사의 6일간 주가 데이터를 수집하였습니다. Numpy 혹은 Pandas를 이용하여 회사의 변동계수를 구해봅시다.

• cv_a_np : a 회사의 변동계수
• cv_b_np : b 회사의 변동계수

풀이

• 변동계수 = 표준편차 / 평균
• 표본 표준편차는 자유도를 설정해야 함.

import numpy as np
com_a = [76300, 77400, 77900, 77200, 76900, 78800]
com_b = [6400, 7000, 7400, 6900, 7300, 7600]

# 평균 구하기
a_mean = np.mean(com_a)
b_mean = np.mean(com_b)

# 표본표준편차 구하기
a_std = np.std(com_a, ddof = 1)
b_std = np.std(com_b, ddof = 1)

cv_a_np = a_std / a_mean
cv_b_np = b_std / b_mean

# 결과 출력
print(f'A회사의 변동계수 {cv_a_np:.3f}')
print(f'B회사의 변동계수 {cv_b_np:.3f}')

결과:

A회사의 변동계수 0.011
B회사의 변동계수 0.060

+) Numpy.std() vs Pandas.std()

• 자유도의 디폴트 값이 다르다.

  • np.std(ddof = 0)
  • pd.Series.std(ddof = 1)

문제 2. 신뢰구간 구하기

평균이 $\mu$ 이고 표준편차가 $\sigma = 8$ 인 정규분포를 따르는 모집단에서 크기가 25인 표본을 추출하여 평균을 계산하였더니 $\bar{x}$가 42.7 이다. 이때 $\mu$에 대한 95% 신뢰 구간을 구하라.

풀이

• 표본의 수가 30보다 작더라도 모표준편차를 알고 있다면 t검정이 아닌 Z검정
• scipy에는 z검정으로 신뢰구간을 구하는 모듈이 없기 때문에 직접 계산해야 함

$S$는 모집단의 표준편차, $n$은 표본의 개수, $\mu$는 우리가 추정하고자 하는 모집단의 평균

import scipy.stats as stats
import numpy as np

# 주어진 값들
sigma = 8  # 모집단의 표준편차
n = 25  # 표본 크기
x_bar = 42.7  # 표본 평균
confidence_level = 0.95  # 신뢰 수준

se = sigma / np.sqrt(n)
lower_bound = x_bar - 1.96 * se
upper_bound = x_bar + 1.96 * se

print(f"95% 신뢰 구간: ({lower_bound:.2f}, {upper_bound:.2f})")

결과:

95% 신뢰 구간: (39.56, 45.84)

문제 3. 이표본 t 검정

• 목초에 따른 우유의 생산량을 알아보기위하여 25마리 젖소를 대상으로 3주동안 임의로 추출된 12마리 젖소에게 건조시킨 목초를 주고 13마리 젖소에게는 들판에서 말린 목초를 주었다.
• 두 종류의 모 표준편차는 같다고 가정하고 또한 우유생산량의 자료는 정규분포를 따른다고 가정한다.
• 자연적으로 말린 목초의 사육하는 젖소의 우유생산량이 인공적으로 말린 목초로 사용하는 젖소보다 많다고 할 수 있는지 유의수준 0.05 에서 검정하세요. (단측 검정)

풀이

• 이분산 t 검정
• 등분산과 정규분포 가정은 생략 가능 (조건에 주어졌으므로)
• scipy.stats.ttest_ind(data1, data2, equal_var = True, alternative = 'greater')로 단측 검정

import numpy as np
from scipy import stats

nature = [44, 44, 56, 46, 47, 38, 58, 53, 49, 35, 46, 30, 31]  # 자연적으로 말린 목초
artificial = [35, 47, 55, 29, 40, 39, 32, 41, 42, 57, 51, 39]  # 인공적으로 말린 목초

t_stats, p_value = stats.ttest_ind(nature, artificial, equal_var=True, alternative='greater')

print('H0: 귀무가설은 "자연적으로 말린 목초로 사육한 젖소의 우유 생산량과 인공적으로 말린 목초로 사육한 젖소의 우유 생산량에는 차이가 없다." 이다.')
print('H1: 대립가설은 "자연적으로 말린 목초로 사육한 젖소의 우유 생산량이 인공적으로 말린 목초로 사육한 젖소의 우유 생산량보다 많다." 이다.')
print(f't-통계량: {t_stats}')
print(f'p-값: {p_value}')
if p_value < 0.05:
    print('귀무가설을 기각합니다.')
else:
    print('귀무가설을 기각하지 않습니다.')

결과:

H0: 귀무가설은 "자연적으로 말린 목초로 사육한 젖소의 우유 생산량과 인공적으로 말린 목초로 사육한 젖소의 우유 생산량에는 차이가 없다." 이다.
H1: 대립가설은 "자연적으로 말린 목초로 사육한 젖소의 우유 생산량이 인공적으로 말린 목초로 사육한 젖소의 우유 생산량보다 많다." 이다.
t-통계량: 0.605564440457578
p-값: 0.2753667443616386
귀무가설을 기각하지 않습니다.

문제 4. 카이제곱 검정

• 다음 click_rate 데이터는 헤드라인별 클릭과 클릭하지 않은 수 에 대한 데이터입니다.
• 귀무가설과 대립가설을 설정하세요.
• 카이제곱 검정 수행하여 실제로 클릭률에 대한 차이가 있는지 유의수준 0.05 에서 검정해보세요.

풀이

카이제곱 분포로 독립성 검정

import pandas as pd
from scipy import stats
# URL 로 데이터 가져오기
url = "https://raw.githubusercontent.com/gedeck/practical-statistics-for-data-scientists/master/data/click_rates.csv"
click_rate  = pd.read_csv(url)
clicks = click_rate.pivot(index='Click', columns='Headline', values='Rate')
display(clicks)

chi2_stat, pvalue, dof, expected = stats.chi2_contingency(clicks, correction=True)

print('H0: 귀무가설은 "헤드라인과 페이지 클릭율에는 관련이 없다." 이다.')
print('H1: 대립가설은 "헤드라인과 페이지 클릭율에는 관련이 있다." 이다.')
print(f'chisq: {chi2_stat}')
print(f'pvalue: {pvalue}')

# 결론
alpha = 0.05  # 유의수준
if pvalue < alpha:
    print("귀무가설 기각: 헤드라인과 페이지 클릭율에는 관련이 있다.")
else:
    print("귀무가설 채택: 헤드라인과 페이지 클릭율에는 관련이 없다.")

결과:

H0: 귀무가설은 "헤드라인과 페이지 클릭율에는 관련이 없다." 이다.
H1: 대립가설은 "헤드라인과 페이지 클릭율에는 관련이 있다." 이다.
chisq: 1.6659394708658917
pvalue: 0.4347562562343731
귀무가설 채택: 헤드라인과 페이지 클릭율에는 관련이 없다.

+) correction = True 는 무엇인가

Yate's correction

• 자유도가 낮은 경우 검증이 잘 작동하지 않는다.
• 자유도가 1인 경우 (데이터가 2*2인 경우) Yate's correction을 이용하여 조금 더 엄격하게 검증.
• 위 case는 2 * 3 경우라서 자유도가 2이기 때문에 교정 사례에 해당 안 됨.

문제 5. 중심극한정리(CLT) 데이터셋 생성

• scipy.stats 모듈에서 다음 분포를 생성하고 히스토그램으로 표현하기(subplots권장)
• 변수
  • 이항 분포 샘플 변수명 binomial_data: 확률 0.5의 시행을 10번 시행했을때 성공할 갯수의 1000개의 표본 생성
    • ex) 동전 10번 던졌을때 앞면이 나올 수 있는 수는 0부터 10개
  • 균등 분포 샘플 변수명 uniform_data : 시작 0, 끝 10의 표본 1000개 생성
  • 표준 정규 분포 샘플 변수명 normal_data : 표본 1000개 생성
• 위 분포 3개를 히스토그램으로 표현하되 plt.subplots(1,3)을 이용하여 동시에 표현하고, bins 는 20개로 설정

풀이

• numpy를 이용한 풀이

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)

# scipy를 통한 샘플 생성
# binomial
binomial_data = np.random.binomial(n=10, p=0.5, size=1000)

# uniform
uniform_data = np.random.uniform(0, 10, 1000)

# normal
normal_data = np.random.normal(0, 1, 1000)

# 시각화
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5))

ax1.hist(binomial_data, bins = 20, color = 'blue')
ax1.set_title('Binomial Distribution')

ax2.hist(uniform_data, bins = 20, color = 'green')
ax2.set_title('Uniform Distribution')

ax3.hist(normal_data, bins = 20, color = 'red')
ax3.set_title('Normal Distribution')

for a in [ax1, ax2, ax3]:
    a.set_xlabel('Value')
    a.set_ylabel('Frequency')
    
plt.show()

결과:

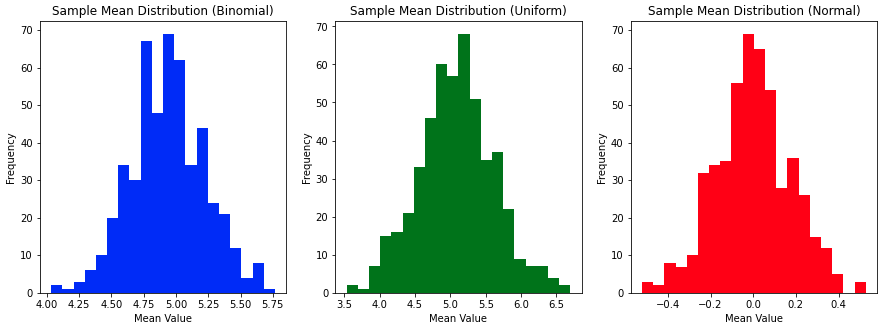
문제 6. 중심극한정리(CLT) 표본의 평균 시각화

• numpy.choice 함수를 이용하여 각 분포 평균을 내고 이를 500번 반복하여 표본 평균을 생성해 봅시다. (ex bionmial_data 에서 30개씩 뽑아 500번 반복)
• 표본의 평균들을 히스토그램으로 시각화여 정규분포를 따르는지 확인해봅시다.
• 변수
  • num_samples : 표본추출할 횟수
  • sample_means: 딕셔너리 자료형으로 Binomal, Uniform, Normal 의 Key값을 가지며 해당하는 values들은 각 30개씩 복원추출하여 뽑은 샘플의 평균 값을 저장. 이를 총 500번 진행

풀이

import numpy as np
import matplotlib.pyplot as plt

num_samples = 500
sample_means = {
    "Binomial": [],
    "Uniform": [],
    "Normal": []
}

for i in range(500):
    sample_means['Binomial'].append(np.random.choice(binomial_data, 30, replace = True).mean())
    sample_means['Uniform'].append(np.random.choice(uniform_data, 30, replace = True).mean())
    sample_means['Normal'].append(np.random.choice(normal_data, 30, replace = True).mean())


# 시각화
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5))

ax1.hist(sample_means['Binomial'], bins = 20, color = 'blue')
ax1.set_title('Sample Mean Distribution (Binomial)')

ax2.hist(sample_means['Uniform'], bins = 20, color = 'green')
ax2.set_title('Sample Mean Distribution (Uniform)')

ax3.hist(sample_means['Normal'], bins = 20, color = 'red')
ax3.set_title('Sample Mean Distribution (Normal)')

for a in [ax1, ax2, ax3]:
    a.set_xlabel('Mean Value')
    a.set_ylabel('Frequency')
    
plt.show()

결과: