4. 알고리즘

Elenaljh·2023년 6월 20일

CS50

목록 보기

6/14

4. 알고리즘

1. 검색 알고리즘

1. 선형 검색 (Linear search)

(배열이 정리되어 있지 않은 경우) 배열의 인덱스를 처음부터 끝까지 하나씩 증가시키면서 방문해 그 값이 속하는지 검사
<의사코드>

For i from 0 to n-1
	If i'th element is 50
		Return true
Return false

2. 이진 검색 (Binary search)

(배열이 정리된 경우) 중간 인덱스부터 검색 시작
1. 찾는 값 < 찾은 값: 작은(왼쪽) 인덱스 검색
2. 찾는 값 > 찾은 값: 큰 (오른쪽) 인덱스 검색
수업 첫 시간에 예시로 들었던 전화번호부에서 Mike Smith찾기와 비슷함
<의사코드>

If no items
	Return false
If middle item is 50
	Return true
Else if 50 < middle item
	Search left half
Else if 50 > middle item
	Search right half

2. 알고리즘 표기법

1. Big-O

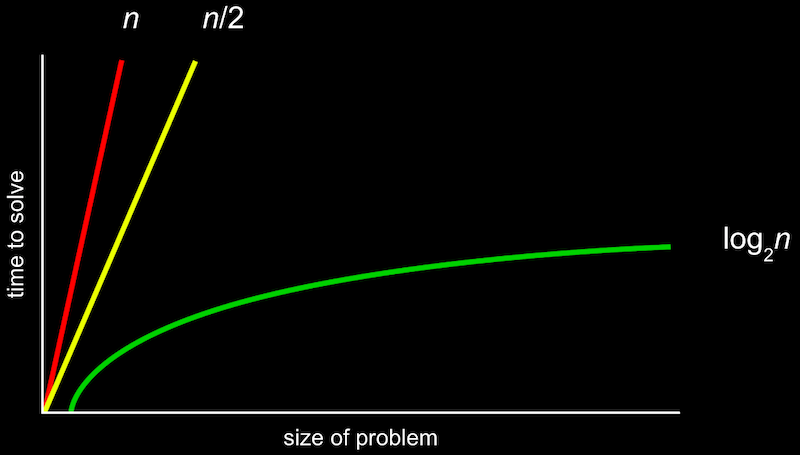
Big-O: On the order of 의 약자 ("~만큼의 정도로 커지는"이라고 이해할 수 있음)
알고리즘 실행 시간의 상한을 나타냄. 즉, 알고리즘이 가장 느릴 때 얼마나 걸리는지 나타냄
n이 매우 커질 경우 O(n) == O(2/n)이므로 빨간색과 노란색 그래프는 같게 취급함.
대표적인 실행시간(Running time)은 다음과 같다.
- O(n^2)
- O(n log n)
- O(n) : 선형검색
- O(log n) : 이진검색
- O(1)

2. Big Ω

Big Ω: 알고리즘 실행 시간의 하한을 나타냄. 즉, 알고리즘이 가장 빠를 때 얼마나 걸리는지 나타냄.
대표적인 Big Ω 표기
- Ω(n^2)
- Ω(n log n)
- Ω(n) : 배열 안에 존재하는 값의 개수 세기
- Ω(log n)
- Ω(1) : 선형검색, 이진검색

3. 생각해보기

:bulb: 실행시간의 상한이 낮은 알고리즘과 하한이 낮은 알고리즘 중 뭐가 더 좋을까?
상한이 낮은 알고리즘이 좋다. 최악의 경우를 가정했을 때 가장 빠르게 실행되는 알고리즘을 써야 더 안정적이기 때문이다.

3. 선형 검색 (Linear Search)

:pushpin: 키워드: 선형검색, 구조체
1. 선형검색
원하는 원소가 발견될 때까지 처음부터 마지막 자료까지 차례대로 검색한다.
2. 효율성, 비효율성
- 선형검색 알고리즘은 정확하지만 매우 비효율적이다.
- 그러나 자료가 정렬되어있지 않거나 그 어떤 정보도 없어 하나씩 찾아야 하는 경우에 유용하다.
3. 검색 이전에 정렬해야 하는 이유
- 정렬은 시간이 오래 걸리고 공간을 더 차지한다.
- 그러나 추가적으로 정렬을 하면 여러 번 리스트를 검색해야 하거나 매우 큰 리스트를 검색해야 할 경우 시간을 단축할 수 있다.
4. 한 번에 3장의 전화번호부를 살펴본다면 탐색시간은 n/3이 될 것인데, 이런 것도 선형탐색으로 간주한다.

1. 정수형 자료에서 선형검색하기

#include  <cs50.h>
#include  <stdio.h>

int  main(void)
{
	int  numbers[6] = {4, 8, 5, 16, 23, 42};
	int  s;
	for (int  i = 0; i < 6; i++) //50찾기(선형탐색)
	{
		if (numbers[i] == 50)
		{
			printf("Found\n");
			return 0;  //return 0(성공)을 쓰면 성공시 함수가 여기에서 멈춘다.
		}
	}
	printf("Not found");
	return 1;  //실패인 경우 관습적으로 1을 반환한다.
}

2. 문자열 자료에서 선형검색하기

C에서는 names[i] == "EMMA"와 같이 관계연산자 ==은 문자열(string)에 사용할 수 없다. EMMA는 여러 문자(char)의 배열이기 때문에 각 문자열이 같은지 알고싶으면 문자열 속의 문자를 하나씩 비교해야 한다. (JAVA나 Python에서는 가능하지만 C는 로우레벨 언어이기 때문에 안됨)
C에서 문자열을 비교하려면 string.h의 strcmp(string1, string2) 를 사용하면 된다.(두 문자열이 같을 때 0 반환)

#include  <cs50.h>
#include  <stdio.h>
#include  <string.h>

int  main(void)
{
	string  names[4] = {"EMMA", "RODRIGO", "BRIAN", "DAVID"};
	string  numbers[4] = {"010-5555-0100", "010-5555-0101", "010-5555-0102", "010-5555-1012"};  // 주석 1, 2 참고
	for (int  i = 0; i < 4; i++)
	{
		if (strcmp(names[i], "EMMA") == 0)
		{
			printf("%s\n", numbers[i]);
			return  0;
		}
	}
	printf("Not found\n");
	return  1;
}

주석
1. 전화번호를 string처리 하는 이유: 전화번호 안에는 -나 +처럼 숫자가 아닌 것들도 들어감. 그리고 정수형 자료는 0으로 시작되는 숫자에서 앞의 0은 없애버리는데 전화번호에서 앞의 0이 빠지면 곤란해짐
2. 이 경우에는 names 배열과 numbers 배열이 서로 같은 인덱스를 가져야 한다는 한계가 있다. 만약 이 상태에서 names의 배열을 알파벳 순서로 정렬해버린다면 이름과 잘못된 번호가 연결된다.

3. 새로운 자료형으로 구조체 (structure) 정의하기

#include  <cs50.h>
#include  <stdio.h>
#include  <string.h>

//구조체 정의하기  
typedef  struct 		//주석 1 참고 
{
string  name;
string  number; 		//주석 2 참고
}
person; 				//주석 3,4 참고

int  main(void) 
{
	person  people[4]; 			//자료형이 person인 배열 people이 정의됨

	people[0].name = "EMMA";	//주석 5 참고
	people[0].number = "010-5555-0100";

	people[1].name = "RODRIGO";
	people[1].number = "010-5555-0101";

	people[2].name = "BRIAN";
	people[2].number = "010-5555-0102";

	people[3].name = "DAVID";
	people[3].number = "010-5555-0103"; // 중괄호를 사용해서 입력할 수 있지만 그럼 코드가 더 더러워진다고 함

	for (int  i = 0; i < 4; i++)
	{
		if (strcmp(people[i].name, "EMMA") == 0)
		{
			printf("%s\n", people[i].number);
			return  0;
		}
	}
	printf("Not found\n");
	return  1;
}

주석
1. struct:구조체 -C에 미리 정의된 키워드로 여러가지 자료형을 담을 수 있다. struct is a container for multiple data types.
2. struct에 name, number(두 가지 string)을 담을것임
3. person이라는 자료형이 정의됨. 이제 clang은 int, string, char, person, float등의 자료형이 있다고 인식함.
4. 이런걸 보고 캡슐화하여 관련 자료를 관리한다고 한다. (특히 데이터베이스 다룰 때) - "capsulate related information"
5. person이라는 이름의 구조체를 자료형으로 정의하고 person 자료형의 배열을 선언하면 그 안에 포함된 속성값은 '.'으로 연결해서 접근할 수 있다.

4. 생각해보기

:bulb: 전화번호부와 같이 구조체를 정의하여 관리 및 검색을 하면 편리한 예는 또 무엇이 있을까요?
주민등록번호, 학번, 학점 등 두 가지 이상의 정보를 묶어서 관리해야하는 정보.

4. 버블 정렬 (Bubble Sort)

1. 정의

정렬되지 않은 숫자를 정렬하는 방법은 어떤 것이 있을까?
버블 정렬 은 두 개의 인접한 자료 값을 비교하면서 위치를 교환하는 방식으로 정렬하는 방법이다. 간단하지만 단 하나의 요소를 정렬하기 위해 너무 많이 교환하는 낭비가 발생한다.

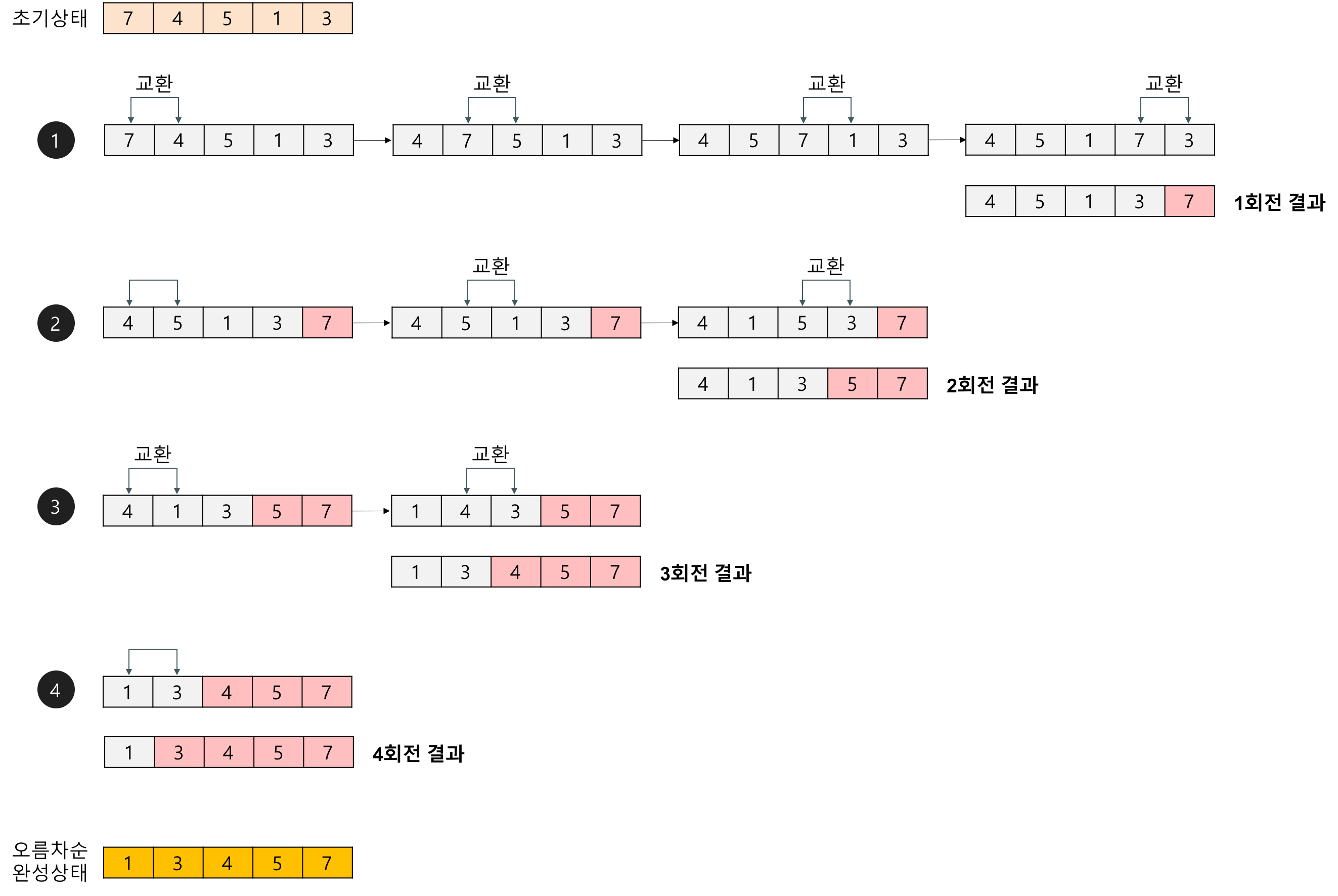
2. 의사 코드

For i from 0 to n-2 
	For j from 0 to n-2-i
		If j'th and j+1th elements out of order
			Swap them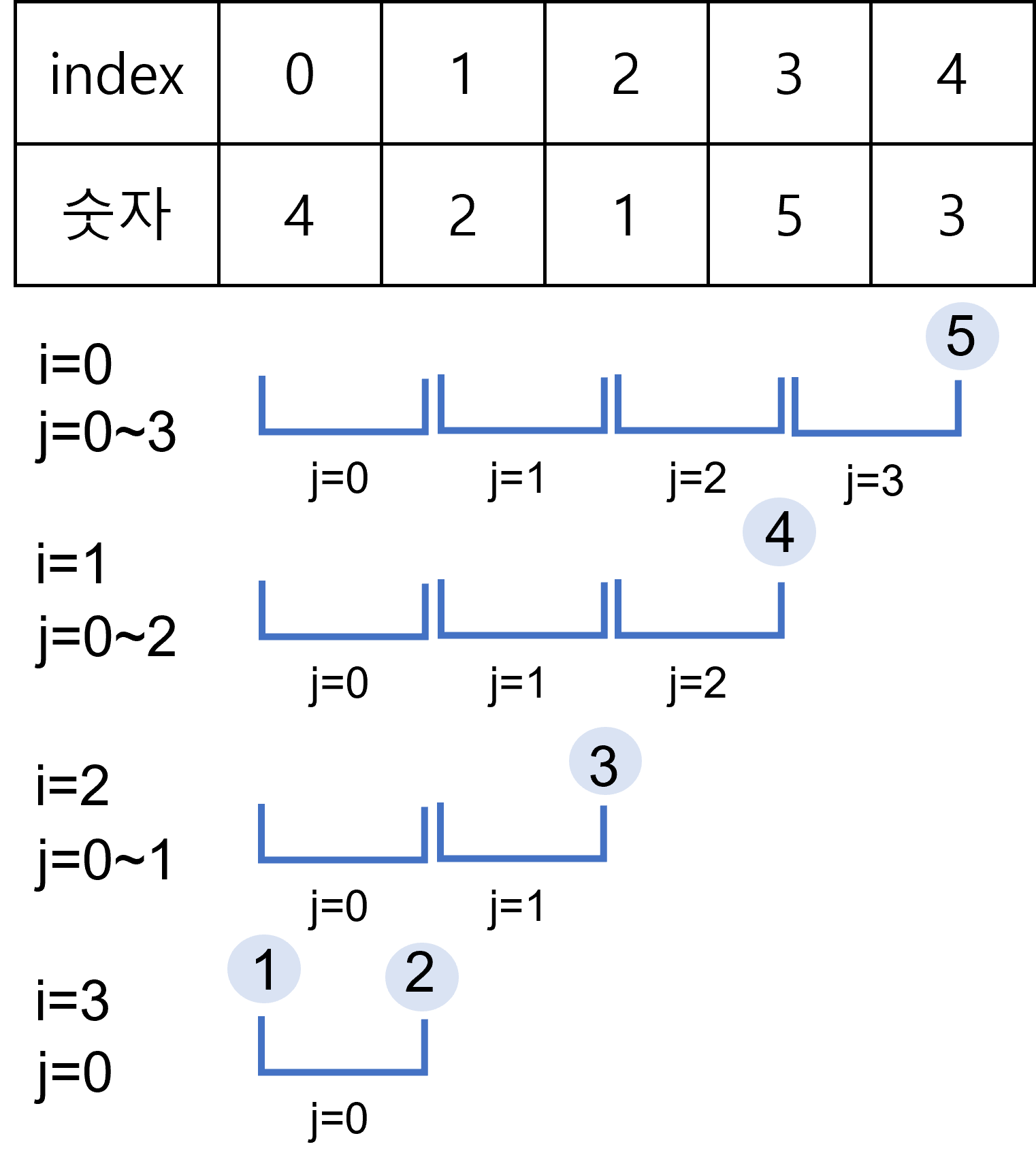

3. O(n^2)

1. 버블정렬 작업 수

버블 정렬을 할 때 필요한 작업의 수는
(n-1) + (n-2) + (n+3) + ... + 2 + 1 = {1+ (n-1)}(n-1) / 2
= n(n-1)/2
= n^2 - n/2
= O(n^2)

2. 빅오 정리

O(n^2) : bubble sort
O(n log n)
O(n) : linear search
O(log n) : binary search
O(1)

O(log n) < O(n) < O(n^2)이므로 이진탐색이 가장 효율적인 것으로 보일 수 있다.
그러나 이진탐색을 하기 위해서는 그 전에 자료가 정렬되어야 한다. 즉, O(n^2)의 작업 수가 추가적으로 필요하다. 따라서 이진탐색이 항상 효율적인 것이 아니다.
그러나 여러번 배열을 탐색하는 경우라면 한 번은 정렬해두면 장기적인 이득을 얻을 수 있어 좋다. 따라서 상황에 따라 a. 버블정렬+이진탐색을 쓸지, b. 선형탐색을 쓸지 선택해야 한다.

4. Ω(n^2)

1. 도출

자료가 이미 정리된 상태라도 버블정렬은 무식하게 루프돌면서 다 비교한다. 따라서 최적의 경우에도 Ω(n^2)이다.

2. 빅 오메가 정리

Ω(n^2) : bubble sort
Ω(n log n)
Ω(n)
Ω(log n)
Ω(1) : linear search, binary search

3. Ω(n)

만약 운좋게 자료가 다 정리되어서 첫번째 회차에 한 번도 교환이 발생하지 않았다면 정렬을 멈추는 알고리즘을 도입한다고 하자. 그렇게 되면 컴퓨터는 자료를 n-1회 검사하고 정렬을 끝낼 것이므로 이 때 버블정렬의 최적의 경우의 작업수는 Ω(n)이 된다.

5. 선택 정렬 (Selection Sort)

1. 정의

선택정렬 은 가장 작은 값을 찾아 선택한 후 왼쪽의 값과 교환하는 과정을 반복해서 정렬하는 방법이다.
선택정렬은 알고리즘이 단순하며, 사용할 수 있는 메모리가 제한적인 경우에 사용시 성능상의 이점이 있다.

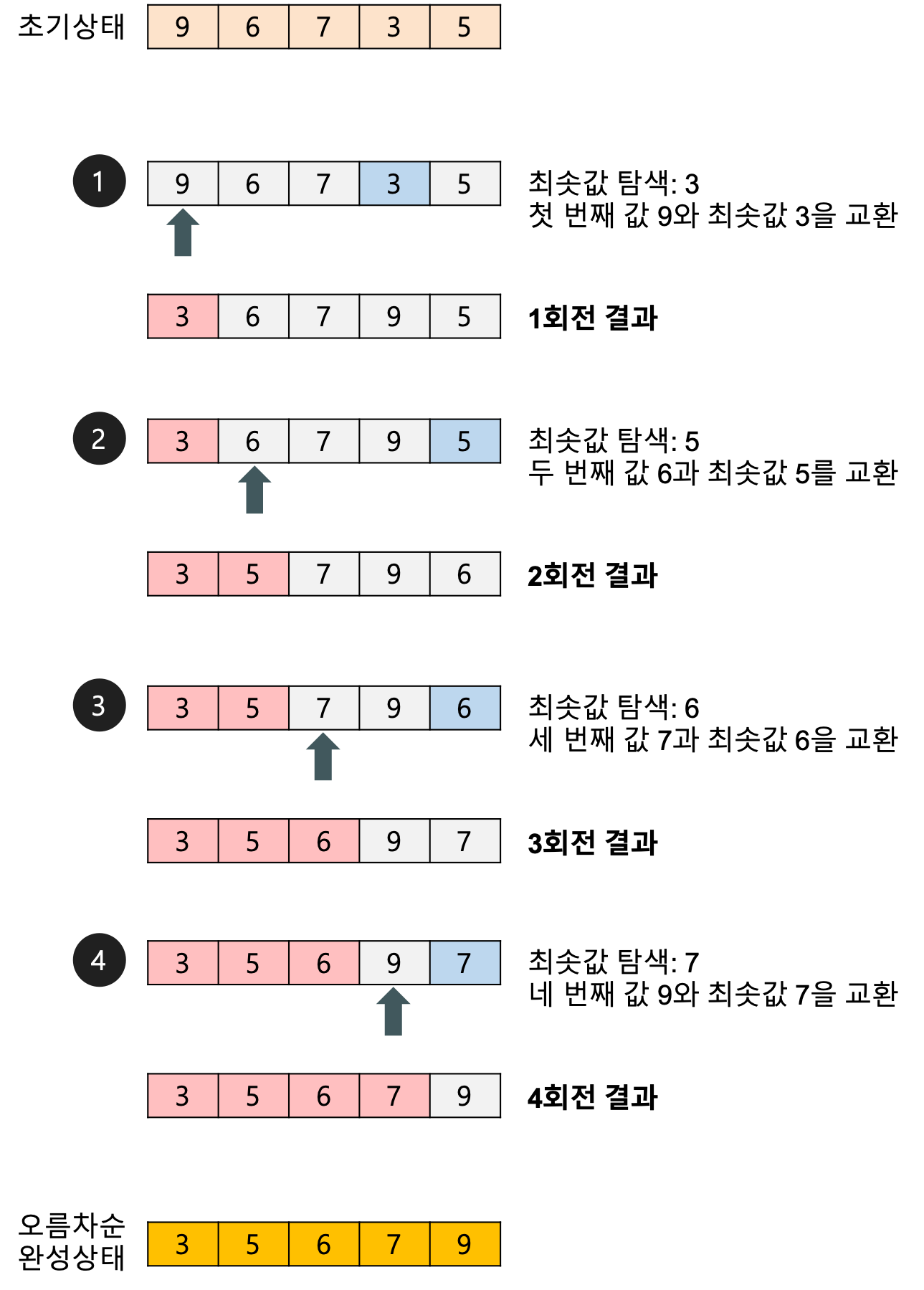
For i from 0 to n-1
	Find smallest item between i'th item and last item
	Swap smallest item with i'th item

2. O(n^2)

n + n-1 + ... + 2 + 1 = n(n+1) / 2
= n^2/2 + 1/2
= O(n^2)

:pushpin: 시간복잡도 Θ(n^2)인 정렬 알고리즘 중에서 선택 정렬은 버블 정렬보다 항상 우수하다.

3. Ω(n^2)

4. 생각해보기

:bulb: 선택정렬을 더 효율적으로 바꿀 수 있을까요?
1. 이중 선택 정렬: 한 번의 탐색에서 최솟값과 최댓값을 같이 찾는 방법이다. 탐색 횟수가 절반으로 줄어든다.
2. 한 번의 탐색 때 동일한 값이 있다면 함께 정렬하는 방법: 같은 값이 많을수록 유용하다.

6. 정렬 알고리즘의 실행시간

1. 실행시간의 상한

O(n^2) : bubble sort, selection sort
O(n log n)
O(n) : linear search
O(log n) : binary search
O(1)

2. 실행시간의 하한

Ω(n^2) : bubble sort, selection sort
Ω(n log n)
Ω(n)
Ω(log n)
Ω(1) : linear search, binary search

3. 버블정렬의 실행시간의 하한 단축하기

For i from 0 to n-2 until no swaps
	For j from 0 to n-2-i
		If j'th and j+1th elements out of order
			Swap them

안쪽 루프에서 교환이 하나도 일어나지 않을 때(즉, 이미 정렬이 잘 된 경우) 루프를 멈추도록 하는 것이다. 따라서 최선의 경우 처음부터 정렬이 되어있다면 n번만 작업하면 정렬이 완료됨 => Ω(n)

4. 생각해보기

:bulb: 선택정렬의 실행시간의 하한도 더 단축시킬 수 있을까?
불가능하다.

7. 재귀 (Recursion)

:pushpin: 핵심 개념: 재귀, 스택
:pushpin: 재귀는 재용이가 회사에서 자주 사용하는 알고리즘이다.

재귀 : 함수가 본인 스스로를 호출해서 사용하는 것. 또는 쉽게 설명하자면 눈에 보이는 혹은 가상의 물체의 구조를 그 물체 자체를 이용해서 설명하는 것.
ex. 3단짜리 피라미드는 2단짜리 피라미드에 한 줄을 추가해서 만든 것이다.
주의: 시작점에 대해서는(ex. 0단짜리 피라미드) 내가 직접 이건 특별한 경우이므로 아무것도 하지 말고 재귀적으로 자기 자신을 호출하지 않도록 처리해야 한다.

1. 반복문을 중첩해서 피라미드 출력하기

피라미드 모양은 이렇다

#include  <cs50.h>
#include  <stdio.h>

void  draw(int  h);

int  main(void)
{
	// 피라미드 높이 입력받아 저장
	int  height = get_int("Height: ");
	// 피라미드 그리기
	draw(height);
}

void  draw(int  h)
{
	for (int  i = 1; i <= h; i++)
	{
		for (int  j = 1; j <= i; j++)
		{
			printf("#");
		}
		printf("\n");
	}
}

2. 재귀를 사용해 피라미드 그리기

1. 재귀함수의 구조

1. 함수를 종료하는 조건
2. 함수 호출 (ex. draw(h-1)) 
3. 함수 동작문
// 1, 2, 3의 순서는 경우에 따라 바뀔 수 있지만 대략적으로 이렇게 생겨먹음.

2. 코드 그림으로 설명

3. 피라미드 그리기 코드

#include  <cs50.h>
#include  <stdio.h>

void  draw(int  h);

int  main(void)
{
	int  height = get_int("Height: ");
	draw(height);
}

void  draw(int  h)
{
	// 높이가 0이라면 함수 종료(아무것도 출력하지 않음)
	if(h == 0)
	{
		return;			//return의 역할
	}
	
	// h-1층 피라미드를 그린다.
	draw(h-1);

	// 폭이 h인 피라미드 한 층을 밑에 그린다.
	for (int  i = 0; i < h; i++)
	{
		printf("#");
	}
	printf("\n");
}

이렇게 재귀를 사용하면 중첩 루프를 사용하지 않고도 하나의 함수로 동일한 작업을 수행할 수 있다.

:pushpin: 함수에서 return의 역할
4.1. 부록에 따로 정리해놨으니 꼭 보기

3. 재귀를 이용해 시그마값 구하기

$\displaystyle\sum_{i=1}^{n} t_i$

int sigma(int n)
{
	if (n <= 0)
	{
		return;
	}
	return (n + sigma(n-1));
}

4. 스택

재귀함수에서 동일한 함수를 계속해서 호출할 대마다 함수를 위한 메모리가 계속해서 할당된다. 이 때 사용되는 메모리를 스택이라고 한다.
스택에는 함수에서 사용되는 변수와 같은 값들이 저장된다. 재귀함수를 이용하면 함수가 종료되지 않은 상태에서 함수가 새로 호출되는데, 이 때마다 새로운 값들이 스택에 저장된다. 따라서 잘못하면 스택 공간이 초과되어 프로그램 충돌이 발생(Stackoverflow)한다.
메모리 사용 문제 때문에 재귀는 유의해서 사용해야하지만, 특정 자료구조(트리 및 연결리스트)를 다룰 때 유용하게 사용된다.

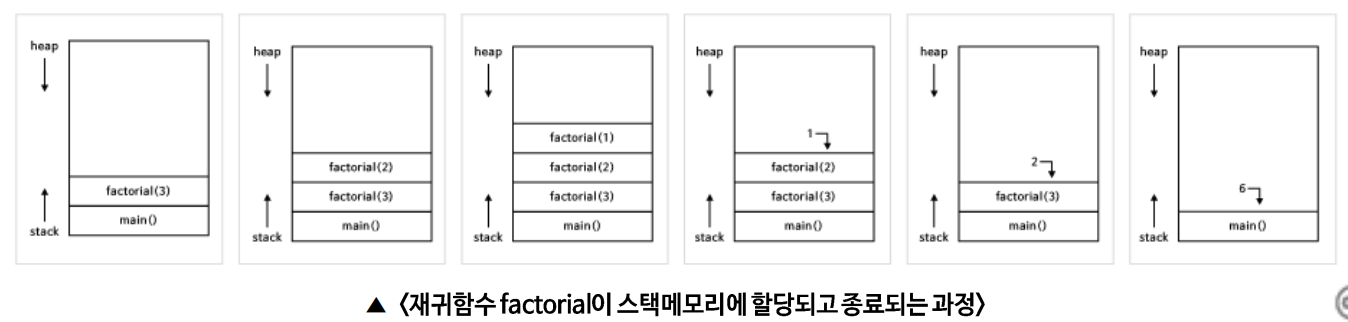
5. 생각해보기

:bulb: 반복문을 쓸 수 있는데도 재귀를 사용하는 이유는 무엇일까요?
재귀함수는 반복문보다 코드를 더 간결하게 쓸 수 있어 다른사람이 읽었을 때 이해하기 쉽고, 유지보수도 쉽기 때문이다.

Recursion and Looping

반복문 vs 재귀 부분 요약

속도: 반복문이 우수 (재귀는 반복적으로 함수를 호출하기 때문에 느리다)
메모리: 반복문이 우수 (재귀는 함수를 호출할 때마다 각 함수의 local variables와 parameters를 저장하기 위해 function call stack을 사용해야 함. 이는 메모리에 많은 부담을 주며 잘못하면 스택오버플로우가 생길수도 있음)
코드: 재귀가 우수 (반복문은 코드가 길고 복잡해서 장기적으로 유지보수할 때 불리하다 - 코드를 읽고 이해하기 불편함)
반복문을 쓸지 재귀를 쓸지 판단하는 기준
- Design Complexity: 가장 중요한 기준. 만약 문제가 복잡하고 반복적인 것이면 Divide and conquer 방법으로 접근한다. 이 때 재귀함수를 사용하는 것이 유리함
- 사용하는 언어: JAVA, C, Python(imperative language)에서는 반복문이 더 유리함(재귀의 경우 함수를 계속 새로 호출하기 때문). C와 같은 functional language에서는 재귀함수가 더 유리함(tail recursion같은 특정 재귀함수가 사용된 경우 함수를 반복해서 호출하지 않기 때문).
- 시간/공간 제약: 제약이 있는 상태라면 반복문을 사용하는게 나음
- 코드 유지보수: 재귀가 나음

8. 병합정렬 (Merge sort)

:pushpin: 핵심개념: 병합 정렬, 분할 정복

1. 병합정렬 원리

병합정렬 은 원소가 한 개가 될 때까지 계속해서 반으로 나누다가 다시 합쳐나가며 정렬을 하는 방식. 이 과정은 재귀적으로 구현된다.

1. 의사코드

// Base case: hard code
If only one item
	Return
// 정렬
Else
	Sort left half of items
	Sort right half of items
	Merge sorted halves

2. 동작 방식

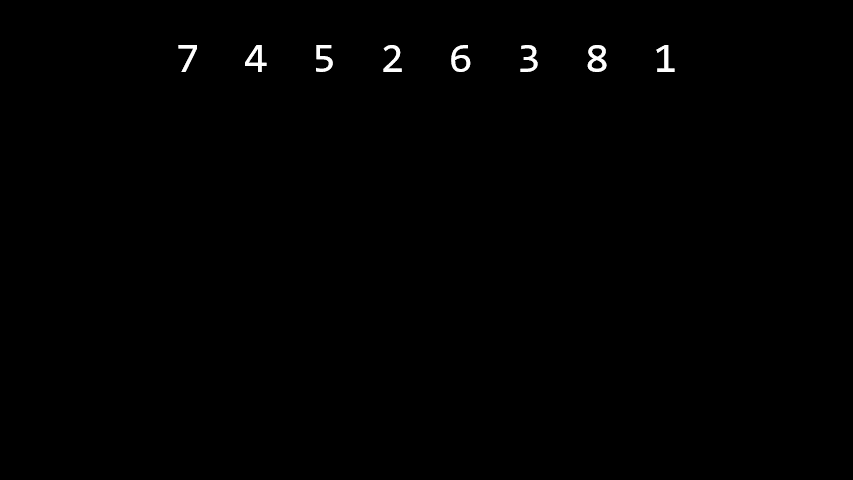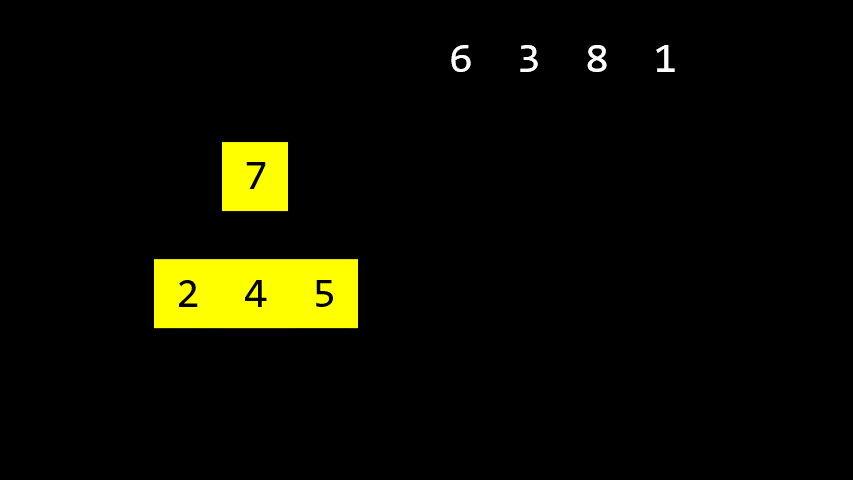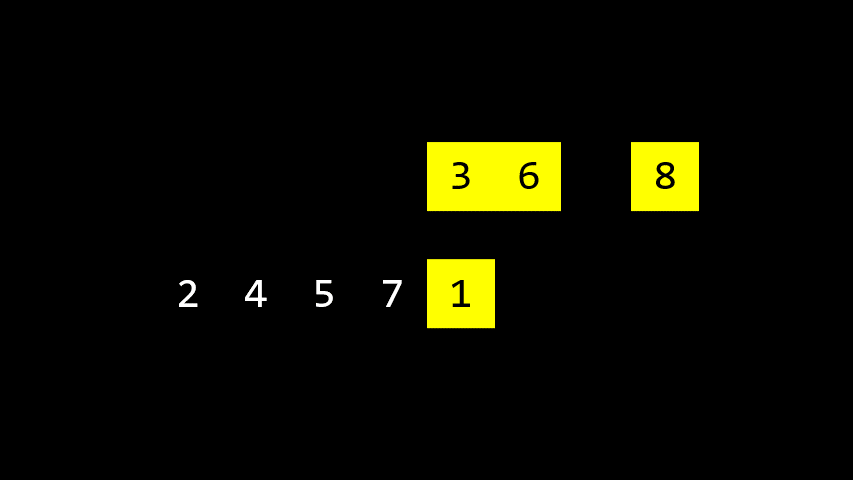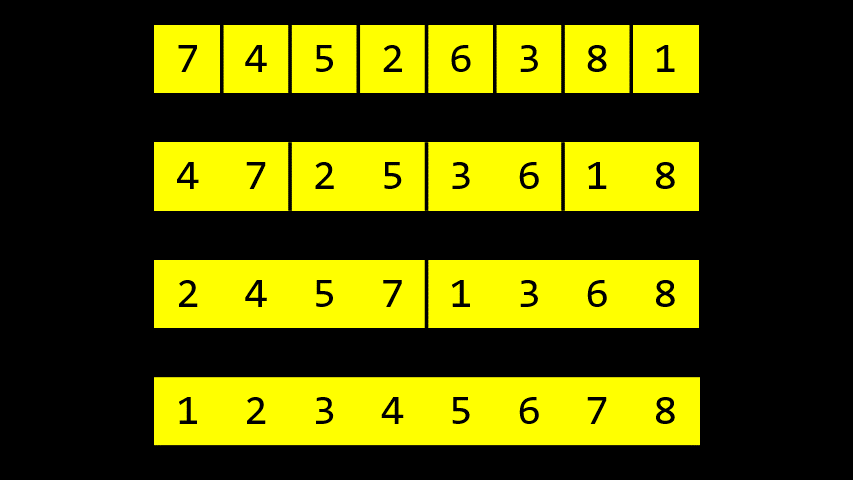애니메이션에서 볼 수 있듯이, 나눠진 배열을 병합할 때는 가장 작은 원소를 왼쪽에 배치하는 방식으로 병합한다.

2. O(n log n)

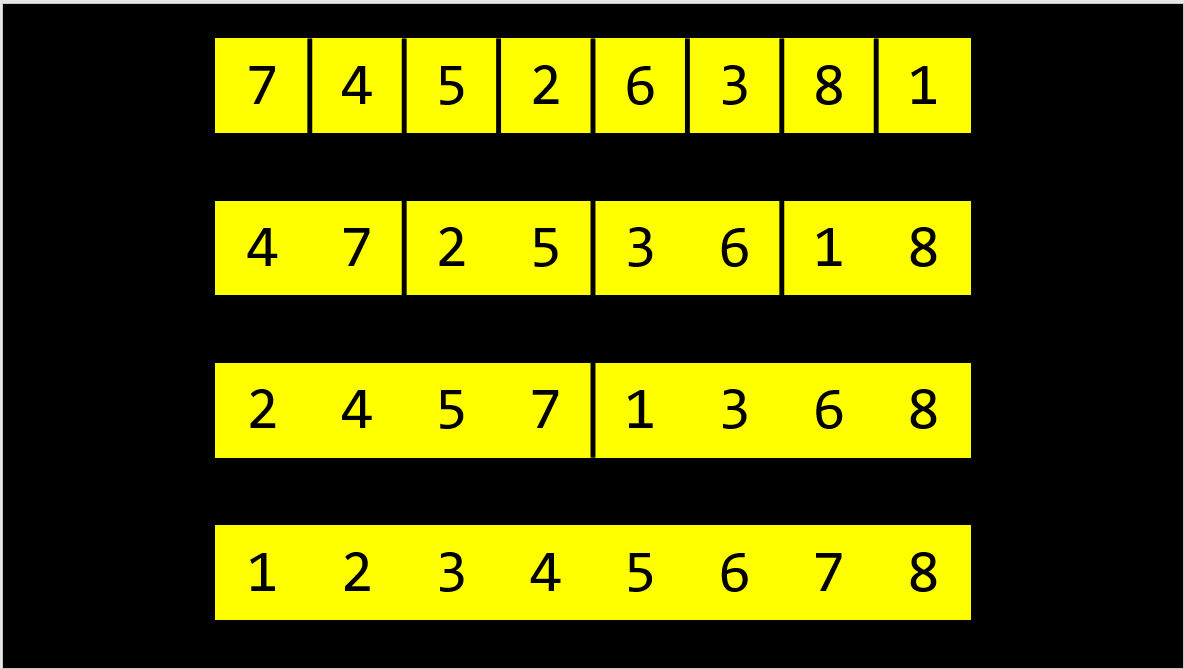
주어진 배열은 총 $log_2 8$ 회 나누어진다.
각 단계에서 컴퓨터는 총 8개의 원소를 검사해 대소관계를 따지고 순서대로 정렬한다.
따라서 작업의 횟수는 총 $8 log_2 8$ 회다.

일반화하면 병합정렬의 실행시간의 상한은 O(n log n)이다.

3. Ω(n log n)

병합정렬의 실행시간의 하한 역시 Ω(n log n)이다. 병합정렬은 숫자들이 이미 정렬되었는지 여부에 관계 없이 나누고 병합하기 때문이다. (무식함)

4. Θ(n log n)

어떤 알고리즘의 실행시간의 상한 = 하한일 때 Θ 사용하면 됨

Θ(n^2) : selection sort
Θ(n log n) : merge sort
Θ(n)
Θ(log n)
Θ(1)

cf. 버블정렬: 정렬이 다 된 상태라면 버블정렬을 중단한다는 조건문을 추가한다면 실행시간의 하한은 Ω(n^2)에서 Ω(n)으로 바뀐다.

5. 분할 정복 (Divide and Conquer)

1. 개념

분할 정복은 여러 알고리즘의 기본이 되는 해결방법으로, 크고 방대한 문제를 조금씩 나눠가면서 용이하게 풀 수 있는 문제 단위로 나눈 다음, 그것들을 다시 합쳐서 해결하는 개념이다. 대표적으로는 퀵소트나 병합정렬이 있다.

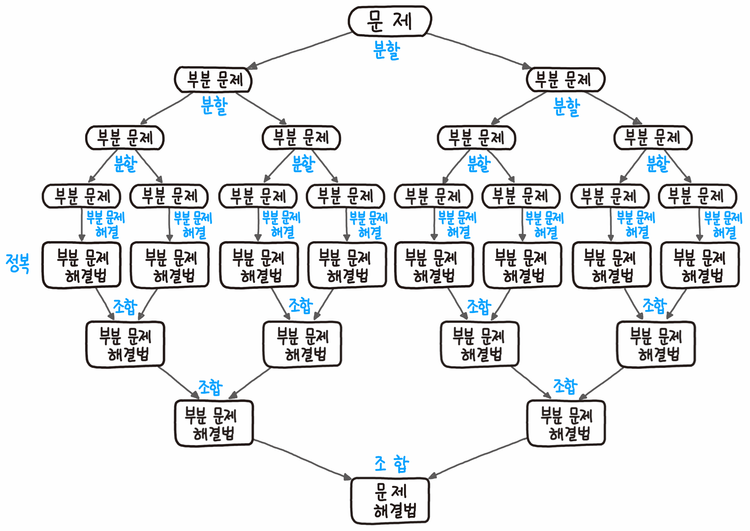
2. 적용 방식

function F(x)
	if F(x)가 간단
		return
	else
		x를 x1, x2로 분할
		F(x1), F(x2) 호출
		return [F(x1)와 F(x2) 병합한 값]

"F(x)가 간단"이라는 조건을 만족할 때까지 문제를 쪼개서 값을 구하고 병합해 전체 문제를 해결하는 개념이다.

3. 장단점

1. 장점

병렬적으로 문제를 해결하는데 강점이 있음

2. 단점

재귀적 함수 호출로 인한 오버헤드가 발생하며, 스택에 다양한 데이터를 보관하고 있어야 하므로 스택 오버플로우가 발생하거나, 과도한 메모리 사용을 하게 됨
"F(x)가 간단"이라는 조건이 무엇이냐에 따라 알고리즘의 퍼포먼스가 생각보다 꽤 차이나게 됨 (Base case를 정의하는 것의 난해함)

6. 생각해보기

:bulb: 병합 정렬을 선택 정렬이나 버블 정렬과 비교했을 때 장단점은?
참고

	선택정렬	버블정렬	병합정렬
공간복잡도	O(1)	O(1)	O(n)
최선 시간복잡도	Θ(n^2)	Θ(n^2)	Θ(nlogn)

cf. 공간복잡도 프로그램을 실행시킨 후 완료하는 데 필요로 하는 자원 공간의 양을 뜻한다. `총 공간 요구 = 고정 공간 요구 + 가변 공간 요구` (시간과 공간은 반비례함 -> 알고리즘의 척도는 시간복잡도를 위주로 판단한다. 즉, 시간복잡도만 괜찮다면 공간복잡도는 어느 정도 이해해줌)

장점: 선택정렬, 버블정렬과 비교했을 때 작업속도가 빠르다
단점: 더 많은 메모리를 사용한다

Elenaljh

이전 포스트

3.1. 추가내용

다음 포스트

4. 알고리즘

CS50

4. 알고리즘

1. 검색 알고리즘

1. 선형 검색 (Linear search)

2. 이진 검색 (Binary search)

2. 알고리즘 표기법

1. Big-O

2. Big Ω

3. 생각해보기

3. 선형 검색 (Linear Search)

1. 정수형 자료에서 선형검색하기

2. 문자열 자료에서 선형검색하기

3. 새로운 자료형으로 구조체 (structure) 정의하기

4. 생각해보기

4. 버블 정렬 (Bubble Sort)

1. 정의

2. 의사 코드

3. O(n^2)

1. 버블정렬 작업 수

2. 빅오 정리

4. Ω(n^2)

1. 도출

2. 빅 오메가 정리

3. Ω(n)

5. 선택 정렬 (Selection Sort)

1. 정의

2. O(n^2)

3. Ω(n^2)

4. 생각해보기

6. 정렬 알고리즘의 실행시간

1. 실행시간의 상한

2. 실행시간의 하한

3. 버블정렬의 실행시간의 하한 단축하기

4. 생각해보기

7. 재귀 (Recursion)

1. 반복문을 중첩해서 피라미드 출력하기

2. 재귀를 사용해 피라미드 그리기

1. 재귀함수의 구조

2. 코드 그림으로 설명

3. 피라미드 그리기 코드

3. 재귀를 이용해 시그마값 구하기

4. 스택

5. 생각해보기

8. 병합정렬 (Merge sort)

1. 병합정렬 원리

1. 의사코드

2. 동작 방식

2. O(n log n)

3. Ω(n log n)

4. Θ(n log n)

5. 분할 정복 (Divide and Conquer)

1. 개념

2. 적용 방식

3. 장단점

1. 장점

2. 단점

6. 생각해보기

3.1. 추가내용

4.1. 부록

0개의 댓글