벡터와 매트릭스(Vectors and Matrics)

• 데이터사이언스와 선형대수의 관계를 알 수 있다.
• 벡터에 대한 기본 계산을 할 수 있다.
• 매트릭스에 대한 기본 계산을 할 수 있다.
• 단위행렬과 같은 특별한 매트릭스를 이해하고, 행렬식(determinant)이나 역행렬(inverse)을 계산할 수 있다.
• Numpy를 사용하여 기본 선형대수 계산을 할 수 있다.

• Matrix Calculation

  • Matrix multiplication
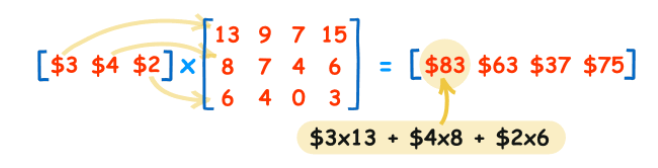
  • Determinant (행렬식) 행렬식 계산 코드 : np.linalg.det()
    
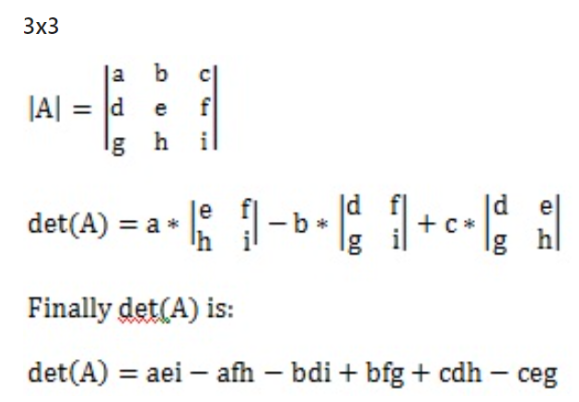
  • Dimensionality (차원) 매트릭스의 행과 열의 숫자를 차원이라 표현한다. dimension 코드 : df.ndim
    
  • Transpose (전치) 매트릭스의 행과 열을 바꾸는 것을 의미한다. transpose 코드 : df.T
    
  • Inverse (역행렬) 매트릭스의 나눗셈은 선형대수에 존재하지 않기 때문에 역행렬을 곱해줌 행렬에 역행렬을 곱하면 단위 매트릭스가 된다. inverse 코드 : np.linalg.inv() ❓역행렬이 존재하지 않는 경우 행렬식이 0인 경우 = 2개의 행 혹은 열이 선형의 관계를 이루고 있음 → 매트릭스의 행과 열이 선형의 의존 관계가 있는 경우 매트릭스의 행렬식은 0이다.
    • Identity (단위 매트릭스) Diagonal 매트릭스( 대각선 부분에만 값이 있고 나머지는 전부 0인 행렬) 중에서, 모든 값이 1인 경우
      
    • Symmetric (대칭) 대각선을 기준으로 위 아래의 값이 대칭인 경우

• Saclar / Vector

  • Scalar : 단일 숫자로 실수와 정수 모두 가능하다.

    

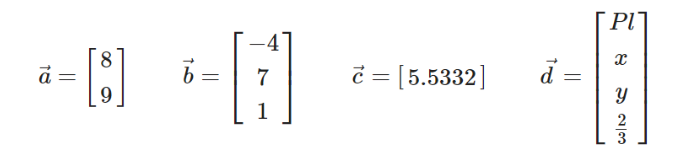
  • Vector : n차원의 벡터는 컴포넌트라 불리는 n개의 원소를 가지는 순서를 갖는 모음

    (컴포넌트는 스칼라로 간주되지 않음)

    

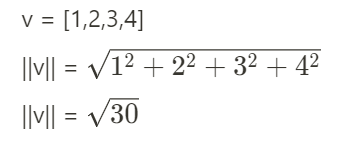
    위 벡터들은 각각 2, 3, 1, 4차원을 가진다.

    벡터의 길이는 벡터의 차원 수와 동일하다.

    • Vector의 크기( Magnitude, Norm, Length)

      벡터의 크기는 단순히 길이에 지나지 않는다. ( 크기를 표현할 때 || ||를 사용)

      v = [1,2,3,4]

      ||v|| = $\sqrt{1^2 + 2^2 + 3^2 + 4^2}$

      ||v|| = $\sqrt{30}$
      

    • Vector의 내적 (dot product)

      두 벡터의 내적은 각 구성요소를 곱한 뒤 합한 값과 같다.
      
      벡터 내적 코드 : `np.dot()`

      ❓np.dot() 과 np.matmul() 차이

    1. 3차원 이상의 다차원 배열에서 연산을 수행하는 방법이 다르다.
    2. np.dot() 은 배열과 스칼라의 곱을 계산하지만 np.matmul() 은 오류가 발생한다.