2014~2018년 미국 지역사회설문조사 (ACS, American Community Survey) 5년 추정치에서 수집한 '미국 인구조사국' 데이터로 진행해보겠습니다.

데이터 불러오기

CREATE TABLE 테이블명 만들기 ( 각 컬럼들의 타입);
-> COPY , FROM , WITH 데이터 불러오기
-> SELECT 확인해보기

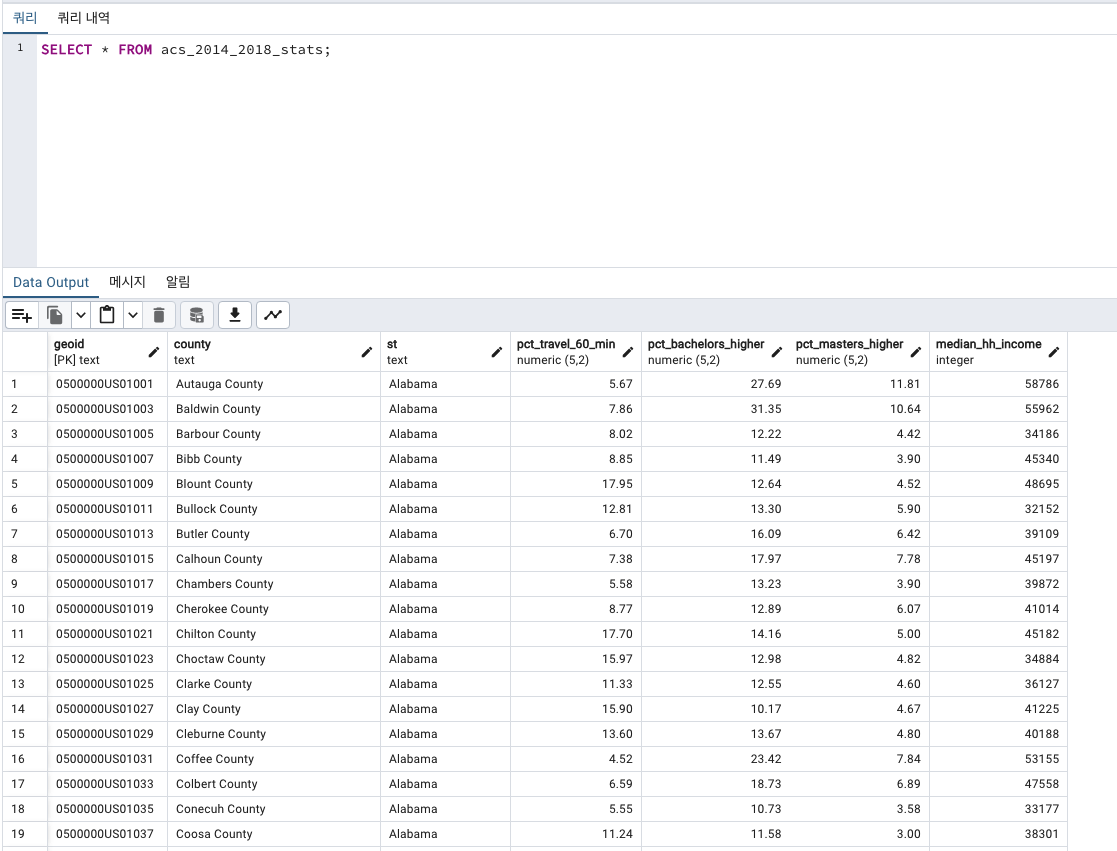
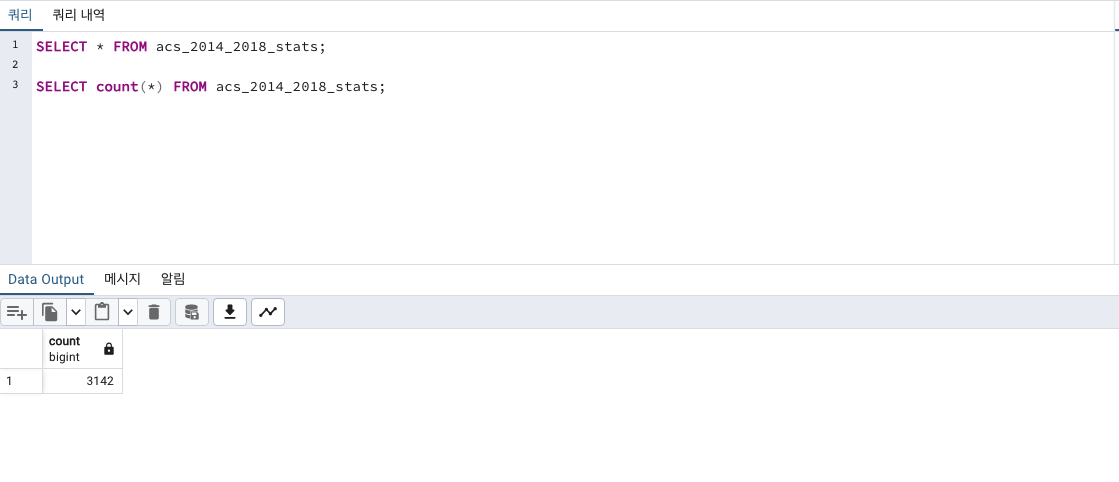
총 3142개의 rows의 데이터가 있는 테이블이 생성되었습니다.

상관관계 corr(y,x)

상관관계란 하나의 변수가 다른 변수의 변화에 영향을 미치는 정도를 의미하여, 두 변수간의 관계를 측정합니다.

최대 양의 관계 +1과 최대 음의 관계 -1 사이로 구해집니다.

하나가 증가하면 나머지도 증가한다. => 최대 +1 까지이며 보통 0.6정도면 강함
하나가 증가하면 나머지도 감소한다. => 최소 -1 까지이며 보통 -0.6정도면 강함
0 에 가까울수록 두 변수는 연관성이 없다는 뜻입니다.

SELECT corr(y컬럼, x컬럼)
FROM 테이블명

• geoID
• county 마을
• st 도시
• pct_travel_60_min 출퇴근시간 60분이상 근로자 비율
• pct_bachelors_higher 학사이상 25세이상 인구 비율
• pct_masters_higher 석사이상 25세이상 인구 비율
• median_hh_income 2018년도 기준 카운티의 평균 가계 소득(중앙값)

median_hh_income 가 y가 되어 소득에 미치는 영향력이 큰 변수들을 알아보겠습니다.

SELECT corr(median_hh_income, pct_bachelors_higher) 
FROM acs_2014_2018_stats;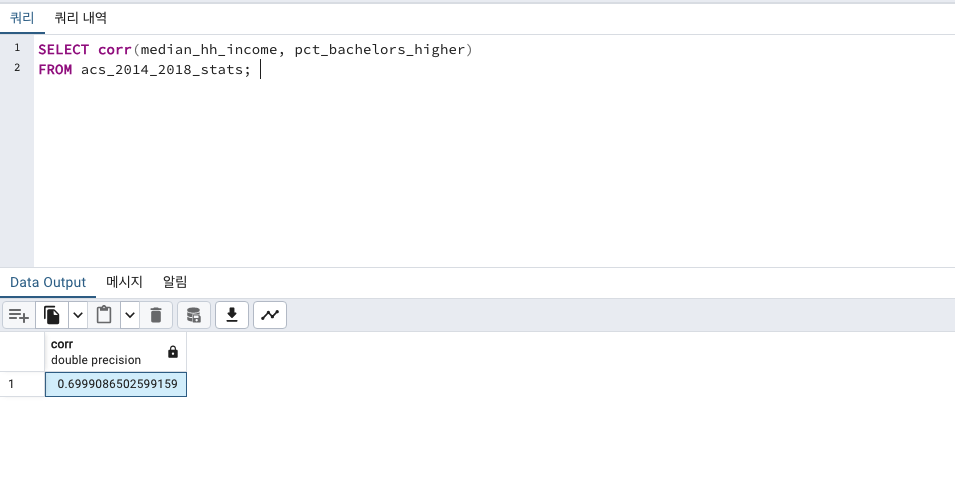 

0.69는 꽤나 강한 양의 상관관계를 미치는 수치입니다.

이제 y를 고정시키고 x값에 나머지 변수들도 집어넣어보겠습니다.

SELECT 
	corr(median_hh_income, pct_bachelors_higher) as pct_bach, 
	corr(median_hh_income, pct_masters_higher) as pct_mast, 
	corr(median_hh_income, pct_travel_60_min) as pct_60min
FROM acs_2014_2018_stats;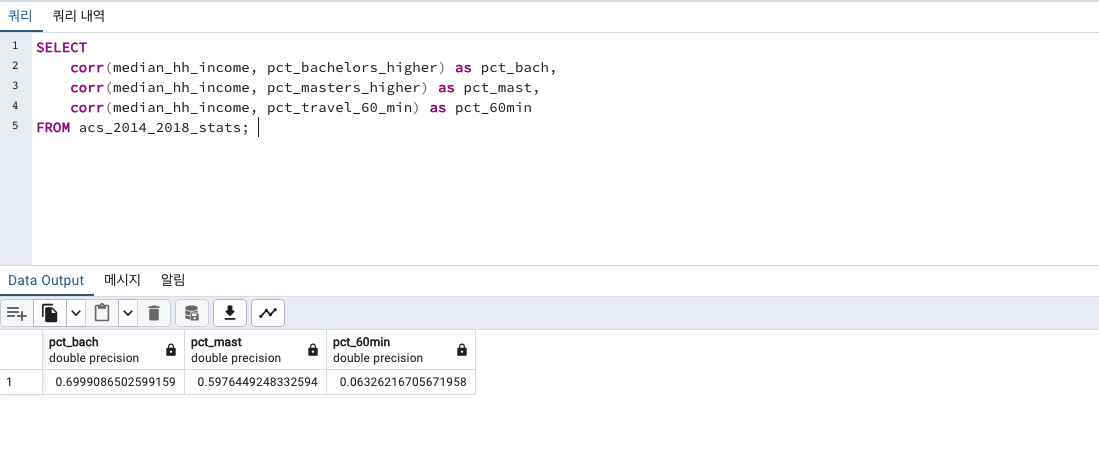 

세 가지 변수 모두 꽤나 높게 나왔습니다.

round()함수를 통해 반올림해보겠습니다.
참고로 round()함수는 integer로 가장 가까운 정수로 반올림해버립니다. ::numeric으로 타입변환하여 소수점도 나오게 해줍니다.

SELECT 
	round(corr(median_hh_income, pct_bachelors_higher)::numeric,2) as pct_bach, 
	round(corr(median_hh_income, pct_masters_higher)::numeric,2) as pct_mast, 
	round(corr(median_hh_income, pct_travel_60_min)::numeric,2) as pct_60min
FROM acs_2014_2018_stats;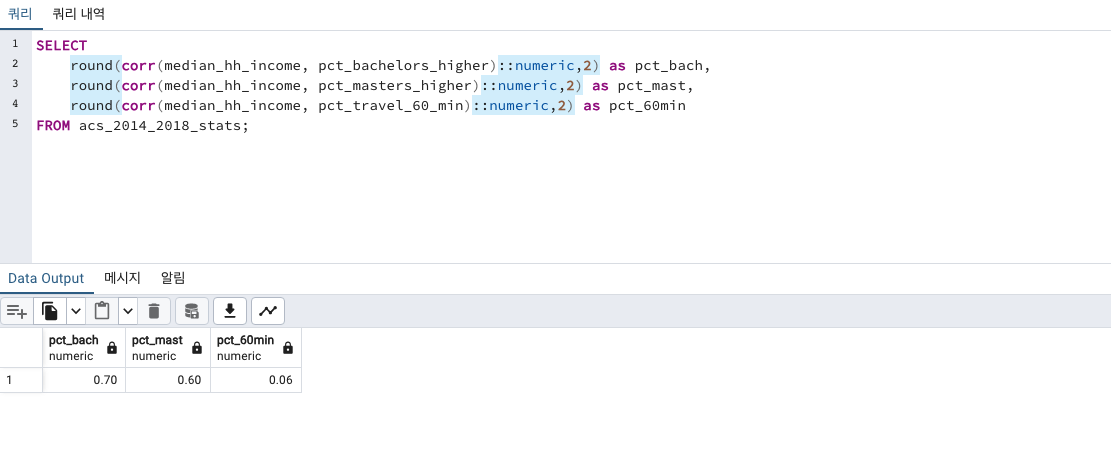 

상관계수 r

상관분석함수 corr(y,x)를 통해 나오는 수치가 상관계수 r 입니다.

회귀분석 예측 regr_

상관분석은 두 변수 간의 연관성을 파악하는데 사용되고,
회귀분석은 한 변수가 다른 변수에 미치는 영향을 분석하고 예측하는데 사용합니다.

선의 기울기와 절편

기울기와 절편은 두 변수 간의 선형 관계를 정의하고 평균 변화율을 추정하는 데 사용할 수 있습니다. 기울기 크기가 클수록 선이 더 경사지고 변화율이 더 커집니다.

기울기 = x가 1증가할때마다 y가 얼마나 증가하는지의 값
절편 = x가 0으로 회귀선이 y축을 교차할때 y축의 값

회귀방정식 y=b(비율)+a

학사 학위이상을 가진 사람들의 비율이 30%일때, 예상되는 가계 소득 중간값
y = 회귀기울기(30) + 절편
y = slope값(30) + y의 intercept값

기울기slope와 절편intercept

regr_slope(y변수, x변수)
regr_intercept(y변수, x변수)

SELECT 
	regr_slope(median_hh_income, pct_bachelors_higher), 
	regr_intercept(median_hh_income, pct_bachelors_higher)
FROM acs_2014_2018_stats; 



-- round( 내용 ::numeric, 2) 함수로 
SELECT 
	round(regr_slope(median_hh_income, pct_bachelors_higher)::numeric, 2), 
	round(regr_intercept(median_hh_income, pct_bachelors_higher)::numeric, 2) 
FROM acs_2014_2018_stats;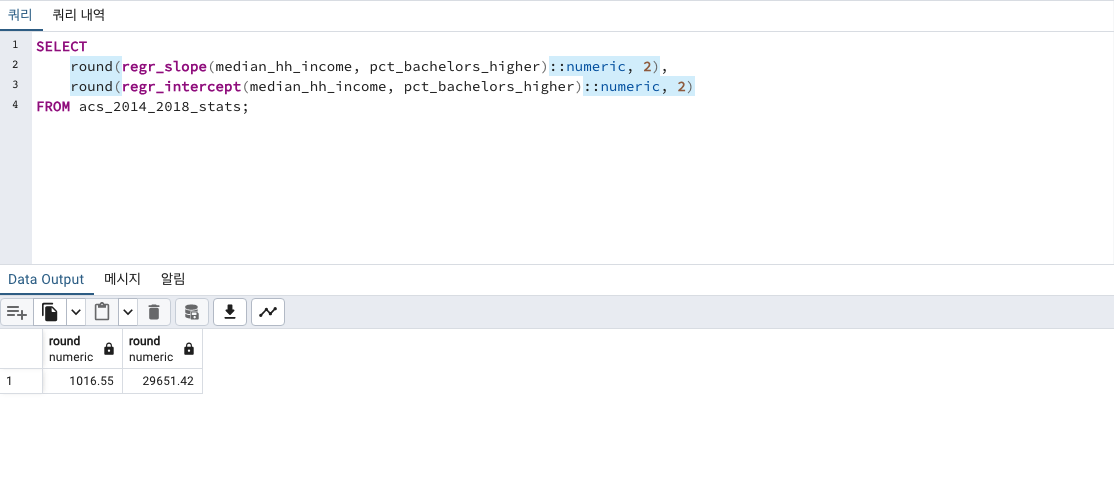 

slope값은 x(학사 학위비율)이 1 증가할때마다 y(평균 가구 소득)이 1016만큼 증가할 수 있습니다.

intercept값은 x(학사 학위비율)이 0으로 회귀선이 y축을 교차할때 y축 값이 29651인 값입니다.

회귀방정식 y=b(비율)+a

학사 학위이상을 가진 사람들의 비율이 30%일때, 예상되는 가계 소득 중간값
y = (회귀기울기 x 30) + 절편
y = (slope값 x 30) + y의 intercept값

여기서 y = 1016.55*30 + 29651.42 = 약 60147.92 입니다.

25세이상인구의 30%가 학사학위이상인 카운티에서 해당 카운티의 평균 가계 소득은 약 60147 달러입니다.

결정계수 r2

상관계수 r

상관분석함수 corr(y,x)를 통해 나오는 수치가 상관계수 r 입니다.

결정계수 r2

상관계수로 구한 모델이 얼마나 잘 예측하고 설명하는지를 의미합니다. (0~1사이로서, 1에 가까울수록 좋음)

• R2값은 종속 변수의 변동 중에서 회귀 모형이 설명하는 비율을 나타냅니다.
• 예를 들어, R2값이 0.8이라면 종속 변수의 변동 중 80%가 회귀 모형으로 설명됩니다.
• 회귀 모형의 설명력을 평가하고, 모델이 데이터를 얼마나 잘 적합시키는지를 파악하는 데에 사용됩니다.

regr_r2(y변수, x변수)

반올림 round(내용 ::numeric, 2)

SELECT 
	regr_r2(median_hh_income, pct_bachelors_higher) as pct_bach, 
	regr_r2(median_hh_income, pct_travel_60_min) as pct_60min
FROM acs_2014_2018_stats; 


-- round()로 반올림 
SELECT 
	round(regr_r2(median_hh_income, pct_bachelors_higher)::numeric,2) as pct_bach, 
	round(regr_r2(median_hh_income, pct_travel_60_min)::numeric,2) as pct_60min
FROM acs_2014_2018_stats;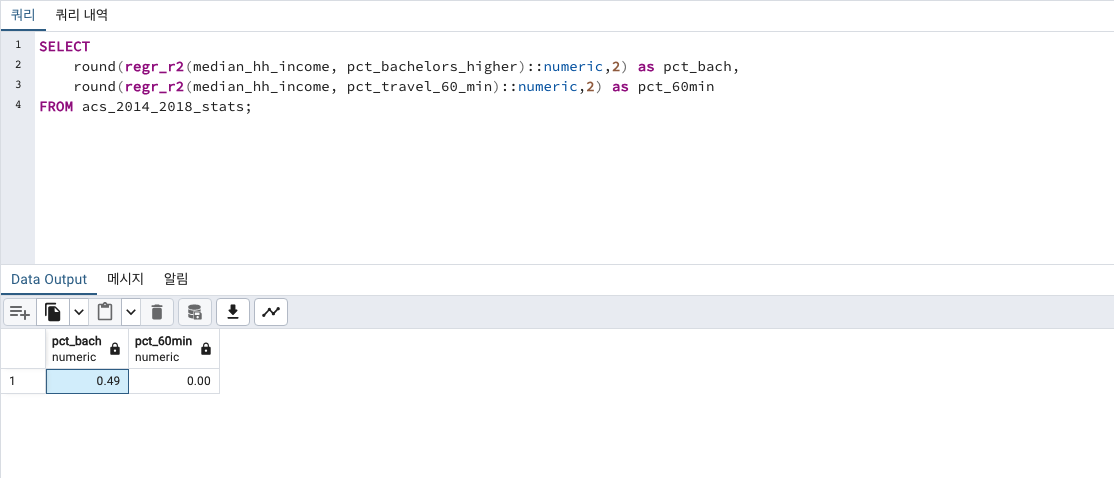 

중간가구소득변동의 약 49%가 학사 학위이상을 가진 사람들의 비율입니다.
중간가구소득변동과 출퇴근시간이 60분인이상의 사람들의 연관성은 없는걸로 보여집니다.

순위매기는 윈도우함수

계산을 수행하는 함수를 윈도우함수 WINDOW FUNTION 이라고 합니다.

현재 행을 기준으로 행 집합에서 계산을 수행하는 윈도우 함수

• RANK() OVER (ORDER BY 컬럼명 )
• DENSE_RANK() OVER (ORDER BY 컬럼명)

RANK()와 DENSE_RANK()

SELECT 
	median_hh_income, 
	st, 
	county , 
	RANK()OVER (ORDER BY median_hh_income DESC), 
	DENSE_RANK() OVER (ORDER BY median_hh_income DESC)
FROM acs_2014_2018_stats;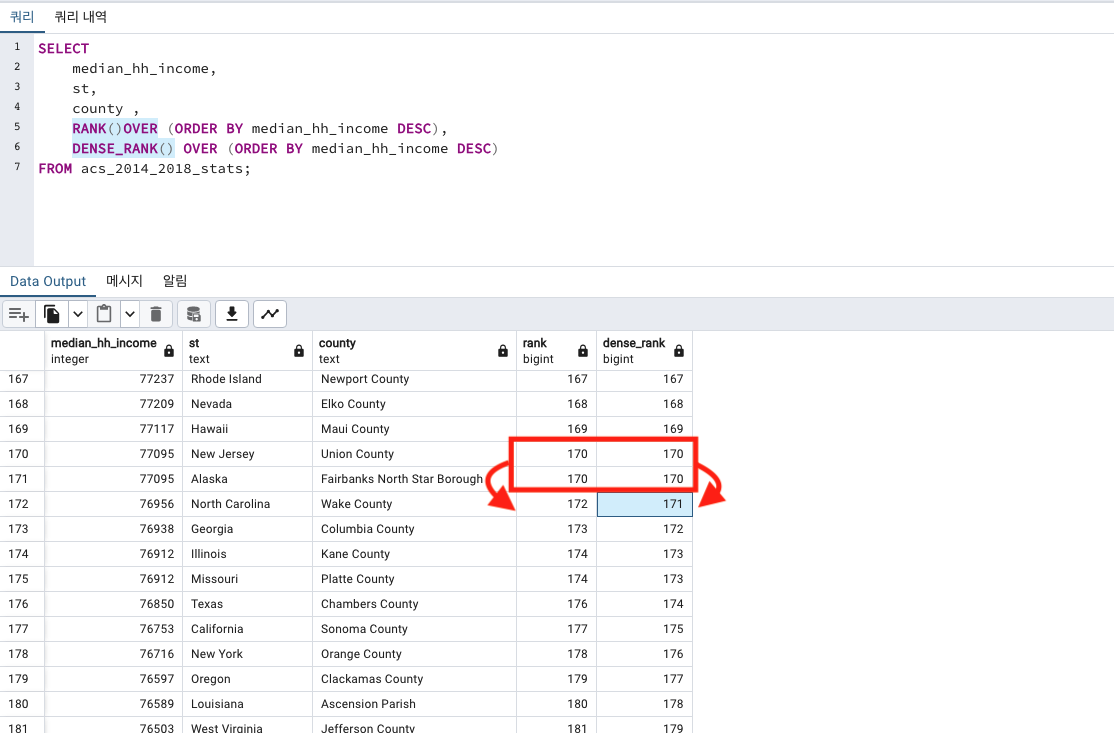 

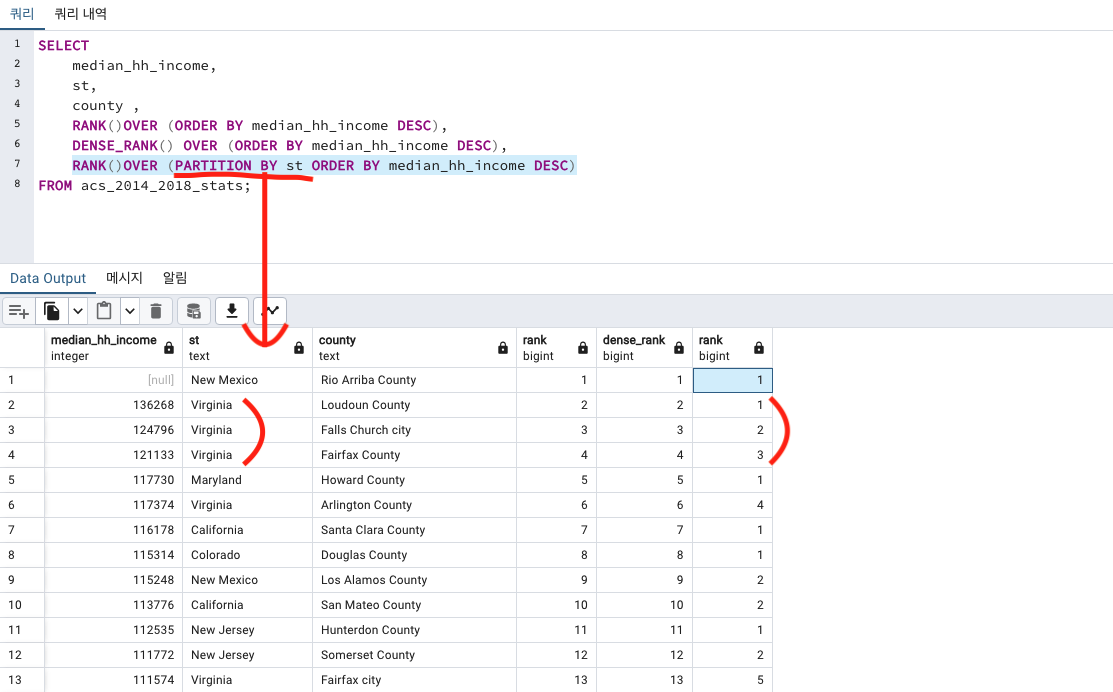
그룹내 순위 PARTITION BY 추가

기존 RANK()OVER (ORDER BY median_hh_income DESC) 에
PARTITION BY를 추가해줍니다.

RANK()OVER (PARTITION BY st ORDER BY median_hh_income DESC)

SELECT 
	median_hh_income, 
	st, 
	county , 
	RANK()OVER (ORDER BY median_hh_income DESC), 
	DENSE_RANK() OVER (ORDER BY median_hh_income DESC),
	RANK()OVER (PARTITION BY st ORDER BY median_hh_income DESC)
FROM acs_2014_2018_stats;