문제
그래프를 DFS로 탐색한 결과와 BFS로 탐색한 결과를 출력하는 프로그램을 작성하시오. 단, 방문할 수 있는 정점이 여러 개인 경우에는 정점 번호가 작은 것을 먼저 방문하고, 더 이상 방문할 수 있는 점이 없는 경우 종료한다. 정점 번호는 1번부터 N번까지이다.
입력
첫째 줄에 정점의 개수 N(1 ≤ N ≤ 1,000), 간선의 개수 M(1 ≤ M ≤ 10,000), 탐색을 시작할 정점의 번호 V가 주어진다. 다음 M개의 줄에는 간선이 연결하는 두 정점의 번호가 주어진다. 어떤 두 정점 사이에 여러 개의 간선이 있을 수 있다. 입력으로 주어지는 간선은 양방향이다.
출력
첫째 줄에 DFS를 수행한 결과를, 그 다음 줄에는 BFS를 수행한 결과를 출력한다. V부터 방문된 점을 순서대로 출력하면 된다.
예제 입력
4 5 1
1 2
1 3
1 4
2 4
3 4예제 출력
1 2 4 3
1 2 3 4예제 입력2
5 5 3
5 4
5 2
1 2
3 4
3 1예제 출력2
3 1 2 5 4
3 1 4 2 5예제 입력3
1000 1 1000
999 1000예제 출력3
1000 999
1000 999해설
입력받은 값으로 인접 행렬 그래프를 만든 후 bfs와 dfs를 구현했다.
인접행렬행성
값으로 주어진 노드와 간선으로 인접행렬을 만든다.
예를 들어
4 5 1
1 2
1 3
1 4
2 4
3 4가 주어진다면 이런 그래프를 의미한다
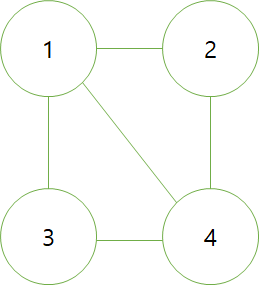
또한 이 그래프를 인접행렬로 표현하면

bfs
bfs는 Queue로 구현한다
Queue는 FIFO 특징이 있기때문에 너비우선을 탐색할때 유용하다.
v->Queue에 v를 넣는다 ->
Queue에서 값을 꺼낸다(v) -> 그래프에서 v와 연결된 값(값이 1)을 탐색(i)-> i를 Queue에 넣는다 -> Queue에서 값을 꺼낸다
의 반복
dfs
dfs는 Stack 으로 구현한다
Stack은 FILO 특징이 있기 때문에 깊이우선탐색에 유리하다.
v->Stack에 v를 넣는다 ->
Stack에서 값을 찾는다(v) -> 그래프에서 v와 연결된 값(값이 1)을 탐색(i)-> i를 Stack에서 넣는다 -> Stack에서 값을 찾는다
의 반복
여기서 중요한 것은 peek으로 값을 보기만 한다는 것이다.
깊이우선탐색이기 때문에 돌아가야할 값을 기억해야하기 때문에 값을 꺼내진 않는다
flag를 이용해서 값에 찾아갈 수 있는 노드가 없으면 pop을 이용해 stack에서 꺼낸다.
전체 풀이
public class Main {
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt(); //정점 개수
int m = sc.nextInt(); //간선 개수
int v = sc.nextInt(); //간선
int[][] arr = new int[n + 1][n + 1];
//인접행렬 구현
for (int i = 0; i < m; i++) {
int j = sc.nextInt();
int k = sc.nextInt();
arr[j][k] = 1;
arr[k][j] = 1;
}
dfs(arr, v);
System.out.println();
bfs(arr, v);
}
//bfs : Queue
public static void bfs(int[][] a, int v) {
Queue<Integer> q = new LinkedList<>();
boolean[] c = new boolean[a.length + 1];
int n = a.length - 1;
q.add(v);
c[v] = true;
while (!q.isEmpty()) {
v = q.poll();
System.out.print(v + " ");
for (int i = 1; i <= n; i++) {
if (a[v][i] == 1 && !c[i]) {
q.add(i);
c[i] = true;
}
}
}
}
//dfs : Stack
public static void dfs(int[][] a, int v) {
Stack<Integer> stack = new Stack<>();
boolean[] c = new boolean[a.length + 1];
int n = a.length - 1;
stack.push(v);
c[v] = true;
System.out.print(v + " ");
while (!stack.isEmpty()) {
int vv = stack.peek();
boolean flag = false;
for (int i = 1; i <= n; i++) {
if (a[vv][i] == 1 && !c[i]) {
stack.push(i);
System.out.print(i + " ");
c[i] = true;
flag = true;
break;
}
}
if (!flag) {
stack.pop();
}
}
}
}
