알기쉬운 알고리즘 4주차(2) - 그래프(BFS, DFS)

hjseo-dev·2021년 8월 17일

BFS DFS python 그래프 알고리즘

Python 알고리즘

목록 보기

13/13

📍 그래프

연결되어 있는 정점와 정점간의 관계를 표현할 수 있는 자료구조,

노드(Node): 연결 관계를 가진 각 데이터를 의미합니다. 정점(Vertex)이라고도 합니다.
간선(Edge): 노드 간의 관계를 표시한 선.
인접 노드(Adjacent Node): 간선으로 직접 연결된 노드(또는 정점)

      로제 - 사나
             ⎜       
      제니 - 르탄

르탄이는 연결 관계를 가진 데이터, 노드입니다!
르탄과 제니는 간선으로 연결되어 있습니다.
르탄과 로제는 인접 노드 입니다!

✏️ 표현방식

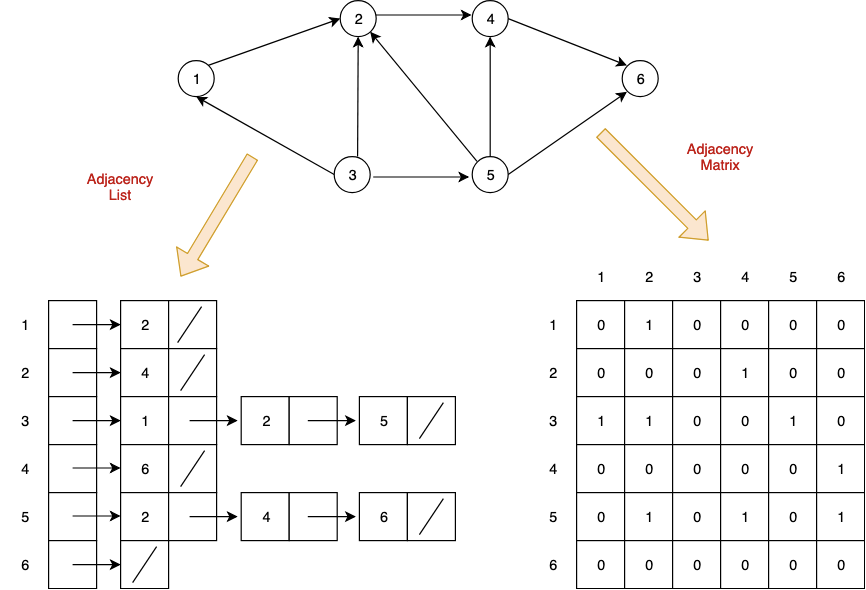
1) 인접 행렬(Adjacency Matrix): 2차원 배열로 그래프의 연결 관계를 표현
2) 인접 리스트(Adjacnecy List): 링크드 리스트로 그래프의 연결 관계를 표현


      2 - 3
          ⎜       
      0 - 1
      
1. 이를 인접 행렬, 2차원 배열로 나타내면 다음과 같습니다!
  0  1  2  3
0 X  O  X  X
1 O  X  O  X
2 X  O  X  O
3 X  X  O  X

이걸 배열로 표현하면 다음과 같습니다!
graph = [
    [False, True, False, False],
    [True, False, True, False],
    [False, True, False, True],
    [False, False, True, False]
]

2. 이번에는 인접 리스트로 표현해보겠습니다!
인접 리스트는 모든 노드에 연결된 노드에 대한 정보를 차례대로 다음과 같이 저장합니다.

0 -> 1
1 -> 0 -> 2
2 -> 1 -> 3
3 -> 2

이를 딕셔너리로 표현하면 다음과 같습니다!
graph = {
    0: [1],
    1: [0, 2]
    2: [1, 3]
    3: [2]
}

위 방식의 차이는 시간 VS 공간 입니다!

인접 행렬으로 표현하면 즉각적으로 0과 1이 연결되었는지 여부를 바로 알 수 있습니다. 그러나, 모든 조합의 연결 여부를 저장해야 되기 때문에 $O(노드^2)$ 만큼의 공간을 사용해야 합니다.
인접 리스트로 표현하면 즉각적으로 연결되었는지 알 수 없고, 각 리스트를 돌아봐야 합니다. 따라서 연결되었는지 여부를 알기 위해서 최대 $O(간선)$ 만큼의 시간을 사용해야 합니다. 대신 모든 조합의 연결 여부를 저장할 필요가 없으니 $O(노드 + 간선)$ 만큼의 공간을 사용하면 됩니다.

💡 DFS & BFS

DFS : 자료의 검색, 트리나 그래프를 탐색하는 방법. 한 노드를 시작으로 인접한 다른 노드를 재귀적으로 탐색해가고 끝까지 탐색하면 다시 위로 와서 다음을 탐색하여 검색한다.
BFS : 한 노드를 시작으로 인접한 모든 정점들을 우선 방문하는 방법

ex) 알파고
대국에서 발생하는 모든 수를 계산하고 예측해서 최적의 수를 계산해내기 위해
모든 수를 전부 탐색해야 합니다.
DFS 와 BFS 는 그 탐색하는 순서에서 차이가 있습니다.
DFS 는 끝까지 파고드는 것이고, BFS 는 갈라진 모든 경우의 수를 탐색해보고 오는 것이 차이점입니다.

📍 DFS

DFS 는 끝까지 파고드는 것이라, 그래프의 최대 깊이 만큼의 공간을 요구합니다. 따라서 공간을 적게 씁니다. 그러나 최단 경로를 탐색하기 쉽지 않습니다.
DFS는 Depth First Search 라고 했습니다!

💡 실행과정

DFS 의 반복 방식은 방문하지 않은 원소를 계속해서 찾아가면 됩니다!
DFS 의 반복 방식은 방문하지 않은 원소를 계속해서 찾아가면 됩니다!

즉, DFS(node) = node + DFS(node와 인접하지만 방문하지 않은 다른 node) 로 반복하면 됩니다.

방문하지 않았다는 조건 => visited 라는 배열에 방문한 노드를 기록해두면 될 것 같습니다.

루트 노드부터 시작한다.
현재 방문한 노드를 visited 에 추가한다.
현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드에 방문한다.
2부터 반복한다.

현재 방문한 노드와 인접한 노드는 adjacent_graph[cur_node] 로 구할 수 있습니다! 방문하지 않은 걸 확인 하기 위해서는 visited_array 를 이용

✏️ 코드작성1 - 재귀함수

# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
    1: [2, 5, 9],
    2: [1, 3],
    3: [2, 4],
    4: [3],
    5: [1, 6, 8],
    6: [5, 7],
    7: [6],
    8: [5],
    9: [1, 10],
    10: [9]
}
visited = []

#1. 시작노드인 1 부터 탐색한다.
#2. 방문한 노드를 visited_array에 추가한다.
#3. 현재 방문한 노드와 인접한 노드중 방문하지 않은 노드에 방문한다.

def dfs_recursion(adjacent_graph, cur_node, visited_array):
    visited_array.append(cur_node)
    for adjacent_node in adjacent_graph:
        if adjacent_node not in visited_array:
            dfs_recursion(adjacent_graph, adjacent_node, visited_array)

    return


dfs_recursion(graph, 1, visited)  # 1 이 시작노드입니다!
print(visited)  # [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 이 출력되어야 합니다!

재귀함수를 통해서는 무한정 깊어지는 노드가 있는 경우 에러가 생길 수 있어 다른 방법을 써봐야 한다!

✏️ 코드작성2 - 스택

💡 구현방법

루트 노드를 스택에 넣습니다.
현재 스택의 노드를 빼서 visited 에 추가한다.
현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 스택에 추가한다.
2부터 반복한다.
스택이 비면 탐색을 종료한다.

방문하지 않았다는 조건 visited 라는 배열에 방문한 노드를 기록

# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
    1: [2, 5, 9],
    2: [1, 3],
    3: [2, 4],
    4: [3],
    5: [1, 6, 8],
    6: [5, 7],
    7: [6],
    8: [5],
    9: [1, 10],
    10: [9]
}

#시작노드를 스택에 넣는다.
#현재 스택의 노드를 빼서 visited에 추가한다
#현재 방문한 노드와 인접한 노드 중에서 방문하지 않은 노드를 스택에 추가한다

def dfs_stack(adjacent_graph, start_node):
    stack = [start_node]
    visited = []
    while stack:
        current_node = stack.pop()
        visited.append(current_node)
        for adjacent_node in adjacent_graph[current_node]:
            if adjacent_node not in visited:
                stack.append(adjacent_node)
    return visited


print(dfs_stack(graph, 1))  # 1 이 시작노드입니다!
# [1, 9, 10, 5, 8, 6, 7, 2, 3, 4] 이 출력되어야 합니다!

📍 BFS

BFS 는 현재 인접한 노드 먼저 방문해야 합니다.
이걸 다시 말하면 인접한 노드 중 방문하지 않은 모든 노드들을 저장해두고,
가장 처음에 넣은 노드를 꺼내서 탐색하면 됩니다.

가장 처음에 넣은 노드들..? → 큐를 이용하면 BFS 를 구현할 수 있습니다!

💡 구현방법

루트 노드를 큐에 넣습니다.
현재 큐의 노드를 빼서 visited 에 추가한다.
현재 방문한 노드와 인접한 노드 중 방문하지 않은 노드를 큐에 추가한다.
2부터 반복한다.
큐가딕 비면 탐색을 종료한다.

# 위의 그래프를 예시로 삼아서 인접 리스트 방식으로 표현했습니다!
graph = {
    1: [2, 3, 4],
    2: [1, 5],
    3: [1, 6, 7],
    4: [1, 8],
    5: [2, 9],
    6: [3, 10],
    7: [3],
    8: [4],
    9: [5],
    10: [6]
}

#시작노드를 큐에 넣는다.
#현재 큐의 노드를 빼서 visited에 추가한다
#현재 방문한 노드와 인접한 노드 중에서 방문하지 않은 노드를 큐에 추가한다

def bfs_queue(adj_graph, start_node):
    queue = [start_node]
    visited = []

    while queue:
        current_node = queue.pop(0)
        visited.append(current_node)
        for adjacent_node in adj_graph[current_node]:
            if adjacent_node not in visited:
                queue.append(adjacent_node)

    return visited


print(bfs_queue(graph, 1))  # 1 이 시작노드입니다!
# [1, 2, 3, 4, 5, 6, 7, 8, 9, 10] 이 출력되어야 합니다!