✏️ Graph
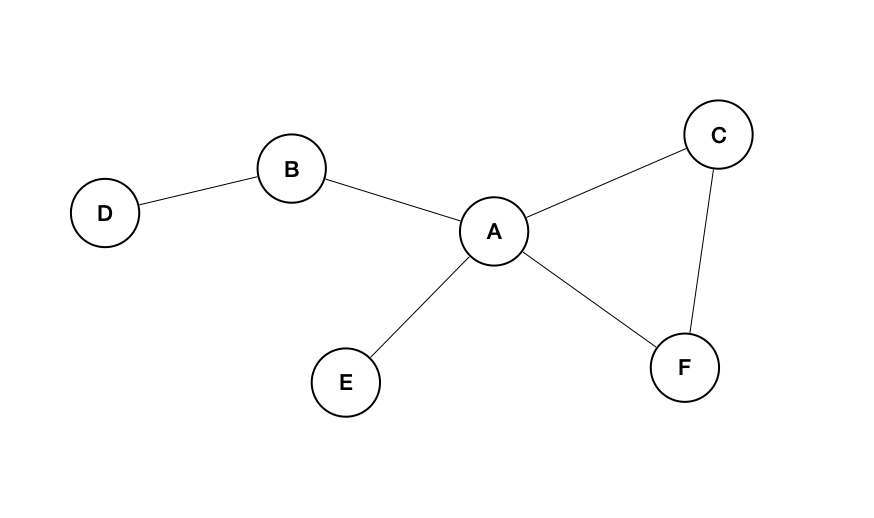
개념
- 정점(vertex)와 간선(edge)로 이루어진 자료구조
- 여러 개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조
특징
용어
- 정점 (vertex)
- 노드(node)라고도 함
- 데이터가 저장되는 그래프의 기본 원소
- 간선 (edge)
- 자기 루프 (self loop)
- 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우
- 다른 정점을 거치지 않음
- 사이클 (cycle)
- 한 정점에서 출발해 다시 해당 정점으로 돌아갈 수 있는 경우
- 시작 정점 = 끝 정점
- 단순 회로 (Simple cycle)
- 인접 정점 (adjacent vertex)
- 하나의 정점에서 간선에 의해 직접 연결되어 있는 정점
종류
- 가중치 그래프 (weighted graph)
- 가중치(or 비용)를 갖는 간선으로 이루어진 그래프
- 비가중치 그래프 (unweighted graph)
- 무(방)향 그래프 (undirected graph)
- 완전 그래프 (complete graph)
- 임의의 두 정점에 대해 두 정점을 잇는 간선이 존재하는 그래프
- 완전 그래프는 정점 그래프
- N개의 정점을 갖는 무향 그래프
- 간선 개수 = N(N−1)/2
- N개의 정점을 갖는 유향 그래프
- 간선 개수 = N(N−1)
- 연결 그래프 (connected graph)
- 임의의 두 정점에 대해 경로가 존재하는 그래프
- 부분 그래프
- 어떤 그래프의 정점 집합의 부분 집합과 그에 속한 간선들로 이루어진 그래프
- 어떤 그래프의 간선 집합의 부분 집합과 그에 속한 정점들로 이루어진 그래프
- 트리 그래프
- 순환(cycle)을 갖지 않는 연결 그래프
- 임의의 두 정점에 대해 경로가 정확히 1개 존재
- 하나 이상의 정점을 가짐
- 임의의 간선을 제거한 그래프는 연결 그래프가 아님
구현
- 인접 : 두 정점을 바로 이어주는 간선이 있는 경우
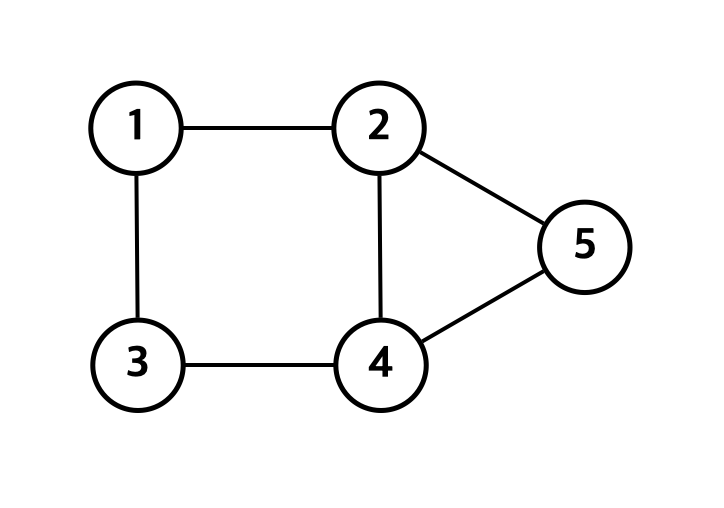
1️⃣ 간선 리스트 (Edge List)
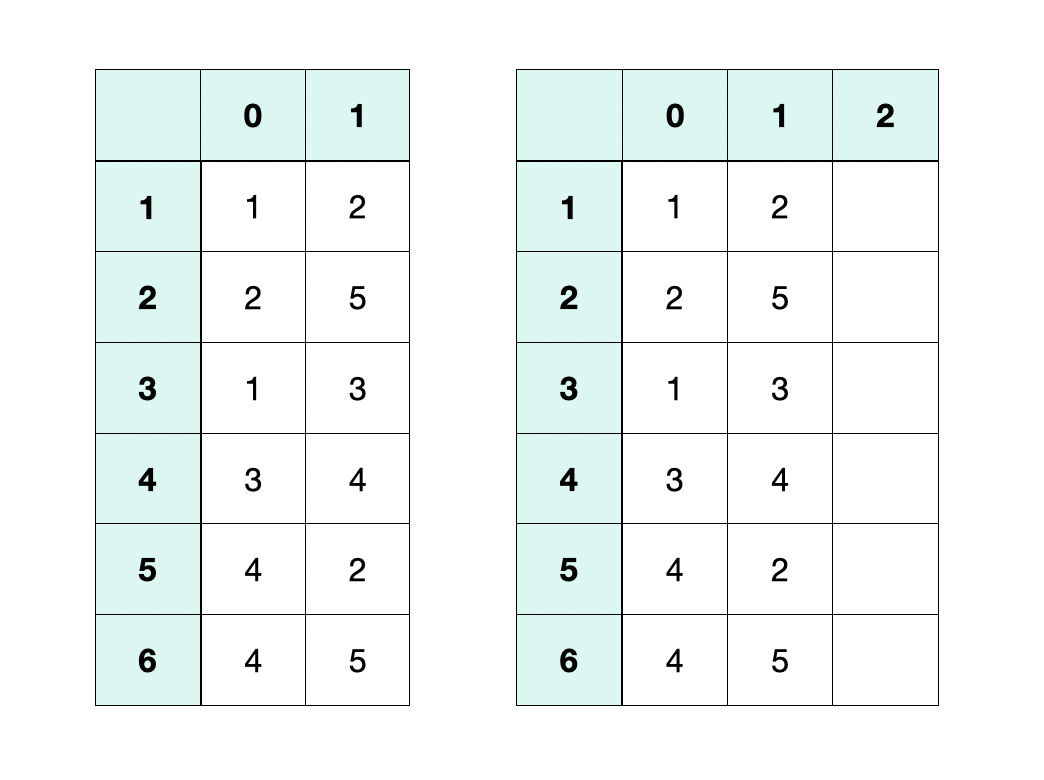
- 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 E∗2의 2차원 배열에 간선 정보 저장
- 어떤 두 정점 vi, vj를 연결하는 간선 ek=(vi,vj)에 대해서 A[k][0]=vi,A[k][1]=vj
- 가중치 그래프의 경우 배열의 3번째 열에 간선의 가중치 저장
2️⃣ 인접 행렬 (Adjacency Matrix)
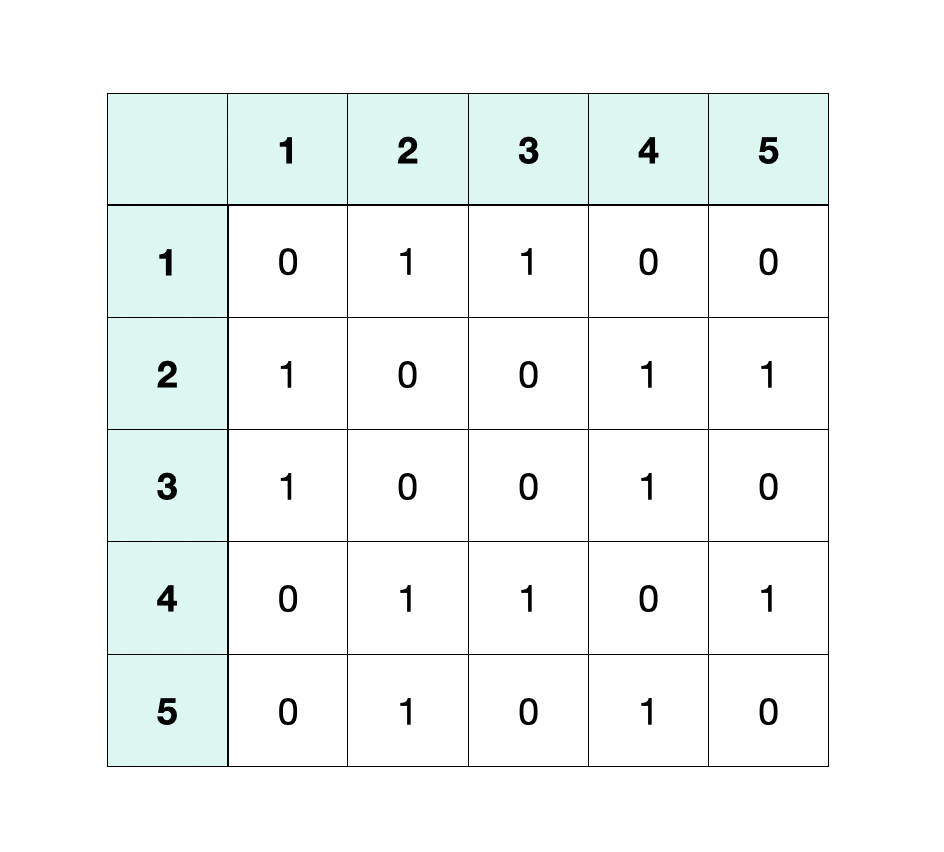
- 서로 다른 정점들이 인접한 상태인지를 표현한 행렬
- 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 V∗V의 2차원 배열(A)에 그래프 정보 저장
- 어떤 두 정점 vi, vj를 연결하는 간선 e=(vi,vj)이 존재하면 A[i][j]=1 (or 가중치), 존재하지 않으면 A[i][j]=0
- 두 정점 사이의 관계 유무 확인에 용이
- 가장 빠른 경로를 찾고자 할 때 주로 사용
- 정점, 간선 수가 많으면 사용하기 어려움
3️⃣ 인접 리스트 (Adjacent List)

- 각 정점이 어떤 정점과 인접하는지 리스트의 형태로 표현
- 정점의 개수가 V개, 간선의 개수가 E개인 그래프에 대해서 V개의 연결 리스트로 그래프 정보 저장
- 각 정점마다 하나의 리스트를 가짐
- 해당 리스트는 자신과 인접한 다른 정점을 담고 있음
- 메모리를 효율적으로 사용하고 싶을 때 사용
- 인접 행렬은 연결 가능한 모든 경우의 수를 저장하므로 상대적으로 메모리 차지 多
비교
| | 간선 리스트 | 인접 행렬 | 인접 리스트 |
|---|
| 공간 복잡도 | E | V2 | V+E |
| 시간 복잡도 - 정점의 부속 간선 | E | V | deg(Va) |
| 시간 복잡도 - 두 정점의 인접 여부 | E | 1 | min(deg(Va),deg(Vb)) |
| 시간 복잡도 - 정점 삽입 | 1 | V2 | 1 |
| 시간 복잡도 - 간선 삽입 | 1 | 1 | 1 |




