
Chapter 1~3 : 모스부호와 점자 → 점과 선/평면과 볼록으로 이뤄진 약속
Chapter 4~6 : 손전등과 릴레이 → 전기적인 특성
Chapter7
Chapter7에서는 앞에서 배운 적기적 특성을 어떻게 부호화 할 것인지 알아보기 전에 수를 세는 방법에 대해 설명한다.
숫자
우리가 사용하는 언어는 문화적 영향을 많이 받는 부호이다.
반면 숫자는 비교적 문화적 영향을 덜 받는 부호이다.
그러나 동시에 부호들 중 가장 추상화된 부호이기도 하다.
가령, 숫자 3을 보고 사람들은 3명, 3일, 3마리, 3번째 등 다양하게 연상한다
숫자가 발명된 이유
대부분의 역사학자는 경제활동을 위해 소유물을 세기 위해서 숫자를 사용했다고 말한다.
양 4마리를 표현하기 위해 양 4마리를 그리는 것보단 양을 하나만 그리고 흠집으로 개수를 표현하면 좋겠다는 생각을 떠올리게 된 것이다.
그러나 양이 마릿수가 많아지면 흠집으로 표현하는데 제한이 생기게 된다. 이런 문제를 해결하기 위해 방법을 떠올리다 발생한 것이 수 체계이다.
수 체계
대부분의 문명의 수 체계는 10(혹은 5)을 기반으로 하며, 이는 수를 셀 때 사용한 손가락이 10개이기 때문이다. 
이는 digit이라는 숫자를 뜻하는 단어의 어원이 손가락, 발가락이라는 점과 영어 five와 주먹 fist가 같은 어원을 가진다는 점에서 확인할 수 있다.
또한, 사람들은 10을 기반으로 하는 숫자에도 중요한 의미를 부여한다.
10년 - decade = 101
100년 - 세기(century) = 102
1000년 - 천년(millennium) = 103(thousand)
초기 수 체계 중 로마숫자 체계만이 지금까지 사용되고 있다.
EX) 시계 숫자판, 책 페이지 등
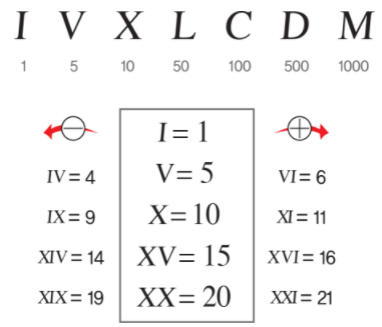
양 27마리를 로마숫자로 표기하면 다음과 같다.

흠집으로 수를 표현한 것보다는 좋아졌지만 로마숫자의 치명적인 단점은 곱셈과 나눗셈 연산에 적합하지 않다는 것이다.

오늘날의 수 체계
현대에서 사용하는 수 체계는 힌두-아라비아(인도-아라비아) 숫자로 인도에서 만들었으나 아라비아 수학자들에 의해 유럽에 전해졌다.
이전의 수 체계와 다른 힌두-아라비아 숫자의 특징은 다음과 같다.
- 숫자의 위치에 큰 의미를 부여한다
- "십"을 나타내기 위한 특별한 기호가 없다
- '0'이 존재한다
여기서 가장 중요한 특징은 0이다. 0을 통해 위치에 따른 표기법을 사용할 수 있게 되었고, 복잡한 연산도 수행할 수 있게 되었다.
위치에 따른 표기
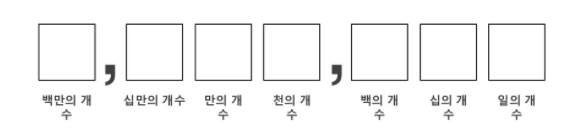
위의 7개의 박스로 0부터 9,999,999의 수를 표현할 수 있으며 각각의 자리는 10의 거듭제곱수에 해당한다.
1 = 100
10 = 101
100 = 102
...
1000000 = 106
이는 3과4 ,같은 모양의 수를 가지지만 위치에 따라 수의 차이를 둘 수 있게 된다. 따라서 위치에 따른 표기법으로 인해 다른 복잡한 연산도 가능해진다.
3 + 4 = 7
30 + 40 = (3+4) x 101 + 0 x 100 = 70
마지막으로 위치에 따른 표기법은 십진수 기반이 아닌 2진수 8진수 등에서도 유용하게 사용할 수 있다는 큰 장점이 있다.






