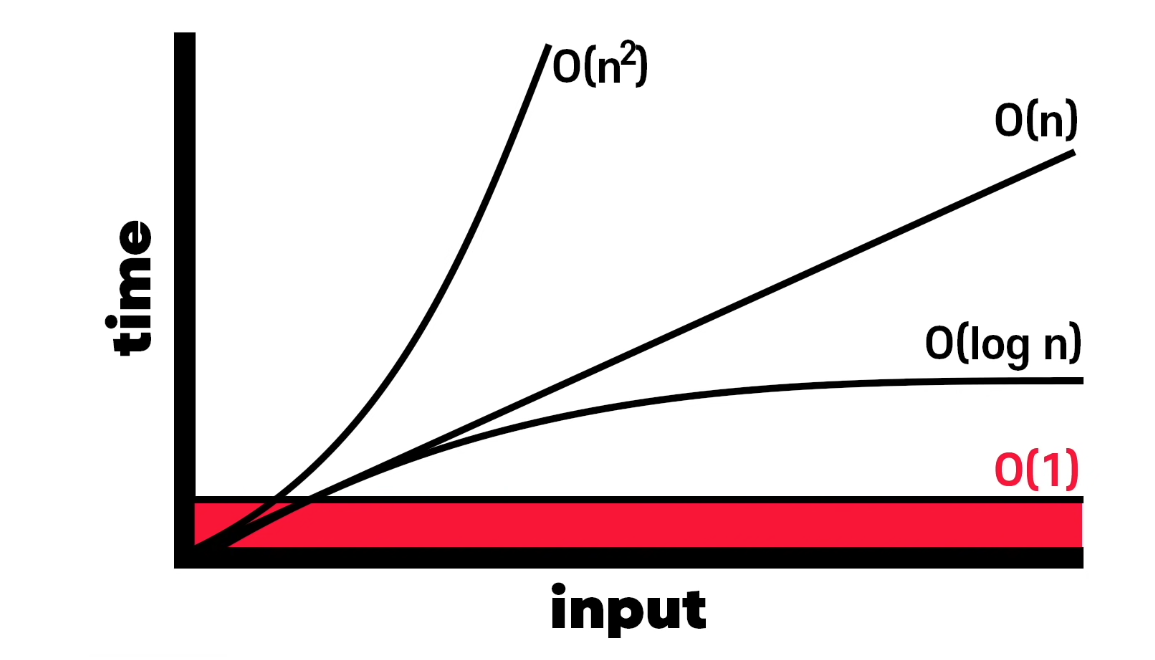
알고리즘 스피드의 표현법
- 알고리즘의 스피드는 완료까지 걸리는 절차의 수로 결정된다.
따라서 같은 작업을 수행하는데 5번 스텝만 필요한 알고리즘이 10개 스텝이 필요한 알고리즘 보다 훌륭한 알고리즘이다.
선형 알고리즘만 봐도 아이템이 10개인 경우 10번의 스텝이 필요하다.
따라서 input size 가 N 이라면
선형 알고리즘은 N 스텝이 요구된다고 할수 있다.
선형 검색의 시간복잡도는 O(N)을 갖는다고 할수 있다.
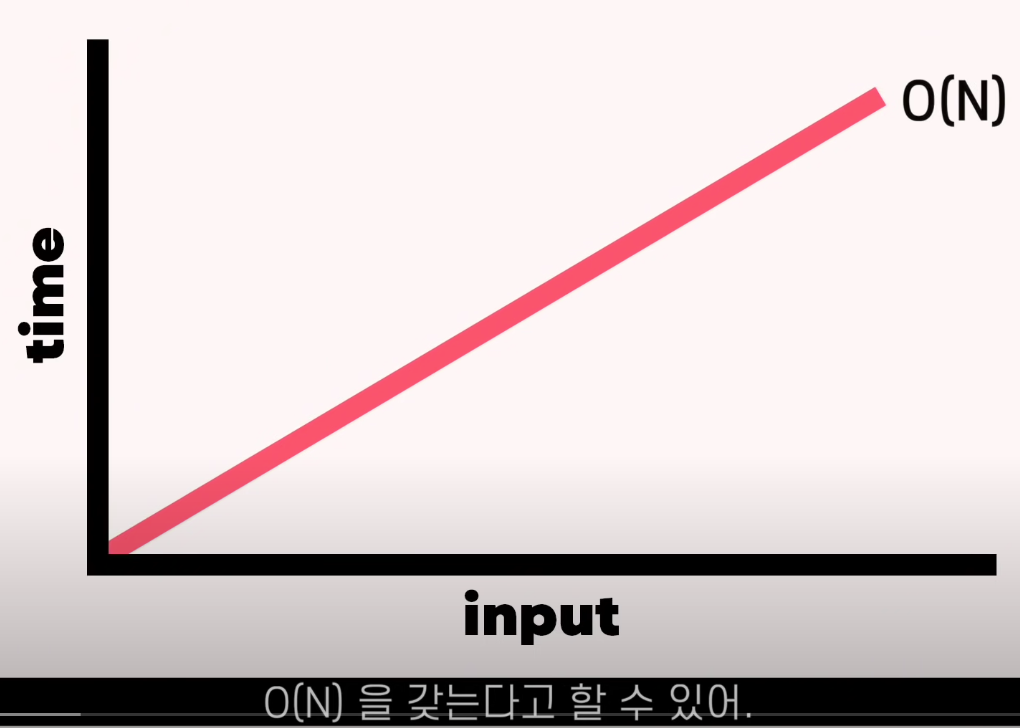
선형 검색 시간 복잡도 = O(N)
Big O 는 큰 원리에만 관심이 있어 , 인풋 사이즈가 엄청나게 커져도 관계없이 미리 정해진 숫자에 따라 작동한다.
예) 항상 200개의 스텝이 필요한 함수가 있다면 인풋 사이즈와 관계없이. 이 함수의 시간복잡도는 O(200) 이 아니라 여전히 O(1) 일것이다.
constant time(일정한 시간/상수) 이기 때문이다.
그래프로 O(1) 을 표현하면 이런모습이다.
 이런 constant(상수시간) 알고리즘의 경우 인풋 사이즈와 관계없이, 스텝이 정해진 알고리즘은 항상 선호되는 알고리즘 이지만 현실적으로 항상 그렇게 만들긴 어렵다.
이런 constant(상수시간) 알고리즘의 경우 인풋 사이즈와 관계없이, 스텝이 정해진 알고리즘은 항상 선호되는 알고리즘 이지만 현실적으로 항상 그렇게 만들긴 어렵다.
Big O 를 표현하면 다음과 같다.
O(N) 으로 불린다. 상수는 관계없기 때문이다.
예)
def print_all(arr):
for n in arr:
print(n) <- step1
for n in arr:
print(n) <- step2내가 함수를 반복한다하면
이론적으로는 이게 O(2N)이 되어야한다.
왜냐하면 각 N마다 2번 작업을 하니까
하지만 2라는 숫자는 상수이기 때문에
2는 버리고 여전히 O(N)으로 표현하게 될것이다.
왜냐하면 핵심은 바뀌지 않았기 때문이다.
O(2N) 이든 O(N) 이든 전달하려는 핵심 메세지는 동일하기 때문이다.
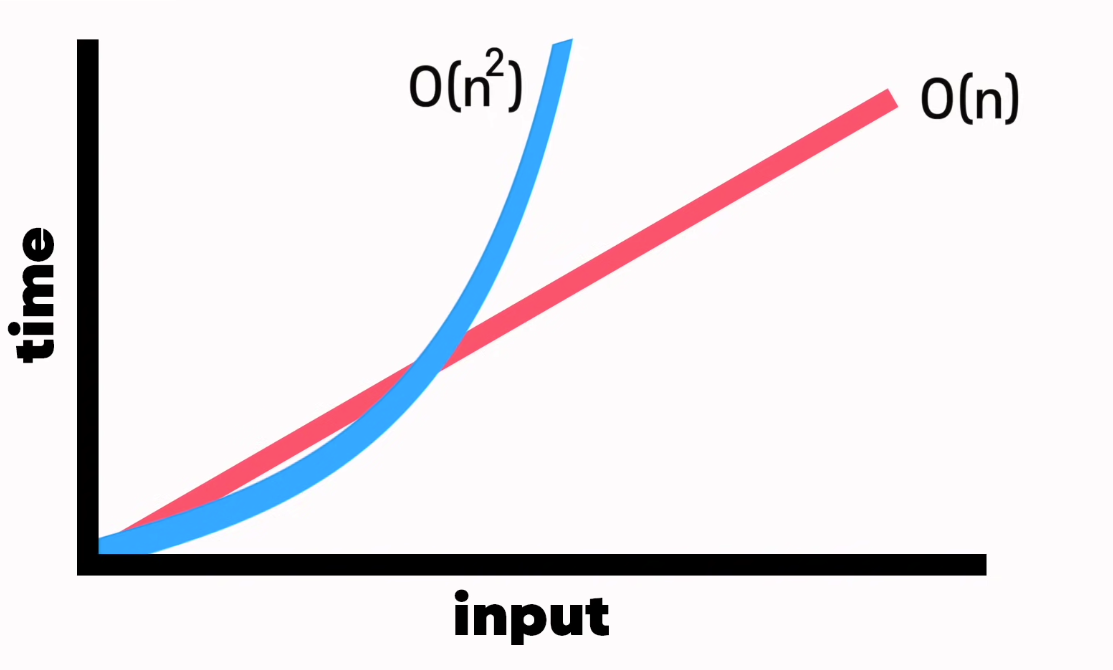
다른 시간복잡도
Quadratic Time(2차 시간) : Nested Loops(중첩반복) 이 있을때 발생한다.
def print_twice(arr):
for n in arr:
for x in arr:
print(x, n) 시간복잡도는 인풋의 N^2 이다.
인풋이 10개라면 완성하는데 100번의 스텝이 필요한것이다.
Logarithmic time (로그시간) : 이진검색 알고리즘 설명할때 쓰인다.
로그(logarithm) < - > 지수(exponent)
로그 와 지수 는 정 반대 이다.
지수
지수는 수학에서 주어진 수를 다른 수로 거듭제곱하여 표현하는 연산의 한 종류입니다. 지수는 일반적으로 밑(base)와 지수(exponent)의 두 요소로 구성됩니다.
예를 들어, "2의 3제곱"은 2를 3번 곱하는 것을 의미하며, 이를 지수로 표현하면 "2³" 또는 "2^3"으로 나타냅니다. 여기서 2가 밑이고 3이 지수입니다. 따라서 "2³"은 2를 3번 곱한 값으로 8을 의미합니다.
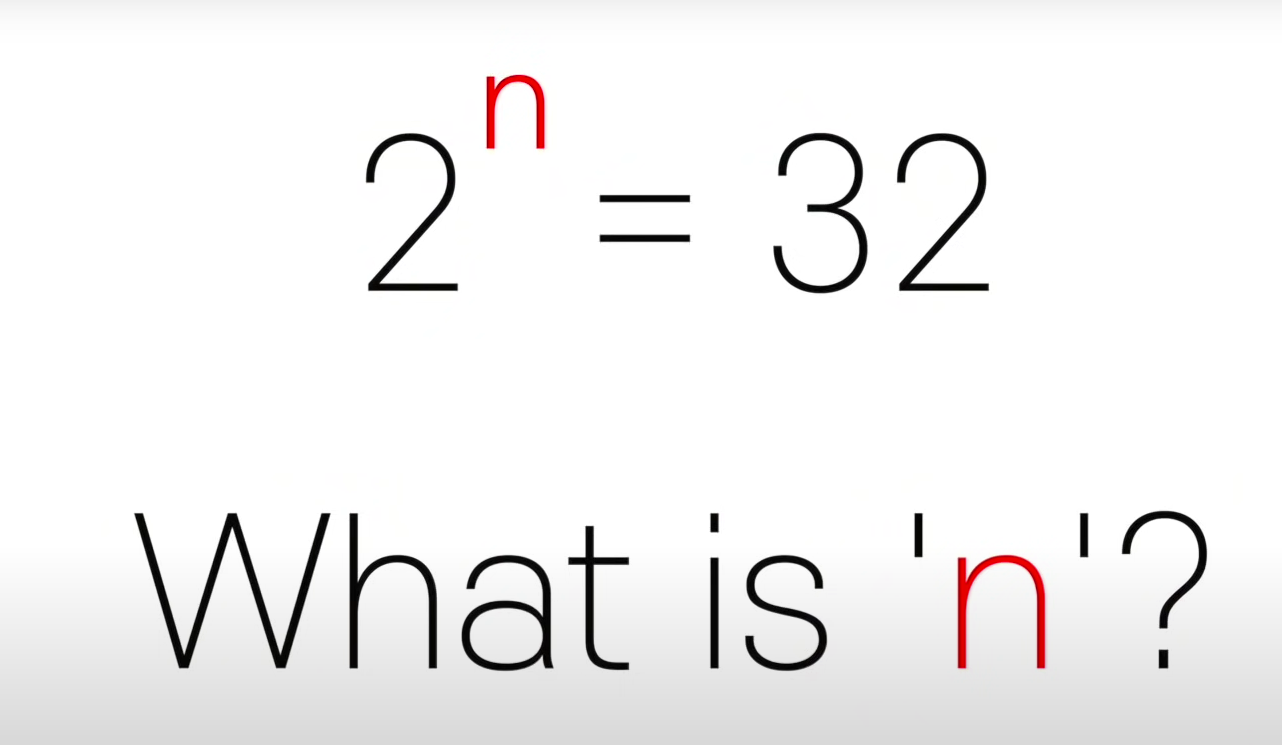
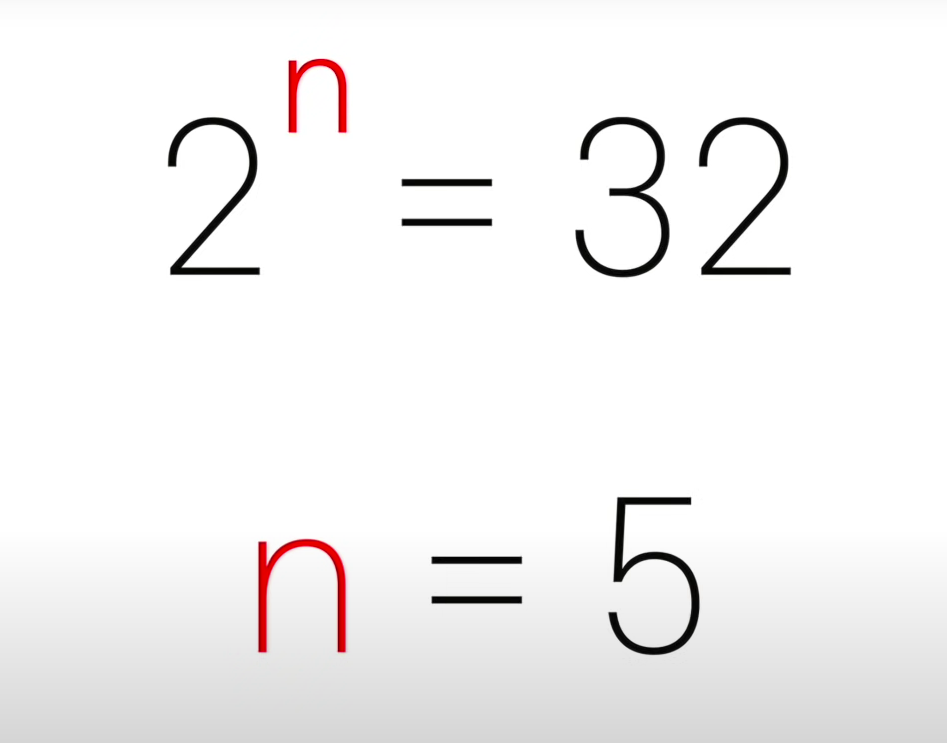
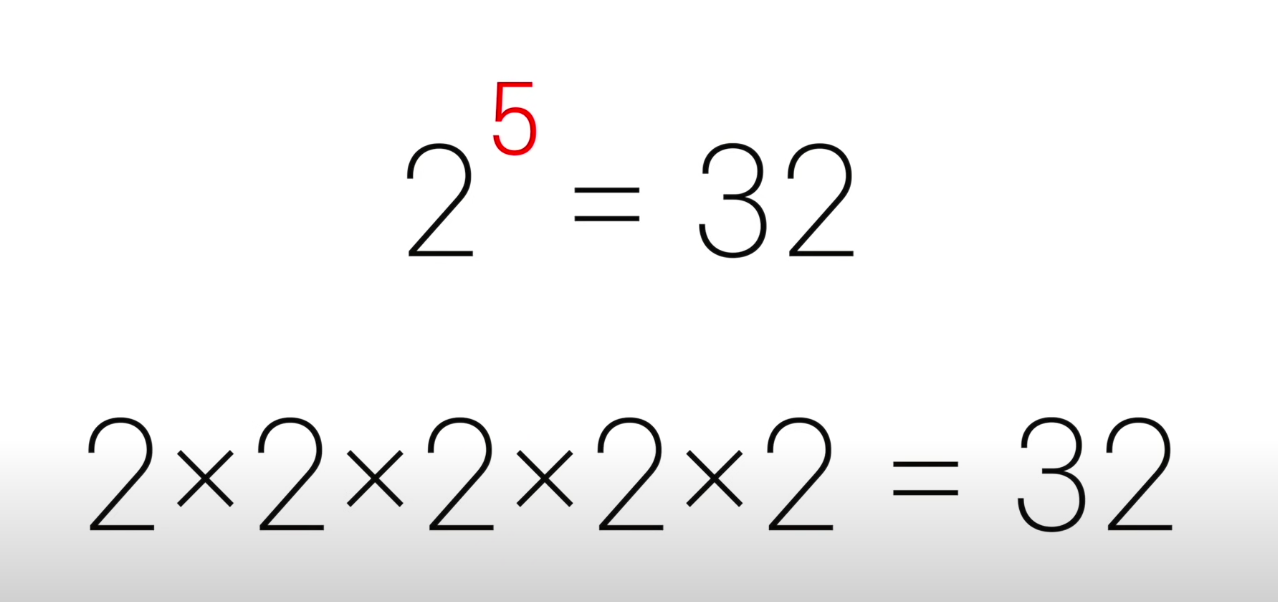 2^5 = 32가 되는것이다.
2^5 = 32가 되는것이다.
로그
로그는 수학에서 주어진 수를 다른 수로 변환하는 연산의 하나입니다. 특히 로그 함수는 지수 함수와 반대 개념으로서, 지수 함수에서 어떤 수를 밑(base)으로 거듭제곱하여 얻는 결과값을 구하는 것과 반대로, 로그 함수는 어떤 수를 어떤 밑으로 거듭제곱하여 얻는지를 구하는 연산입니다.
예를 들어, 로그 함수에서 "log₂ 8"은 밑이 2일 때, 8을 어떤 수로 거듭제곱하여 얻는지를 구하는 것이며, 정답은 3입니다. 즉, 2를 3번 거듭제곱하면 8이 됩니다.
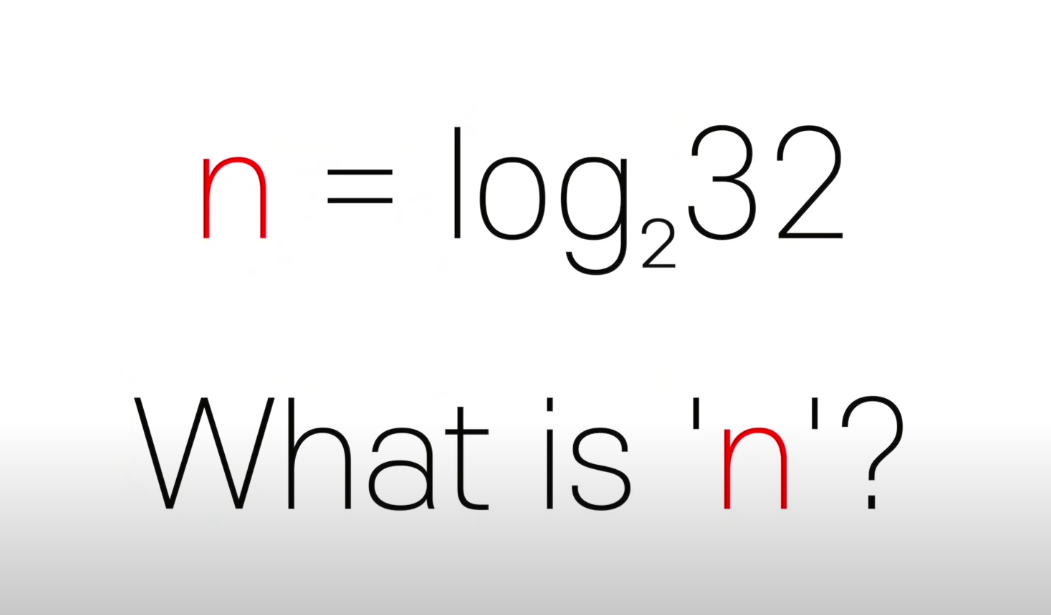 32를 2로 몇번을 나눠야 1이 나올까에 대한 질문입니다.
32를 2로 몇번을 나눠야 1이 나올까에 대한 질문입니다.
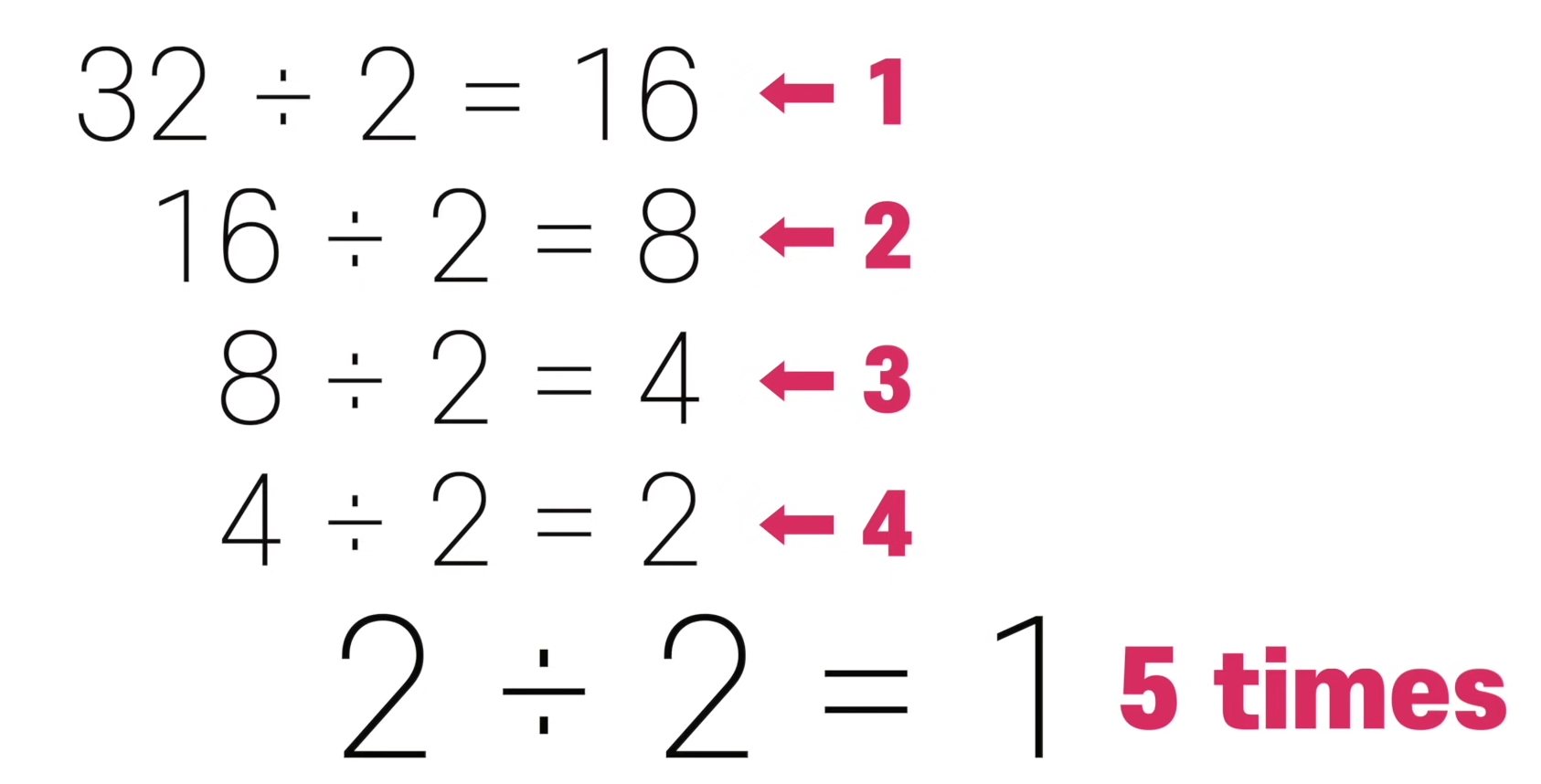
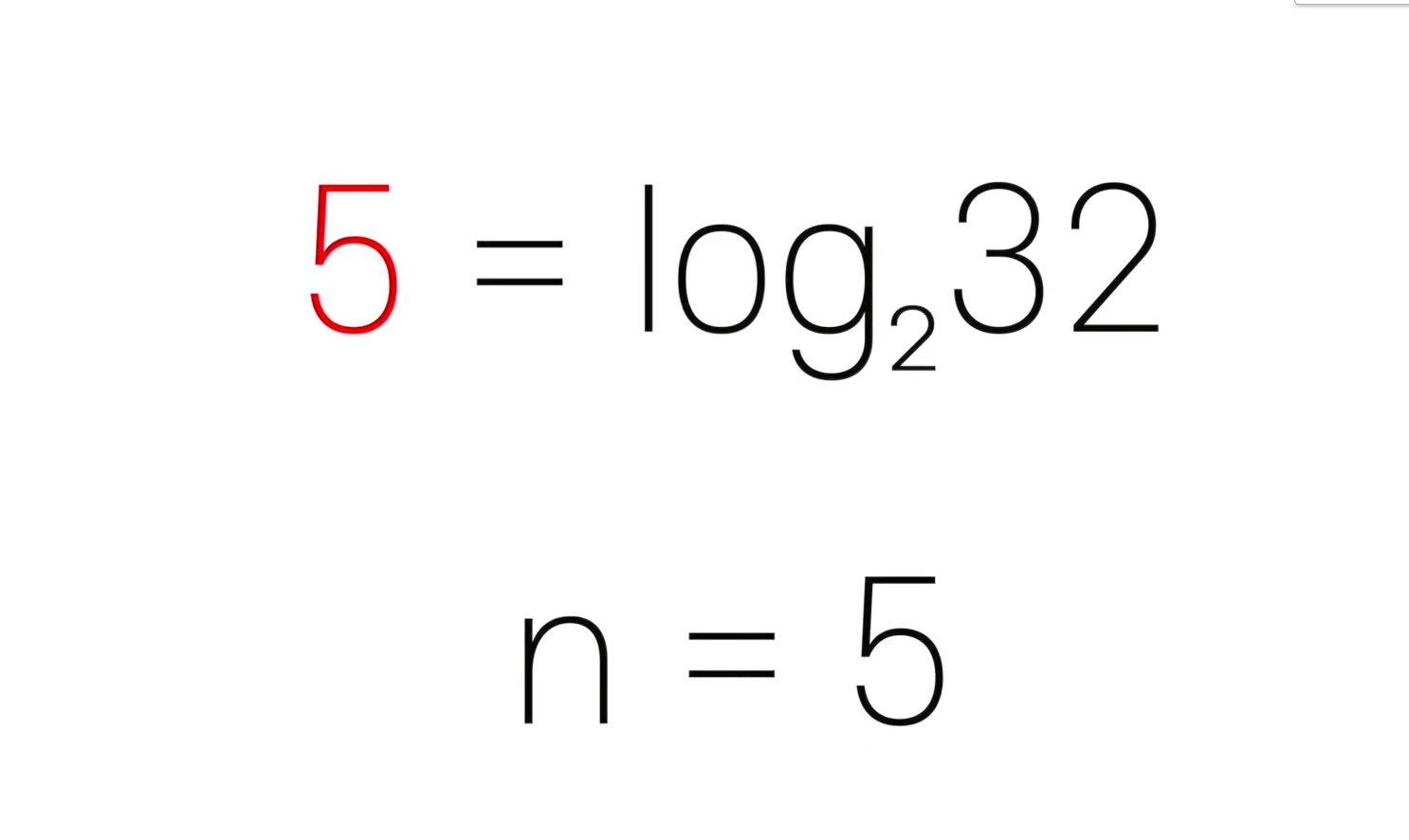
검색을 하기 위한 스텝은 +1 만 증가한다.

따라서 이진검색의 시간복잡도는 O(log n) 이다.
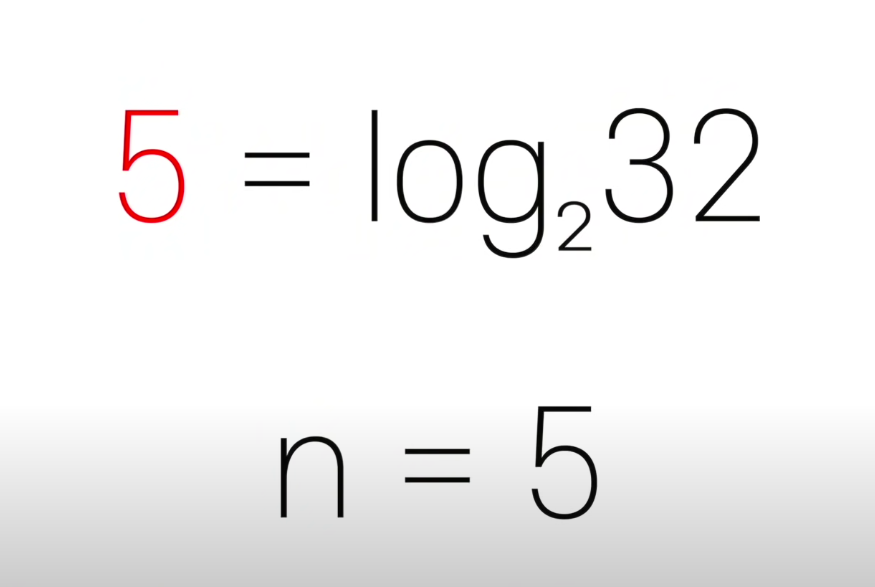
32의 밑이 2인 로그는 5인데 이 경우 BigO의 특성상 밑 숫자는 사라진다.
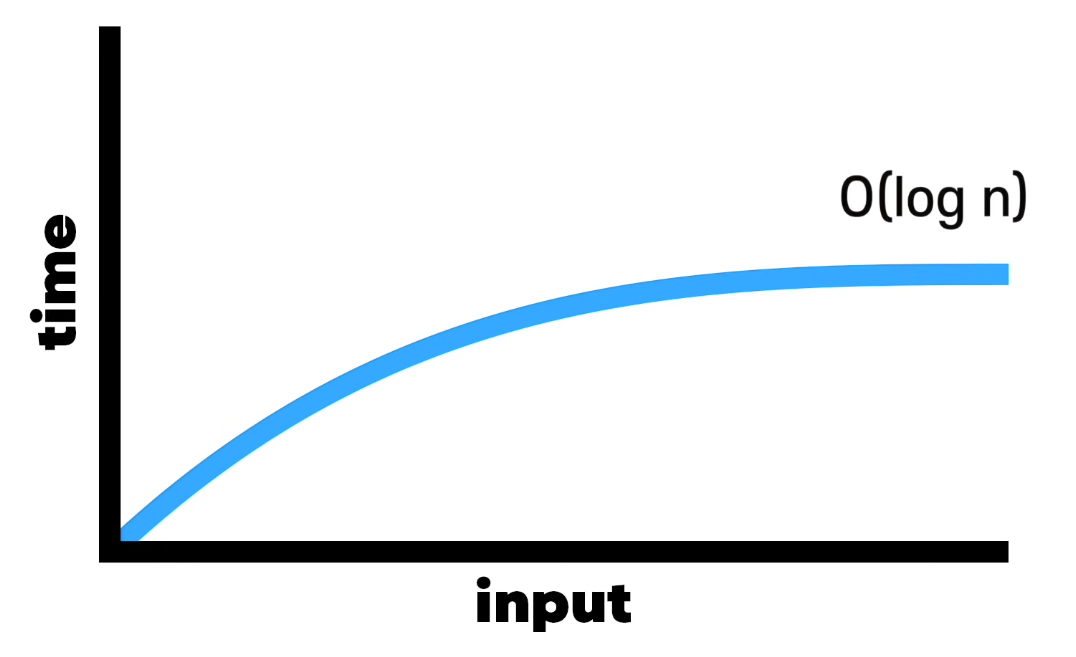
O(log n) 그래프의 모습이다.
선형시간보다는 빠르고 상수시간보다는 느리다.