11660번 문제 링크

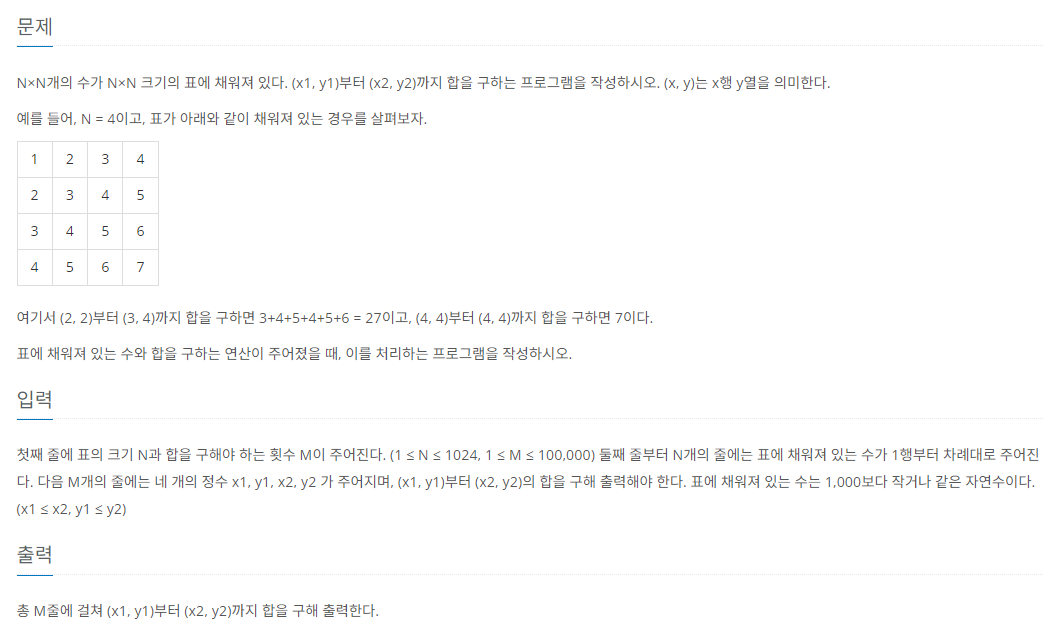
위 문제는 2차 배열의 2차원 면에서 구간합(면적)을 구하는 알고리즘 문제입니다. 이전에 수열에서 합공식을 통해 구간합을 미리 구해놓은 뒤 문제를 푸는 방식은 동일합니다.

2차 배열에서 구간합을 구하는 공식은 다음과 같습니다.

S[i][j] = S[i-1][j] + S[i][j-1] - S[i-1][j-1] + A[i][j]

위의 공식은 면적을 칠한다고 생각하면 이해하기 쉽습니다

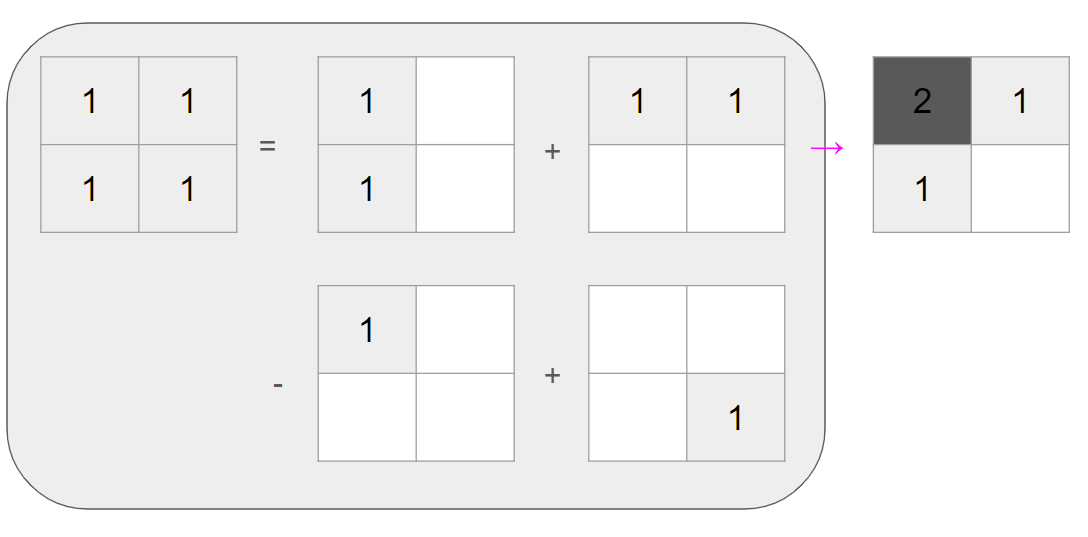
아래 그림처럼 면을 칠한다고 생각하면, 각 x열과 y열의 면들을 칠한 뒤 중복으로 칠해진 부분을 한번 지우고 구하고자 하는 위치의 면을 칠해주면 전체 면적이 칠해집니다.

위의 구간합 공식을 통해서 구간합 배열을 구한 뒤, 좌표를 통해 만들어지는 사각형의 구간합(면적)을 구해주면 문제가 해결됩니다.

x1,y1 ~ x2,y2 로 생성된 사각형의 특정된 구간합을 구하는 공식은 다음과 같습니다.

S[x2][y2] - S[x1-1][y2] - S[x2][y1-1] + S[x1-1][y1-1]

😀 성공

import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main{
    public static void main(String[] args)throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());
        
        // 일반 배열값 담기
        int[][] arr = new int[N+1][N+1];
        for(int i=1; i<=N; i++){
            st = new StringTokenizer(br.readLine());
            for(int j=1; j<=N; j++){
                arr[i][j] = Integer.parseInt(st.nextToken());
            }
        }
        
        // 요소 구간합 배열에 담기
        int[][] sum = new int[N+1][N+1];
        for(int i=1; i<=N; i++){
            for(int j=1; j<=N; j++){
                sum[i][j] = sum[i][j-1] + sum[i-1][j] - sum[i-1][j-1] + arr[i][j];
            }
        }
        
        for(int i=0; i < M; i++){
            st = new StringTokenizer(br.readLine());
            int x1 = Integer.parseInt(st.nextToken());
            int y1 = Integer.parseInt(st.nextToken());
            int x2 = Integer.parseInt(st.nextToken());
            int y2 = Integer.parseInt(st.nextToken());
            
            sb.append(sum[x2][y2] - sum[x1-1][y2] - sum[x2][y1-1] + sum[x1-1][y1-1]).append("\n");
        }
        
        br.close();
        System.out.println(sb);
    }
}

😒 실패

처음 문제를 풀었을 때에는 구간합에 대한 이해를 잘못하여 면적으로 생각 못하고 수의 긴 나열로 생각하고 잘못된 알고리즘으로 접근하여 오답이 나왔었습니다.

import java.io.IOException;
import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

public class Main{
    public static void main(String[] args)throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        StringTokenizer st = new StringTokenizer(br.readLine());
        int N = Integer.parseInt(st.nextToken());
        int M = Integer.parseInt(st.nextToken());
        
        int[][] sum = new int[N+1][N+1];
        sum[0][0] = 0;
        for(int i=1; i<=N; i++){
            sum[i][0] = 0;
            st = new StringTokenizer(br.readLine());
            for(int j=1; j<=N; j++){
                sum[0][j] = 0;
                int n = Integer.parseInt(st.nextToken());
                
                if(j == 1){
                    sum[i][j] = sum[i-1][N] + n;    
                }else{
                    sum[i][j] = sum[i][j-1] + n;
                }
            }
        }
        
        for(int i=0; i < M; i++){
            st = new StringTokenizer(br.readLine());
            int x1 = Integer.parseInt(st.nextToken());
            int y1 = Integer.parseInt(st.nextToken());
            int x2 = Integer.parseInt(st.nextToken());
            int y2 = Integer.parseInt(st.nextToken());


            if(y2 == 1){
                sb.append(sum[x2][y2] - sum[x1-1][N]).append("\n");
            }else{
                sb.append(sum[x2][y2] - sum[x1][y1-1]).append("\n");
            }
        }
        
        br.close();
        System.out.println(sb);
    }
}