1. 문제 파악

---

문제

N개의 정수로 이뤄진 수열이 있는 경우, 부분수열의 원소를 더한 값이 S가 되는 경우의 수를 구하시오.

입력

첫째 줄에 정수의 갯수 N과 S가 주어집니다.(N : 1~20, S : -1,000,000 ~ 1,000,000)
둘째 줄에 N개의 정수가 공백으로 구분되어 주어집니다.
주어진 정수의 범위는 -100,000~100,000 입니다.

출력

첫째 줄에 합이 S가 되는 부분수열의 갯수를 출력하세요.

예제

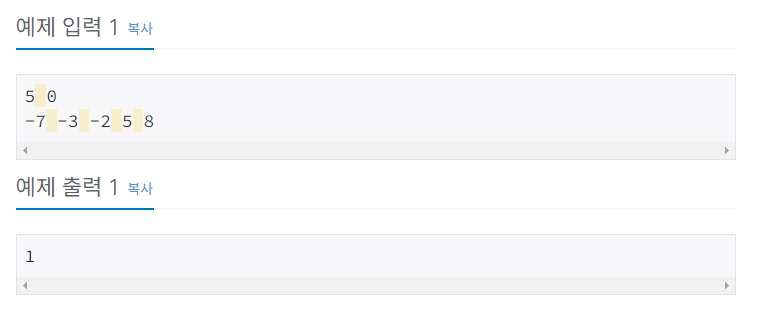
2. 접근 방법

---

해당 문제를 해석해보면, N개의 수열 내에서 일부 부분수열을 뽑아내 요소의 합을 S와 비교하여 경우의 갯수를 찾는 문제입니다.

해당 문제는 전형적인 조합 문제 입니다.

해당 문제는 수열의 일부 수열을 뽑아 다른 조합을 만들어 내는 것이 핵심 로직입니다.

이를 코드로 나타내면, 다음과 같습니다.

/**
 * 백트래킹 이용하여, 조합을 구현함.
 * r : 조합의 갯수를 의미
 * start : 조합에 사용될 정수 배열의 idx 값을 의미
 * r이 0이 되면, 조합된 수들의 합을 구해 S와 비교하여 counting
 */
import java.util.*;
import java.io.*;
public class Main {
    private static int[] arr;
    private static boolean[] visited;
    private static int n ,s, result;
    public static void main(String[] args) throws IOException {
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringTokenizer st = new StringTokenizer(br.readLine());

        n = Integer.parseInt(st.nextToken());
        s = Integer.parseInt(st.nextToken());
        st = new StringTokenizer(br.readLine());
        arr = new int[n];
        for (int i = 0; i < n; i++) {
            arr[i] = Integer.parseInt(st.nextToken());
        }

        visited = new boolean[n];
        /**
         * 5C1, 5C2, 5C3, 5C4, 5C5
         */
        for (int i = 1; i <= n; i++) {
            combination(0, i);
        }

        System.out.println(result);
    }
    // -7 -3 -2 5 8
    private static void combination(int start, int r) {
        if (r == 0) {
            int sum = 0;
            for (int i = 0; i < n; i++) {
                if (visited[i]) {
                    sum += arr[i];
                }
            }
            if (sum == s) {
                result++;
            }
            return;
        }

        for (int i = start; i < n; i++) {
            visited[i] = true;
            combination(i+1, r-1);
            visited[i] = false;
        }
    }
}