BAEKJOON 2581번: 소수

2581번 문제

참조 포스팅

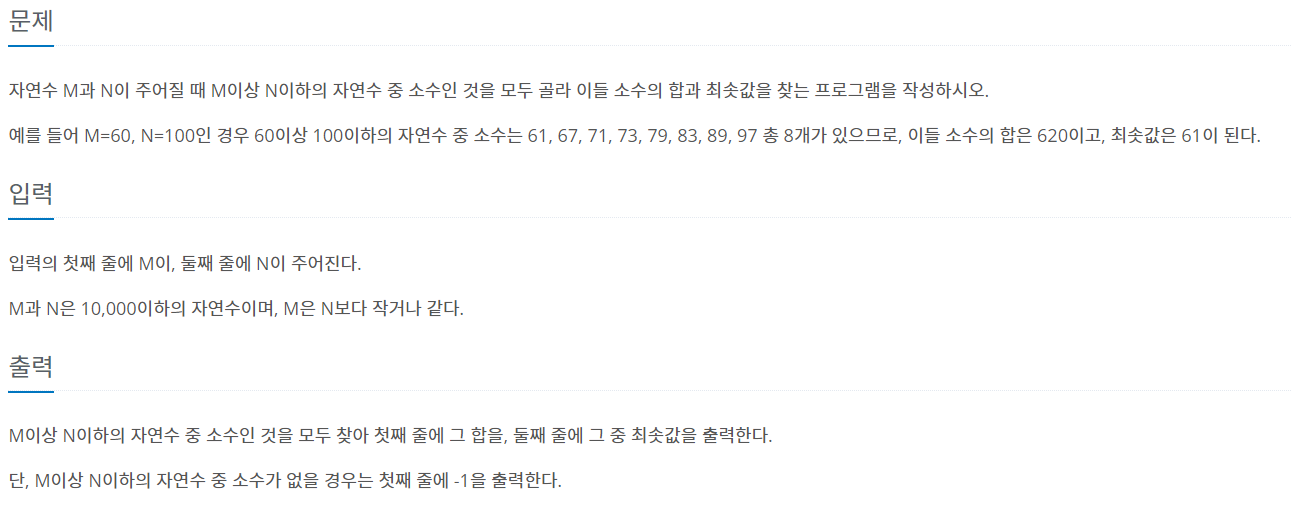
문제

🗝️포인트

• 처음 생각했던 로직
  소수는 약수가 1과 자신 오직 2개이므로, 이 점만 고려하여 로직을 짰으며, 이중 for문 사용으로 인해, 실행 시간이 320ms 정도에 출력되었다.

• 위 포스팅을 보고 느낀점
  소수를 찾기위한 최적화된 알고리즘을 학습할 수 있었으며, 이 전 코드를 최적화하여 120ms의 실행속도 까지 줄일 수 있었다.

1. 소수(Prime Number)란?

• 1보다 큰 자연수 중 1 과 그 수 자기 자신만을 약수로 갖는 자연수를 의미한다.

• 즉, 이 말은 1과 자신이 아닌 수와 모듈러(%) 연산 시 0이 나오면, 소수가 아닌 수가 된다.(1과 자신이 아닌 수가 약수로 존재하게 되므로)

2. 에라토스테네스의 체

• 소수를 구하는 대표적인 방법 중 하나

• 어떤 N이 두 개이상 곱셈(인수)으로 나타낼 수 있을 때, 인수 중 한 개 이상은 반드시 √N보다 작거나 같다.

• 즉, √N의 배수는 합성수를 의미한다.

  따라서 k=2 부터 √N 이하까지 반복하여 자연수들 중 k를 제외한 k의 배수들을 제외시킨다"

• 위 공식에 제외된 수가 아닌 수들이 소수이다.

boolean[] prime = new boolean[]; // 소수 판별용 배열

// 제곱근 함수 : Math.sqrt()
for(int i = 2; i <= Math.sqrt(N); i++) {
        
	// 이미 체크된 배열은 건너뛰기
	if(prime[i] == true) {
		continue;
	}
        
	// i 의 배수들을 걸러주기 위한 반복문
	for(int j = i * i; j < prime.length; j = j+i) {
		prime[j] = true;
	}
}

제출 코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.io.IOException;
 
public class Main {
 
	public static boolean prime[];
	
	public static void main(String[] args) throws IOException {
 
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		
		int M = Integer.parseInt(br.readLine());
		int N = Integer.parseInt(br.readLine());
		
		prime = new boolean[N + 1];	

		get_prime();
	
		int sum = 0;
		int min = Integer.MAX_VALUE;
		for(int i = M; i <= N; i++) {
			if(prime[i] == false) {
				sum += i;
				if(min == Integer.MAX_VALUE) { 
					min = i;
				}
			}
		}
		
		if(sum == 0) {
			System.out.println(-1);
		}
		else {
			System.out.println(sum);
			System.out.println(min);
		}
		
	}
 
	public static void get_prime() {
		prime[0] = true;
		prime[1] = true;
		
		for(int i = 2; i <= Math.sqrt(prime.length); i++) {
			if(prime[i]) continue;
			for(int j = i * i; j < prime.length; j += i) {
				prime[j] = true;
			}
		}
		
	}
}