2750번 문제 링크

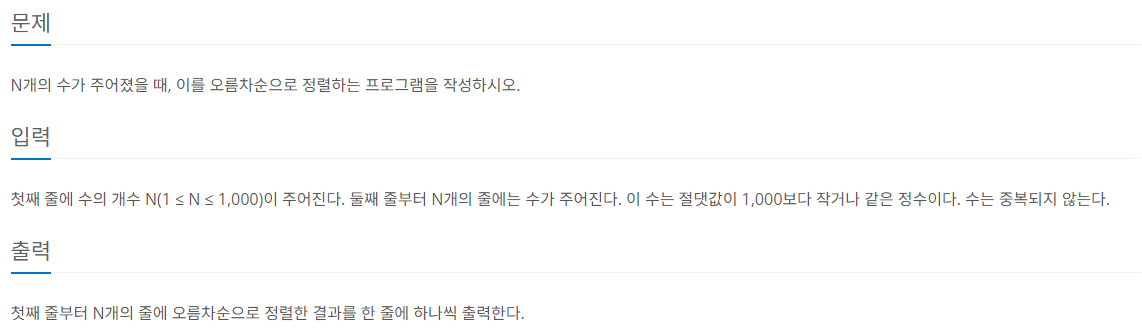
위 문제는 N의 최대 범위가 1,000으로 매우 작기 때문에 O(n^2) 시간 복잡도 알고리즘으로 풀 수 있다. 버블 정렬의 시간 복잡도가 O(n^2)이기 때문에 버블 정렬 알고리즘을 이용해 정렬해도 시간 복잡도 안에서 해결이 가능하다.

버블 정렬 알고리즘의 과정은 다음과 같다.
1. 비교 연산이 필요한 루프 범위를 설정.
2. 인접한 두 데이터를 비교.
3. swap 조건(오름차순)에 부합하면 연산을 수행.
4. 루프 범위까지 2~3 과정을 반복.
5. 정렬할 영역을 지정하는데, 이전에 수행했던 정렬 영역은 제외한다.(오름차순이기 때문에 마지막 인덱스 제외)
6. 비교 대상이 없을때까지 1~5번을 반복.

• 핵심은 swap이 한번도 발생하지 않은 경우에, 모든 영역이 정렬되었음을 의미한다.

😀 성공

import java.io.*;

public class Main{
    static int[] arr; // 정렬 대상을 담은 배열
    static int change; // 정렬 발생 횟수
    public static void main(String[] args)throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        int N = Integer.parseInt(br.readLine());
        
        // 입력 초기화
        arr = new int[N];
        for(int i=0; i < N; i++){
            arr[i] = Integer.parseInt(br.readLine());
        }
        
        // 연산
        while(true){
            change = 0;// 정렬 횟수 초기화
            for(int i=0; i < N-1; i++){
                swap(i); // 오름차순 정렬 메서드
            }
            if(change == 0)  // 정렬 횟수가 없는 경우, 모두 정렬되었다고 판단하여 버블 정렬 종료
                break;
            else 
                N--; // 정렬이 수행된 항목 제외
        }
        
        // 출력
        for(int i=0; i < arr.length; i++){
            sb.append(arr[i]).append("\n");
        }
        
        br.close();
        System.out.println(sb);
    }
    
    static void swap(int i){
        if(arr[i] > arr[i+1]){
            int tmp = arr[i];
            arr[i] = arr[i+1];
            arr[i+1] = tmp;
            change++;
        }
    }
}

👍 재시도

import java.io.*;

public class Main{
    static int[] arr;
    static int change;
    public static void main(String[] args)throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        StringBuilder sb = new StringBuilder();
        int N = Integer.parseInt(br.readLine());
        
        // 입력
        arr = new int[N];
        for(int i=0; i < N; i++){
            arr[i] = Integer.parseInt(br.readLine());
        }
        
        // 버블 정렬
        bubbleSort(N-1);
        
        // 출력
        for(int i=0; i < arr.length; i++){
            sb.append(arr[i]).append("\n");
        }
        br.close();
        System.out.println(sb);
    }
    
    static void bubbleSort(int N){
        change = 0;
        
        for(int i = 0; i < N; i++){
            swap(i);
        }
        
        if(change == 0) {
            return;
        }
        else{
            N--;
            bubbleSort(N);
        }
    }
    
    static void swap(int i){
        if(arr[i] > arr[i+1]){
            int tmp = arr[i];
            arr[i] = arr[i+1];
            arr[i+1] = tmp;
            change++;
        }
    }
}

2024.02.07 정렬 문제를 복습하던 중 해당 제출 코드를 재귀호출 형태로 바꿔봐도 되겠다는 생각으로 bubbleSort 라는 메서드를 밖에 정의하여 메인 메서드에서 호출하도록 하는 방식으로 구현하였습니다.

또한, 기존의 while 문 대신 재귀 호출을 통해 change == 0 조건을 충족하기 전까지 재귀호출하도록 구현하여 성능을 4ms 정도 개선하였습니다