구간합의 핵심이론

구간 합 알고리즘 활용을 위해서는 합 배열을 구하는 것이 선행되어야 합니다. 배열 A가 있을 때, 합 배열 S는 다음과 같이 정의합니다.

1차 배열

---

> 합배열 정의 - S[i] = A[0] + A[1] + A[2] + ... + A[n-1] + A[n]

위처럼 합배열을 미리 구해놓으면 기존 배열의 일정 범위의 합을 구하는 시간 복잡도가 O(N)에서 O(1)로 감소하게 됩니다.

합배열을 구하는 공식은 아래와 같습니다.

S[i] = S[i-1] + A[i]

위처럼 구현된 합 배열을 이용하면 구간 합 역시 쉽게 구할 수 있습니다. i에서 j까지 구간합은 다음과 같습니다.

S[j] - S[i-1]

2차 배열

---

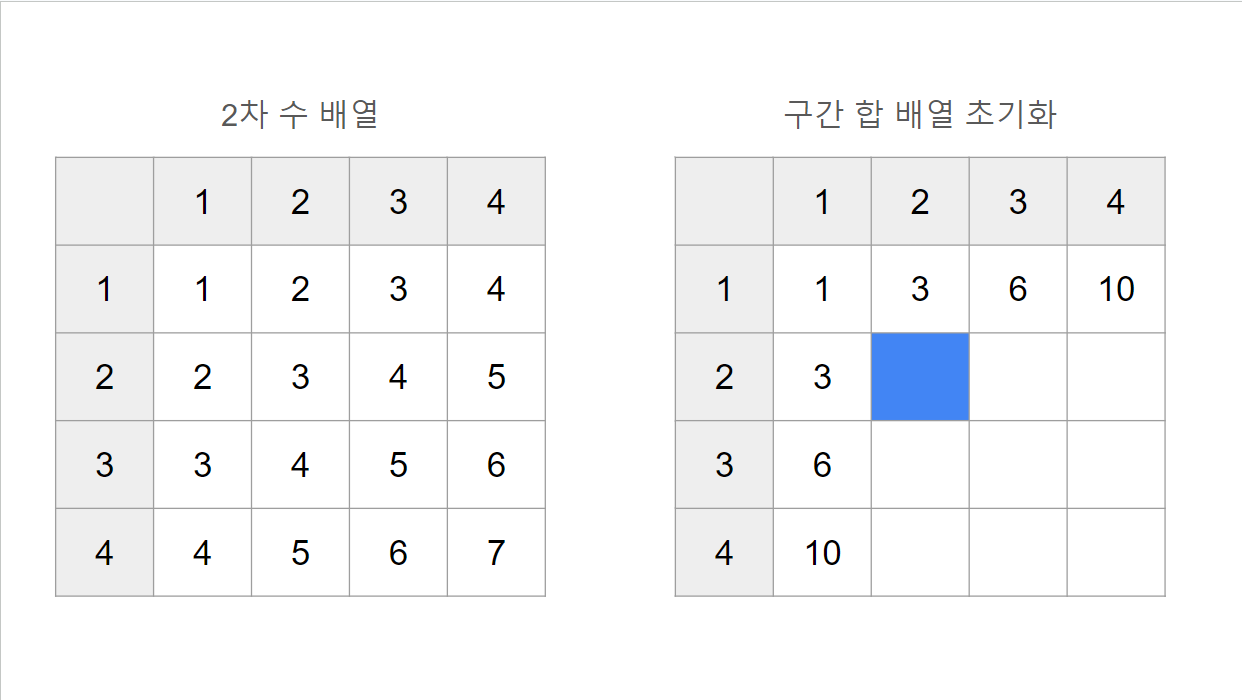
위 그림에서 보듯이 배열의 2행 2열의 값을 구하기 위해서는 어떻게 해야 할까요?

• 구하려는 위치를 x = i, y = j 라고 하면 다음과 같습니다.

구간합 정의

위의 공식은 두 구간합에서 중복되어 더해진 i-1, j-1 구간합을 한번 빼 준 뒤 현재 배열의 요소 값을 더해주는 식으로 구해주면 된다. 땅따먹기로 생각하면 이해가 조금 더 쉬울 수도 있다.

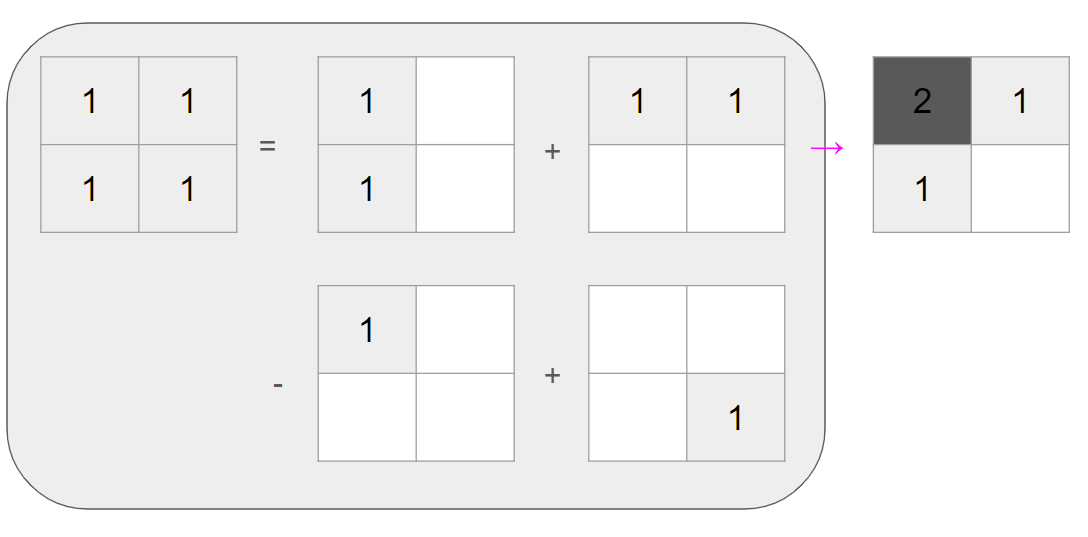
2차 배열에서 구간 합을 구하기 위해서는 좌표 영역에 모든 영역이 칠해진 상태이어야 합니다. 위에서 처럼 (1,2) 구간합과 (2,1) 구간합을 더해준 뒤 중복되는 (1,1) 구간합을 빼줍니다. 이 후에 구하고자 하는 구간합 위치의 요소를 더해주면 구간합이 나옵니다.

시작점 또한 변수인 구간합을 구하기

예를 들어 (2,2) ~ (3,4) 위치의 구간합을 구해야 하는 경우에 다음 공식을 적용하면 됩니다. 다음과 같이 그림으로 설명하겠습니다.

전체 구간합에서 행과 열이 1씩 작은 구간합을 빼준 뒤 중복으로 뺐던 부분을 더해주면, 원하는 시작점에서 끝점까지의 구간합을 구할 수 있습니다.💪

출처

• Doit 알고리즘 코딩테스트 - 자바편