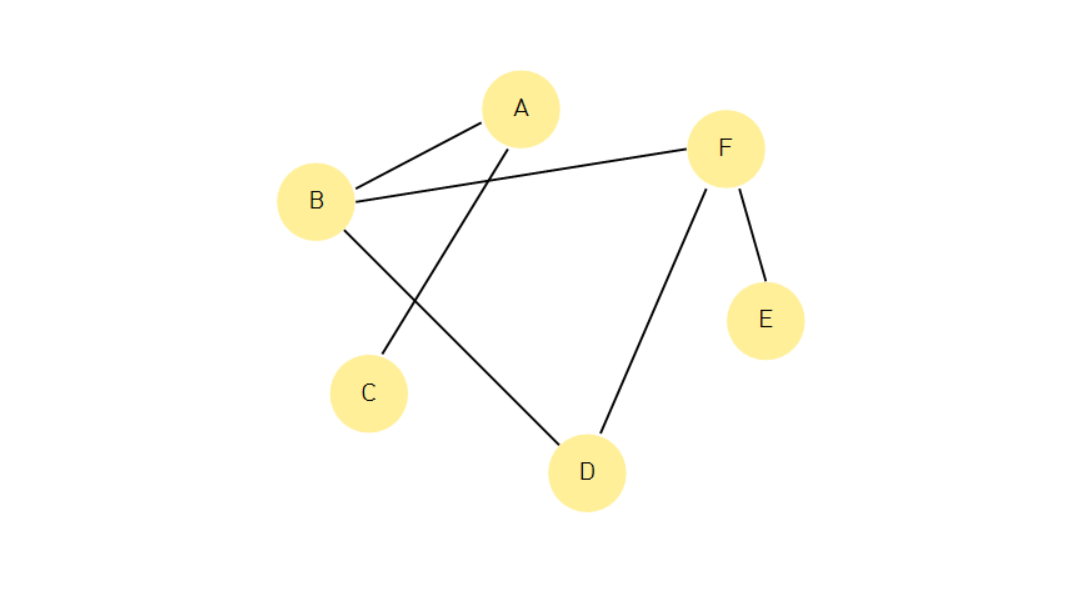
그래프 용어
-
노드
그래프에서 하나의 데이터 단위를 나타내는 객체 -
엣지
그래프에서 두 노드의 직접적인 연결 관계 데이터
- 방향 그래프(directed graph): 엣지들이 방향을 갖는 그래프
- 가중치 그래프(weighted graph): 엣지들이 어떤 정보를 나타내는 수치를 가진 그래프
-
차수
하나의 노드에 연결된 엣지들의 수
방향 그래프에서는 노드를 떠나는 엣지의 수를 출력 차수, 들어오는 엣지의 수를 입력 차루라 한다. -
경로
한 노드에서 나른 노드까지 가는 길
- 비가중치 그래프: 한 경로에 있는 엣지의 수가 경로의 거리
- 가중치 그래프: 한 경로에 있는 엣지의 가중치의 합이 경로의 거리
최단 경로: 두 노드 사이의 경로 중 거리가 가장 짧은 경로
사이클: 한 노드에서 시작해서 다른 노드로 돌아오는 경로
BFS(Breadth First Search)
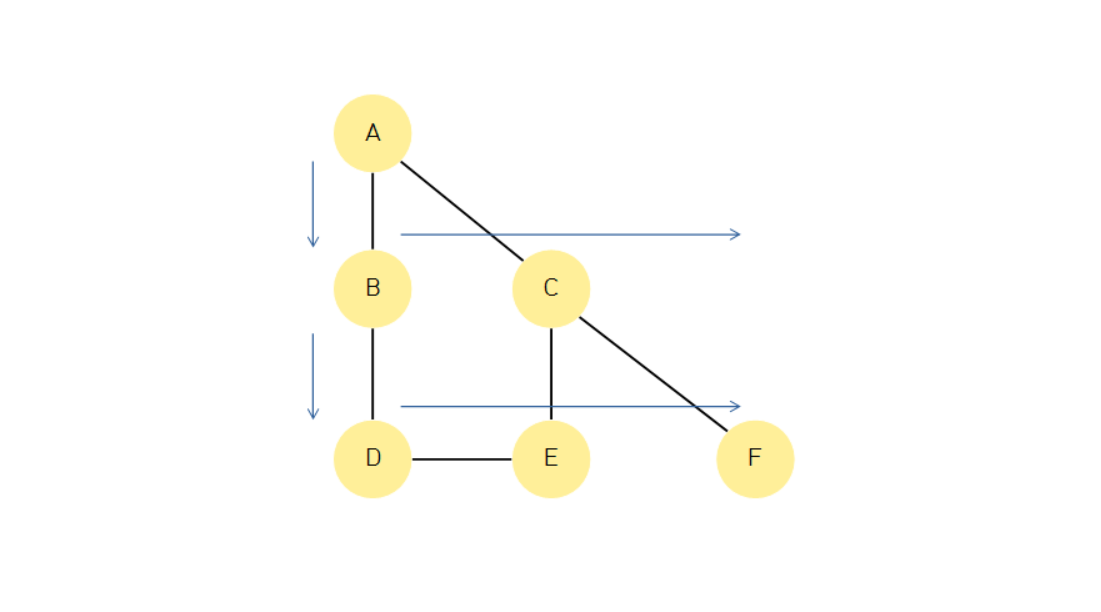
그래프를 너비 우선적으로 탐색
큐를 사용
방문했다는 boolean 타입의 데이터 사용
비가중치 그래프에서 최단 경우 알고리즘으로 사용
BFS 알고리즘
시작 노드를 방문 표시 후, 큐에 넣는다.
큐에 아무 노드가 없을 때까지 반복:
큐 가장 앞 노드를 꺼낸다.
꺼낸 노드에 인접한 노드들을 모두 탐색:
처음 방문한 노드일 경우:
방문한 노드 표시를 해준다.
큐에 넣어준다.DFS(Depth First Search)
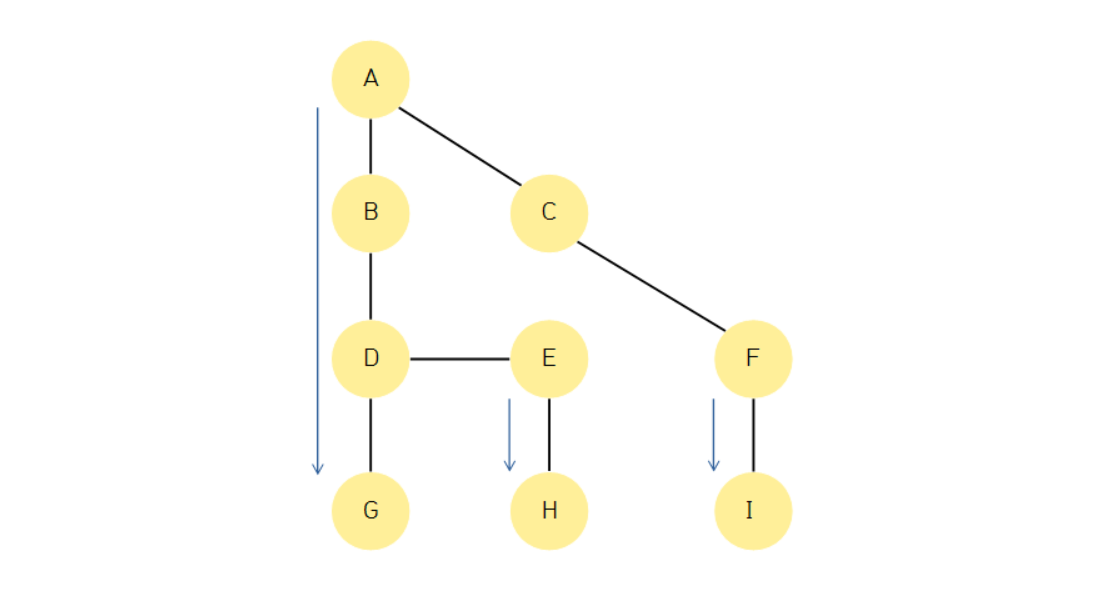
그래프를 깊이 우선적으로 탐색
스택 사용
스택에 넣었다는 확인과 방문을 끝냈다는 boolean 타입의 데이터 2개 사용
DFS 알고리즘
방문: done, 스택: check
시작 노드를 check 표시 후, 스택에 넣는다.
스택에 아무 노드가 없을 때까지 반복:
스택 가장 위 노드를 꺼낸다.
노드를 done 표시한다.
인접한 노드를 모두 탐색:
처음 방문하거나 스택에 없는 노드일 경우:
check 표시를 해준다.
스택에 넣는다.최단 경로 알고리즘
최단 경로용 BFS - 비가중치 그래프
기존 BFS에서 노드에 이전 노드를 저장하는 predecessor 데이터를 저장
predecessor를 사용한 백트래킹(도착점에서 시작점으로 거꾸로 찾아가는 방법)으로 시작노드로부터 원하는 노드까지의 최단 경로를 구할 수 있다.
시작 노드를 방문 표시 후, 큐에 넣는다.
큐에 아무 노드가 없을 때까지 반복:
큐 가장 앞 노드를 꺼낸다.
꺼낸 노드에 인접한 노드들을 모두 탐색:
처음 방문한 노드일 경우:
방문한 노드 표시를 해준다.
predecessor 변수를 큐에서 꺼낸 노드로 설정
큐에 넣어준다.Dijkstra - 가중치 그래프
노드에 distance, predecessor, complete 데이터를 저장
distance: 특정 노드까지의 최단 거리 예상치, 현재까지 아는 정보로 계산한 최단 거리, 초기값: 무한대(python: inf)
predecessor: 현재까지 최단 경로에서 바로 직전의 노드, 초기값: None
complete: 특정 노드를 완전히 파악했는지 표시하기 위한 변수, 초기값: False
시작점의 diatance를 0, predecessor를 None으로 설정
모든 노드가 complete 일 때까지 반복:
complete하지 않은 노드 중 distance가 가장 작은 노드를 선택
이 노드에 인접한 노드 중 complete하지 않은 노드를 탐색:
각 엣지를 relax
현재 노드를 complete 처리Relaxation
A에서 B를 방문하면서 B의 distance, predecessor를 바꾸는 것
ex) 엣지(A,B)를 relax한다.
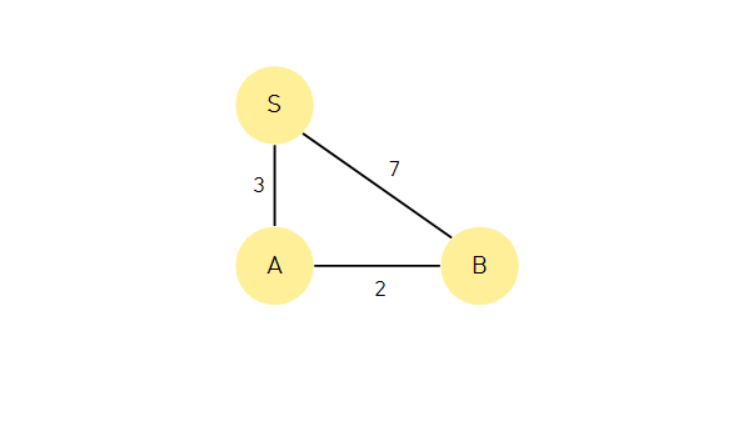
A.distance + 엣지(A,B) 가중치 < B.distance 일 경우
| 기존 B | Relaxation B | |
|---|---|---|
| distance | 7 | 5 |
| predecessor | start_node | A |
