트리
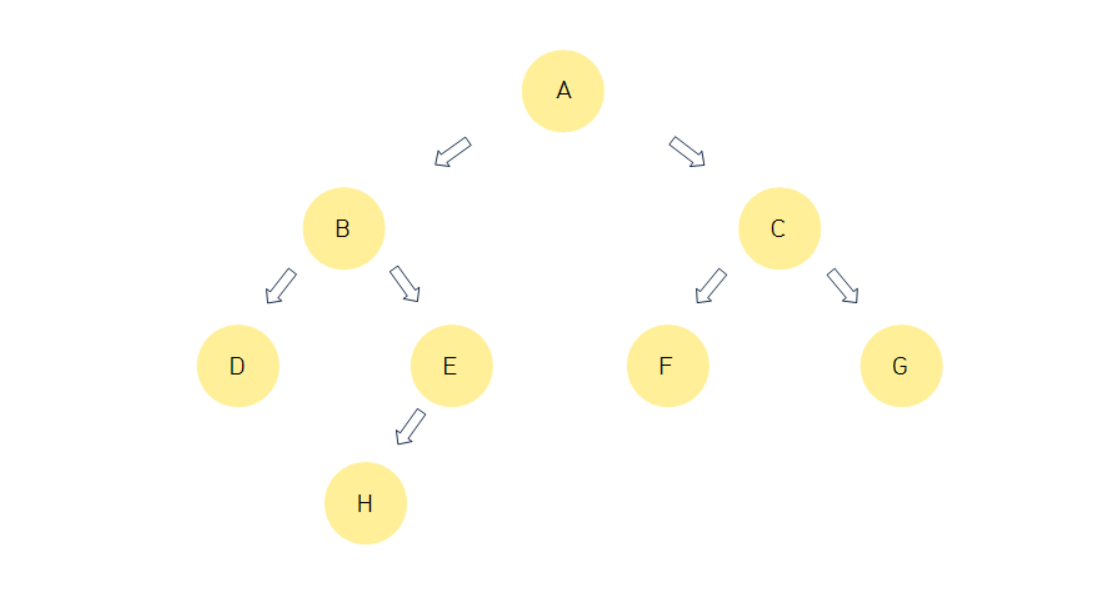
계층적 구조를 가진 자료 구조
용어
root 노드(뿌리 노드): A / 트리의 시작 노드
부모 노드: 특정 노드의 직속 상위 노드, C,F,G 그룹에서 C는 F,G의 부모 노드
자식 노드: 특정 노드의 직속 하위 노드, C,F,G 그룹에서 F,G는 C의 자식 노드
형제 노드: 같은 부모를 갖는 노드, D, E는 부모가 B이기 때문에 D, E는 형제 노드
leaf 노드(말단 노드): 자식 노드를 갖지 않은 가장 말단에 있는 노드
깊이: 특정 노드가 root 노드에서 떨어져 있는 거리, 해당 노드로 가기 위해서 root 노드에서 몇 번 아래로 내려와야 하는지를 나타낸다.
레벨: 깊이+1
높이: 트리에서 가장 깊이 있는 노드의 깊이
- 트리의 활용
계층적 관계가 있는 데이터를 컴퓨터에서 사용할 수 있다.
컴퓨터 과학의 다양한 문제를 기발하게 해결할 수 있다.
흔히 사용하는 여러 추상 자료형을 구현할 수 있다.
트리의 종류
정 이진 트리(Full Binary Tree)
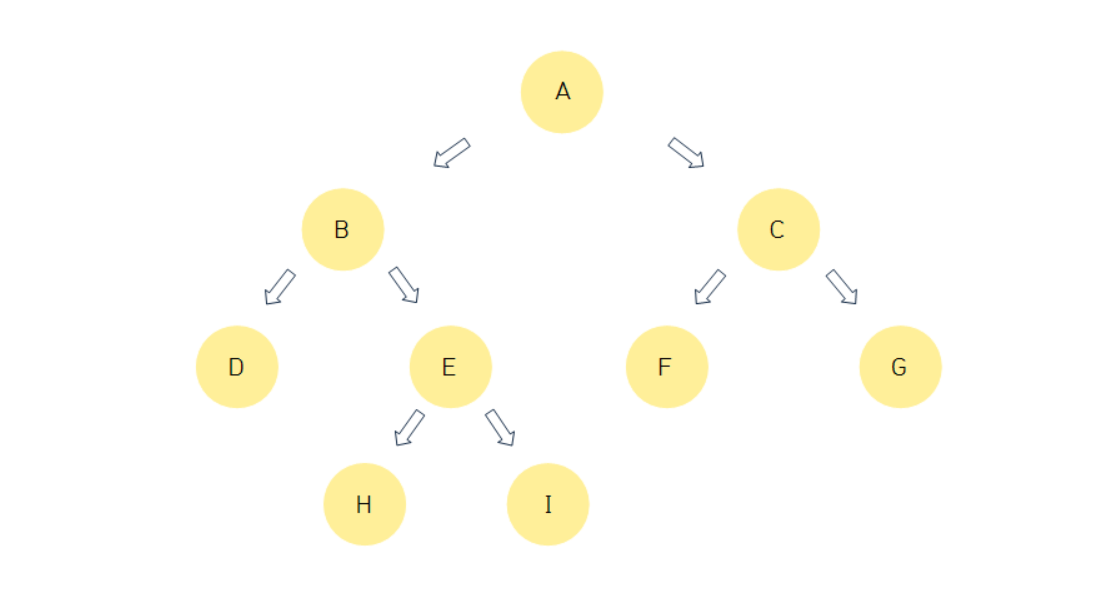
모든 노드가 2개 또는 0개의 자식을 갖는 이진 트리
완전 이진 트리(Complete Binary Tree)
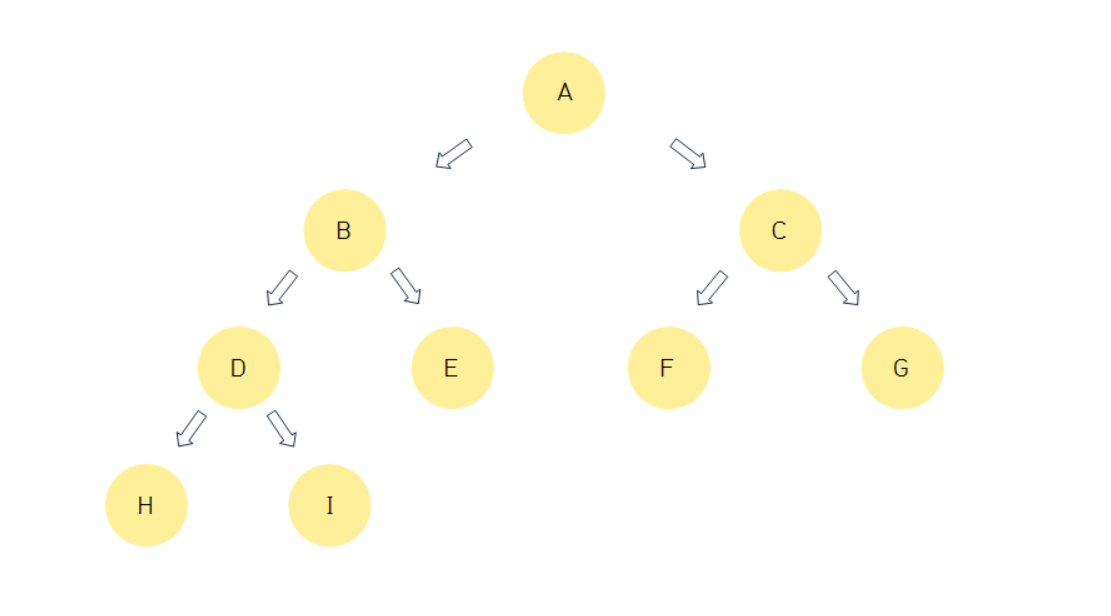
이진 트리 중에서도 마지막 레벨 직전의 레벨 까지는 모든 노드들이 다 채워진 트리
마지막 레벨에서는 노드들이 왼쪽부터 오른쪽 방향으로 노드들이 채워진다.
노드가 n개라고 할 때, 높이는 항상 lg(n)에 비례
포화 이진 트리(Perfect Binary Tree)
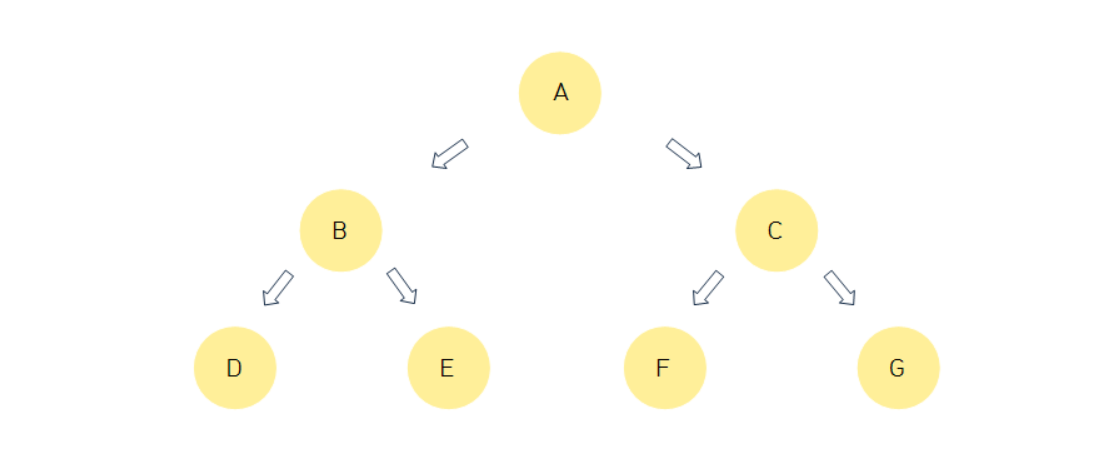
모든 레벨이 빠짐없이 노드로 채워져있는 이진 트리
정 이진 트리와 완전 이진 트리의 특성을 모드 갖는다.
트리 순회

자료 구조에 저장된 모든 데이터를 도는 것
재귀 함수를 사용
pre-order
재귀를 하기 전에 현재 노드 데이터를 출력
- 현재 노드 데이터를 출력한다.
- 재귀적으로 왼쪽 부분 트리 순회
- 재귀적으로 오른쪽 부분 트리 순회
출력: A-B-D-E-H-I-C-F-G
post-order
재귀를 한 이후 현재 노드 데이터를 출력
- 재귀적으로 왼쪽 부분 트리 순회
- 재귀적으로 오른쪽 부분 트리 순회
- 현재 노드 데이터를 출력한다.
출력: D-H-I-E-B-F-G-C-A
in-order
- 재귀적으로 왼쪽 부분 트리 순회
- 현재 노드 데이터를 출력한다.
- 재귀적으로 오른쪽 부분 트리 순회
출력: D-B-H-E-I-A-F-C-G
힙
속성
힙은 완전 이진 트리
모든 노드의 데이터는 자식 노드들의 데이터보다 크거나 같다.
활용 방법
1. 정렬
2. 우선순위 큐 구현
힙 정렬
배열, 리스트를 사용하여 구현
- 완전 이진 트리를 힙이 되도록 만든다.(최대 힙)
- root와 마지막 노드를 바꾼다.
- 바꾼 노드(마지막 노드 - 배열, 리스트의 마지막 인덱스)는 없는 노드 취급한다.
- 새로운 노드가 힙 속성을 지킬 수 있도록 힙을 만든다.
- 2~4의 과정을 모든 인덱스를 돌 때 까지 반복한다.
내림 차순으로 정렬하고 싶다면 힙 속성을 반대로 하여 구현이 가능하다.
다른 정렬 알고리즘과 비교
| 정렬 알고리즘 | 시간 복잡도 |
|---|---|
| 선택 정렬 | O(n^2) |
| 삽입 정렬 | O(n^2) |
| 합병 정렬 | O(nlg(n)) |
| 퀵 정렬 | 평균: O(nlg(n)), 최악: O(n^2) |
| 힙 정렬 | O(nlg(n)) |
우선순위 큐
데이터를 저장할 수 있다.
저장한 데이터가 우선순위 순서대로 나온다.
힙에 데이터 삽입하기
- 힙의 마지막 인덱스에 데이터 삽입
- 삽입한 데이터와 부모 노드의 데이터를 비교하여 부모 노드가 더 작다면 위치 교환
- 트리가 힙이 될 때까지 2를 반복
힙에서 데이터 제거하기
우선순위가 높은 데이터를 root로 하여 root를 제거
- 루트 노드를 제거
- 루트 자리에 가장 마지막 노드를 삽입
- 망가진 힙 속성을 복원
우선순위 큐 평가
| 구조 | 데이터 삽입 | 데이터 추출 |
|---|---|---|
| 배열 | O(1) | O(n) |
| 연결 리스트 | O(1) | O(n) |
| 정렬된 배열 | O(n) | O(1) |
| 정렬된 연결 리스트 | O(n) | O(1) |
| 힙 | O(lg(n)) | O(lg(n)) |
기존에 동적 배열과 더블리 링크드 리스트가 정렬이 된 상태라고 가정하면
새로운 데이터를 삽입할 경우가 많다면 힙으로 구현하는 것이 효율적이고 데이터를 추출할 경우가 많다면 동적 배열, 더블리 링크르 리스트로 구현하는 것이 효율적이다.
