DFS/BFS
알고리즘 문제를 풀다보면 완전탐색 문제가 많이 나온다 그래서 탐색의 가장 기본이 되는 DFS, BFS에 대해서 간단하게 정리를 해보려고 한다.
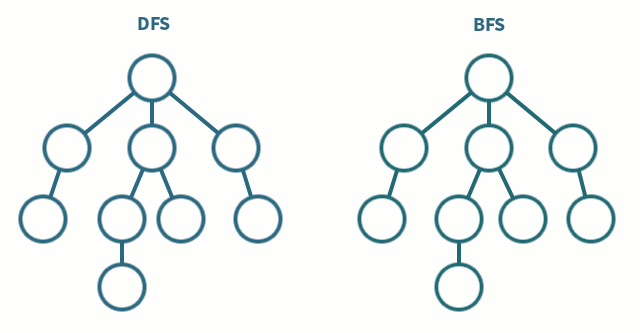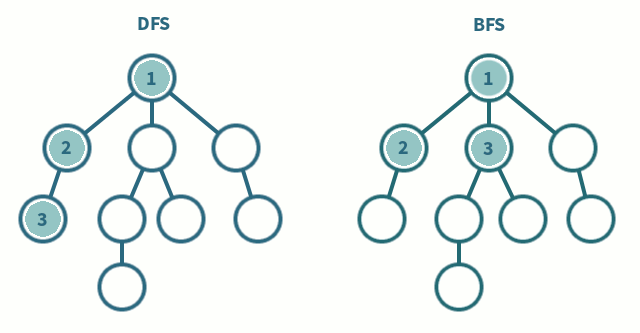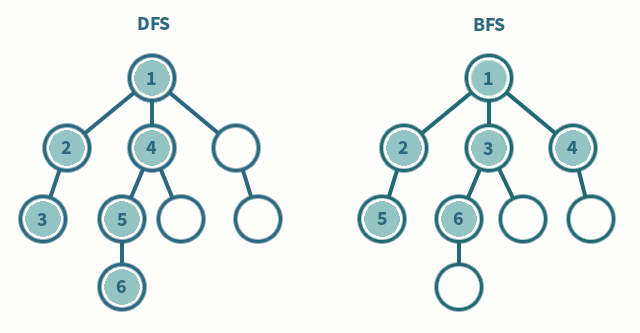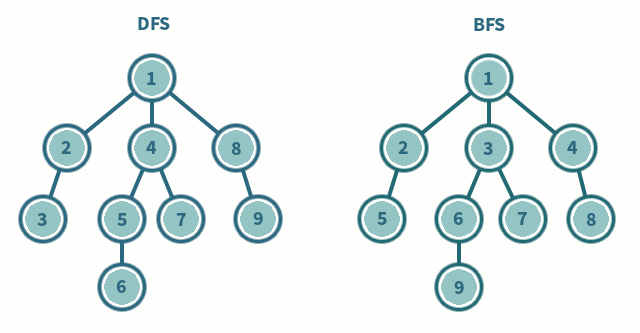
깊이 우선 탐색 - DFS(Depth First Search)
최상위 노드, 특정 노드에서 시작하여 다른 분기로 넘어가기 전에 해당 분기를 완벽하게 탐색하는 방식이다.
즉 한루트로 최대한 깊이 들어가서 확인한 뒤 다음 분기로 넘어가는 탐색 방식이다.
일반적으로 재귀호출을 사용하여 구현하지만 단순한 스택 배열로 구현하기도 한다. (재귀 호출이 복잡하지 않다면 재귀로 짜는것이 개인적으로는 가독성이 더 좋아 재귀를 선호한다.)
사용 케이스
- 미로 탐색 경로를 찾을때
- 모든 노드를 방문해야 하는 문제
- 백트래킹
- 깊이 우선으로 탐색을 하다가 조건에 맞지 않는다면 아래노드를 가지치기 하여 불필요한 탐색을 줄여준다.
장점
- 현재 노드의 경로와 방문 기록만 저장하면 되므로 저장 공간의 수요가 비교적 적다고 할 수 있다.
- 목표 노드가 깊은 단계에 있을 경우 해를 빨리 구할 수 있다.
단점
- 항상 최적의 해를 보장하지 않는다.
- BFS는 노드를 계층별로 탐색하기 때문에 목표 노드를 발견하면 최단 경로가 되지만 DFS는 깊게 들어가서 탐색하기 때문에 더 짧은 경로가 존재할 수 있다.
주의점
- 그래프에서의 무한루프
- 그래프에서 DFS를 사용하는경우 무한 루프에 빠지는 경우가 있을수 있다. 그러므로 방문 노드를 기록하고 다시 방문하지 않도록 해야한다.
- 스택 오버 플로우
- 깊이가 매우 깊은 트리나 그래프에서는 스택 오버 플로우가 일어날수 있다. 이런 상황이 놓인다면 재귀호출을 사용하는 것이 아니고 스택을 이용하는 방식이 좋다. (이정도 문제가 일어나는 경우라면 더 좋은 알고리즘을 선택하거나 잘못된 방식으로 풀고있는 경우가 많다)
너비 우선 탐색 - BFS(Breadth First Search)
최상위 노드에서 이웃노드를 방문하고 그 이웃의 이웃 노드를 방문하는 식으로 탐색 범위를 너비 방향으로 확장해 나가는 방식이다.
일반적으로 Queue를 사용하여 구현한다.
사용 케이스
- 최단 경로를 찾는 문제를 풀때
- 미로 탐색 경로를 찾을때
- DFS, BFS모두 완전탐색이기 때문에 미로 탐색에 사용될 수 있다.
장점
- 최단 경로를 보장한다. (가중치가 없다는 가정하에)
단점
- 넓이가 넓은경우 상위 노드의 데이터를 모두 가지고있기 때문에 DFS에 비해 메모리를 많이 사용할수가 있다.
- 해가 최하단에 있는경우 시간이 오래 걸릴수가 있다.
주의점
- 노드간에 연결성이 있는경우 불필요한 탐색을 진행할수가 있기때문에 방문 노드를 기록해야한다.
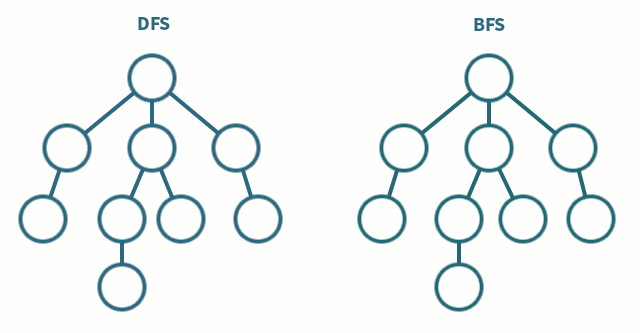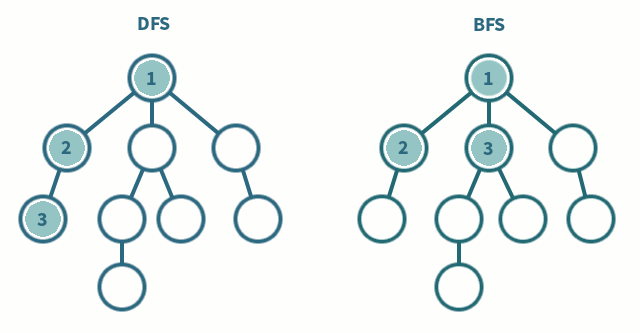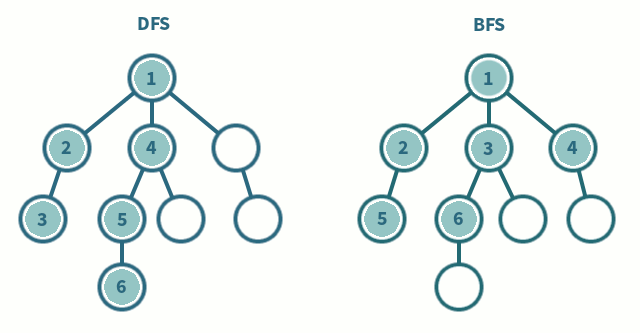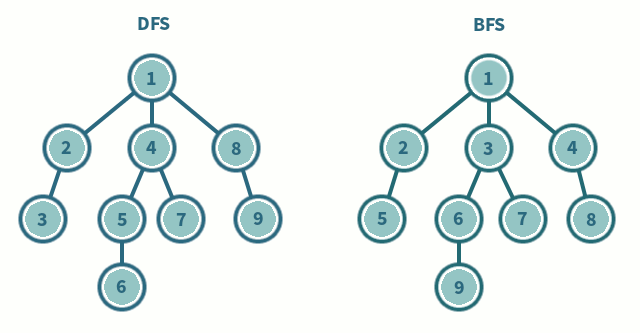
위 사진을 보면 DFS와 BFS의 탐색 순서를 차이를 알 수 있다.
DFS BFS를 익혀둬야 하는 이유
DFS와 BFS가 탐색 알고리즘의 기본이 된다고 생각되는 부분은 탐색 문제의 개발 메커니즘의 이해와 다른 알고리즘을 사용했을때 왜 그 알고리즘이 효율적이고 어느상황에서 써야한다는것을 알게 되기 때문이라고 생각한다.
예를들어 BFS이 가중치가 없는 상황에서 최단거리라고 했지만 가중치가 있는 상황이라면 다익스트라 알고리즘을 사용해야 한다. 다익스트라 알고리즘은 BFS방식에 우선순위 큐를 도입한 BFS확장버전이라고 볼수 있기 때문이다.(완전 같다고 볼수는 없지만...)
dfs와 bfs는 탐색 문제중 아주 기본이 되기때문에 문제 몇개만 풀어보면 간단하게 이해하기 쉬울것이다.
(좋은 문제가 있었던거 같은데 못찾겠음... 찾으면 수정 예정...)
BFS: https://leetcode.com/problems/minimum-depth-of-binary-tree/description/
DFS: https://leetcode.com/problems/path-sum/
사진 출처: https://namu.wiki/w/%EB%84%88%EB%B9%84%20%EC%9A%B0%EC%84%A0%20%ED%83%90%EC%83%89
