문제

https://www.acmicpc.net/problem/2307

---

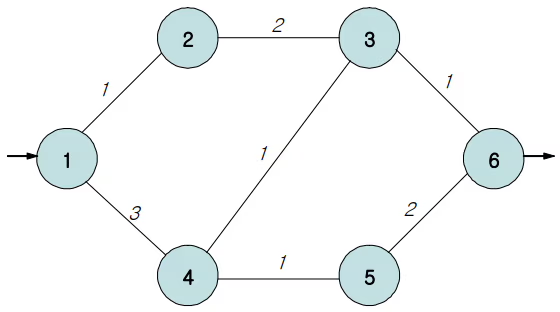
입력

• 지점의 수를 나타내는 정수 N, 도로의 수 M
• M개의 각 줄에는 도로(a, b)와 그 통과시간 t가 a b t 로 표시된다.

---

출력

• 경찰이 하나의 도로를 막음으로써 지연시킬 수 있는 최대 시간을 정수로 출력한다. (단, 그 지연시간이 무한대이면 -1을 출력해야 한다.)

---

풀이

제한조건

• N(6 ≤ N ≤ 1000)
• M(6 ≤ M ≤ 5000)
• a < b 이고 1 ≤ t ≤ 10000

접근방법

다익스트라 응용

문제의 추가설명 4번을 유심히 보자

용의자는 검문을 피해서 가장 빨리 도시를 빠져나가고자 하고, 경찰은 적절한 도로를 선택하여 이 용의자들의 탈출시간을 최대한 지연시키고자 한다.

이 문구를 통해서 용의자는 경찰이 배치되지 않은 경로로 항상 최단거리로 이동한다. 라는 것을 알 수 있다.

경찰은 적절한 도로를 선택하여 이 용의자들의 탈출시간을 최대한 지연시키고자 한다.

라는 말은 조금 생각해보면, 적절한 도로를 선택하여 탈출 시간을 지연시키기 위해서는
당연히 용의자가 최단경로로 이동했던 길 중 하나를 선택하여 막아야 지연이 발생한다는 것을 알 수 있다.

따라서 기본 아이디어를 정리하자면 아래와 같다.

1. 다익스트라를 통해 1->N 까지 최단거리 탐색
	a. 최단거리 탐색과정에서의 경로 기록 필요
2. 최단 거리의 이동 경로를 바탕으로 경찰이 막을 도로 선정
3. 다익스트라를 통해 1->N 까지 최단거리 탐색
4. 지연된 시간 비교

이 문제의 핵심은
당신은 다익스트라를 구현할 수 있습니까? 가 아니라
당신은 다익스트라의 경로를 추출할 수 있습니까? 를 묻는 것이다.

다익스트라의 경로를 찾으려면 어떻게 할 수 있을지 생각해보자.

private static void dijkstra(int start, int end) {
	PriorityQueue<Node> pq = new PriorityQueue<>();
	Arrays.fill(dist, INF);
	dist[start] = 0;
	pq.add(new Node(1, 0));

	while (!pq.isEmpty()) {
		Node cur = pq.poll();
		if (cur.to == end) // 목적지 도달
			break;
		for (Node next : graph[cur.to]) {
			if (dist[next.to] > dist[cur.to] + next.weight) {
				dist[next.to] = dist[cur.to] + next.weight; // 비용 갱신
				pq.add(new Node(next.to, dist[next.to]));
			}
		}
	}
}

일반적으로 다익스크라 구현을 했다면 위와 같은식으로 구현이 된다.
여기서 아이디어를 생각해보자면,
다음 목적지로의 비용을 갱신하는 과정에서 이전에 어디서 왔는지를 기록하면 된다.

private static void dijkstra(int start, int end, int[] disable) {
	PriorityQueue<Node> pq = new PriorityQueue<>();
	Arrays.fill(dist, INF);
	dist[start] = 0;
	pq.add(new Node(1, 0));

	while (!pq.isEmpty()) {
		Node cur = pq.poll();
		if (cur.to == end) // 목적지 도달
			break;
		for (Node next : graph[cur.to]) {
			// 현재 위치에서 다음 위치로 가는길에 검문이 있다. -> 지나갈 수 없음
			if (cur.to == disable[0] && next.to == disable[1])
				continue;
			if (dist[next.to] > dist[cur.to] + next.weight) {
				dist[next.to] = dist[cur.to] + next.weight; // 비용 갱신
				prev[next.to] = cur.to; // 경로 기록
				pq.add(new Node(next.to, dist[next.to]));
			}
		}
	}
}

위와 같은 식으로 기록을 했다면, N번 노드로 가기위해 바로 직전 방문했던 노드가 prev[N]번 노드임을 알 수 있다.

이제 어떤 경로로 이동했는지 파악이 가능하므로, 각 경로를 하나씩 막으면서 다시 다익스트라 알고리즘을 수행하며 거리를 파악하자.

새롭게 산출된 값과 기존의 값을 비교하며 얼마나 지연시킬 수 있는지 확인한다면 끝이다.

---

코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Arrays;
import java.util.List;
import java.util.PriorityQueue;

public class Main {
	static class Node implements Comparable<Node> {
		int to;
		int weight;

		Node(int to, int weight) {
			this.to = to;
			this.weight = weight;
		}

		@Override
		public int compareTo(Node o) {
			return this.weight - o.weight;
		}
	}

	static List<Node>[] graph;
	static int N, M;
	static int[] dist, prev;
	static int INF = 987654321;

	public static void main(String[] args) throws Exception {
		BufferedReader in = new BufferedReader(new InputStreamReader((System.in)));
		String[] inputs = in.readLine().split(" ");
		N = stoi(inputs[0]);
		M = stoi(inputs[1]);

		graph = new List[N + 1];
		for (int i = 0; i <= N; ++i)
			graph[i] = new ArrayList<>();

		for (int i = 0; i < M; ++i) {
			inputs = in.readLine().split(" ");
			int p1 = stoi(inputs[0]);
			int p2 = stoi(inputs[1]);
			int cost = stoi(inputs[2]);
			graph[p1].add(new Node(p2, cost));
			graph[p2].add(new Node(p1, cost));
		}

		dist = new int[N + 1];
		prev = new int[N + 1];
		dijkstra(1, N, new int[] {0, 0});

		// 지나왔던 경로를 바탕으로, 이동할 수 없는 도로를 생성.
		List<int[]> pathList = new ArrayList<>();
		for (int i = N; prev[i] != 0; i = prev[i])
			pathList.add(new int[] {prev[i], i});

		int max = 0;
		int orgTime = dist[N];
		for (int[] path : pathList) {
			dijkstra(1, N, path);
			int fixTime = dist[N];
			// 도시를 빠져나가지 못하게 만들 수 있는 경우
			if (fixTime == INF) {
				max = -1;
				break;
			}
			max = Math.max(max, fixTime - orgTime);
		}
		System.out.println(max);
	}

	private static void dijkstra(int start, int end, int[] disable) {
		PriorityQueue<Node> pq = new PriorityQueue<>();
		Arrays.fill(dist, INF);
		dist[start] = 0;
		pq.add(new Node(1, 0));

		while (!pq.isEmpty()) {
			Node cur = pq.poll();
			if (cur.to == end) // 목적지 도달
				break;
			for (Node next : graph[cur.to]) {
				// 현재 위치에서 다음 위치로 가는길에 검문이 있다. -> 지나갈 수 없음
				if (cur.to == disable[0] && next.to == disable[1])
					continue;
				if (dist[next.to] > dist[cur.to] + next.weight) {
					dist[next.to] = dist[cur.to] + next.weight; // 비용 갱신
					prev[next.to] = cur.to; // 경로 기록
					pq.add(new Node(next.to, dist[next.to]));
				}
			}
		}
	}

	private static int stoi(String s) {
		return Integer.parseInt(s);
	}
}