문제

https://www.acmicpc.net/problem/1654

---

입력

랜선의 개수 K, 그리고 필요한 랜선의 개수 N
각 랜선의 길이

---

출력

첫째 줄에 N개를 만들 수 있는 랜선의 최대 길이를 센티미터 단위의 정수로 출력한다.

---

풀이

제한조건

• K는 1이상 10,000이하의 정수이고, N은 1이상 1,000,000이하의 정수
• 랜선의 길이는 2^31-1보다 작거나 같은 자연수이다.

접근방법

이분탐색

K와 N뿐만 아니라 랜선의 길이로 나올 수 있는 값에 주목해보자.
최대 2^31-1의 수까지 나올 수 있다.

따라서 완전탐색으로 계산한다면, 1부터 2^31-1번 수행하는 과정 중에 우리가 원하는 답을 찾을 수 있다.

하지만 이분 탐색으로 계산을 한다면 어떻게 될까?
(이분탐색 : https://velog.io/@hyeokkr/%EC%9D%B4%EB%B6%84%ED%83%90%EC%83%89)
절반씩 범위를 줄여나갈 수 있으므로 훨씬 짧은 시간에 탐색이 가능하다.

이분 탐색으로 문제를 해결하는 과정을 조금 더 자세히 살펴보자.

탐색의 시작은 위 그림과 같을 것이다.
우리는 이분 탐색을 통해, N개를 만들 수 있는 최대값을 구하고자 한다.
이때, N개를 만들 수 있는 경우는 단 1개 존재할 수 도 있고, 여러개 존재할 수도 있다.

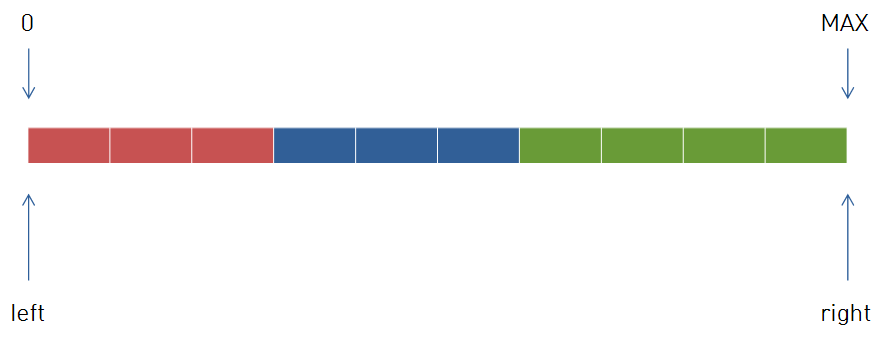
빨간색 범위에 속하는 길이로 자를경우 A개를 만들 수 있고,
파란색 범위의 경우 B개
초록색 범위의 경우 C개를 만들 수 있는 경우.

따라서 우리가 찾고자 하는 지점은 N개를 만들 수 있으면서 가장 오른쪽에 위치한 지점을 찾으면 된다.

이말인즉 이분탐색을 수행하면서 Left와 Right가 계속 갱신이 되는데,
Left가 Right보다 커져서 더 이상 탐색할 수 없는 경우
그때의 Left는 원하는 범위를 1만큼 초과된 지점이다.
따라서 Left - 1로 정답을 구할 수 있다.

---

코드

import java.io.BufferedReader;
import java.io.InputStreamReader;

public class Main {
	static int K, N;
	static long[] arr;

	public static void main(String[] args) throws Exception {
		BufferedReader in = new BufferedReader(new InputStreamReader(System.in));
		String[] inputs = in.readLine().split(" ");
		K = stoi(inputs[0]);
		N = stoi(inputs[1]);

		arr = new long[K];
		for (int i = 0; i < K; ++i)
			arr[i] = stoi(in.readLine());

		long left = 0;
		long right = Integer.MAX_VALUE;

		while (right >= left) {
			long mid = (left + right) / 2;

			long count = 0;
			for (long value : arr)
				count += value / mid;

			if (count >= N)
				left = mid + 1;
			else
				right = mid - 1;
		}
		System.out.println(left - 1);
	}

	public static int stoi(String s) {
		return Integer.parseInt(s);
	}
}