문제

https://www.acmicpc.net/problem/21942

---

입력

• 입력은 최대 1000개의 테스트 케이스로 이루어져 있다
• 입력의 마지막 줄에는 0이 하나 주어진다.

---

출력

• 각 테스트 케이스에 대해서 가능한 문자열의 개수를 출력한다.

---

풀이

제한조건

• 병에 들어있는 약의 개수 N ≤ 30

접근방법

DP

문제를 살펴보면 경우의 수를 묻고 있다.
따라서 우선 정답을 찾기위한 탐색과정을 거쳐야 한다.

또한 여기서 한조각 전체 또는 반조각중 선택을 하게 된다.
2N일 동안 진행하므로 2^60번의 선택을 해야함을 알 수 있다.

알고리즘 문제풀이에서 이 정도의 탐색이 완전 탐색으로 나오는 경우는 없다.
규칙을 찾고 점화식으로 해결해보자.

우선 규칙을 파악하기 위해 단순 나열해보자
문제에서는 W 와 H로 표기되어 있지만, 편의 상 ( 와 )로 대체해서 나열해보자.

N = 1
()

N = 2
(())
()()

N = 3
((()))
(()())
(())()
()(()) 
()()()

N = 4
(((())))
((()()))
((())())
((()))()
(()(()))
(()()())
(()())()
(())(())
(())()()
()((()))
()(()())
()(())()
()()(())
()()()()

뭔가 익숙한 형태로 나온다.

N개의 ()로 이루어진 괄호쌍을 구하는 문제와 동일한 문제임을 알 수 있다.
이는 카탈란 수 문제로 해결할 수 있다.

문제를 생각해봤을때 올바른 괄호쌍을 만드는 수와 동일한 형태의 문제라면
카탈란 수를 바로 적용해보자.

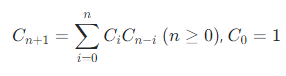
주의
해당 문제의 예시 입력에서 힌트를 얻을 수 있다.
문제에서 % 연산의 결과를 구하는것이 아닌, 수의 크기가 매우 큰 수 임을 알 수 있다.
따라서 type에 따라 overflow 발생을 유의해야한다.

---

코드

import java.io.BufferedReader;
import java.io.InputStreamReader;
import java.math.BigInteger;

public class Main {

	public static void main(String[] args) throws Exception {
		BufferedReader in = new BufferedReader(new InputStreamReader((System.in)));
		StringBuilder sb = new StringBuilder();

		BigInteger[] arr = new BigInteger[31];
		arr[0] = BigInteger.valueOf(1);
		arr[1] = BigInteger.valueOf(1);
		arr[2] = BigInteger.valueOf(2);
		for (int i = 3; i <= 30; ++i) {
			arr[i] = BigInteger.valueOf(0);
			for (int a = 0; a < i; ++a)
				arr[i] = arr[i].add(arr[a].multiply(arr[i - a - 1]));
		}

		while (true) {
			int N = stoi(in.readLine());
			if (N == 0)
				break;
			sb.append(arr[N]).append("\n");
		}
		System.out.println(sb);
	}

	private static int stoi(String s) {
		return Integer.parseInt(s);
	}
}