문제

https://school.programmers.co.kr/learn/courses/30/lessons/67260

---

입력

• 트럭에 실을 수 있는 재활용 택배 상자의 최대 개수를 나타내는 정수 cap
• 배달할 집의 개수를 나타내는 정수 n
• 각 집에 배달할 재활용 택배 상자의 개수를 담은 1차원 정수 배열 deliveries
• 각 집에서 수거할 빈 재활용 택배 상자의 개수를 담은 1차원 정수 배열 pickups

---

출력

• 트럭 하나로 모든 배달과 수거를 마치고 물류창고까지 돌아올 수 있는 최소 이동 거리

---

풀이

제한조건

• n은 2 이상 200,000 이하입니다.
  - path 배열의 세로(행) 길이는 n - 1 입니다.
  - path 배열의 원소는 [방 번호 A, 방 번호 B] 형태입니다.
  - 두 방 A, B사이를 연결하는 통로를 나타냅니다.
• order 배열의 세로(행) 길이는 1 이상 (n / 2) 이하입니다.
  - order 배열의 원소는 [방 번호 A, 방 번호 B] 형태입니다.
  - A번 방을 먼저 방문한 후 B번 방을 방문해야 함을 나타냅니다.

접근방법

BFS 응용

복잡해보이지만 사실 단순 BFS로 풀 수 있다.
문제의 핵심은 선 방문 조건이 있는 그래프의 모든 정점을 갈 수 있는가를
묻는 것이다.

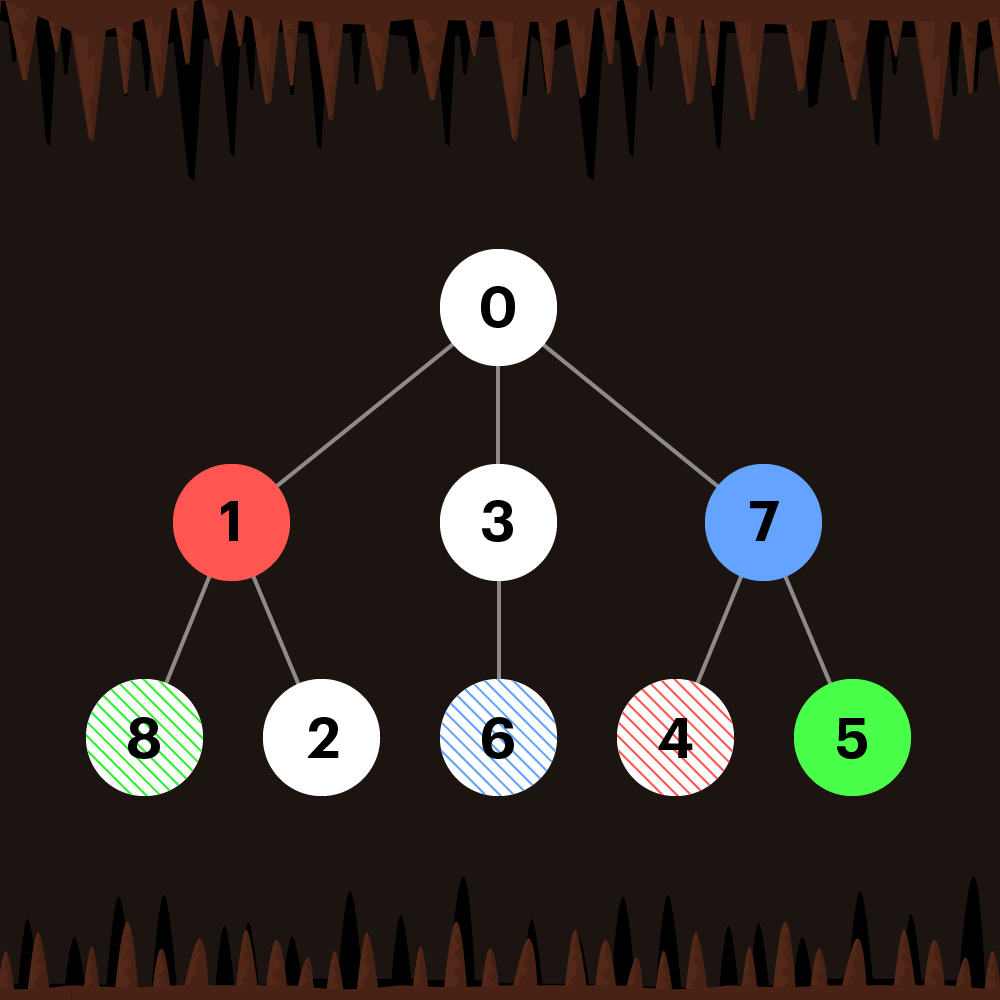
예시로 한 번 살펴보자.

BFS, Step1.
우선 0번 부터 탐색한다.
BFS를 통해 1,3,7번을 탐색할 수 있다.
하지만 1,7의 경우, 선행 방문 정점이 존재한다.
따라서 3번만 큐에 넣어준다.

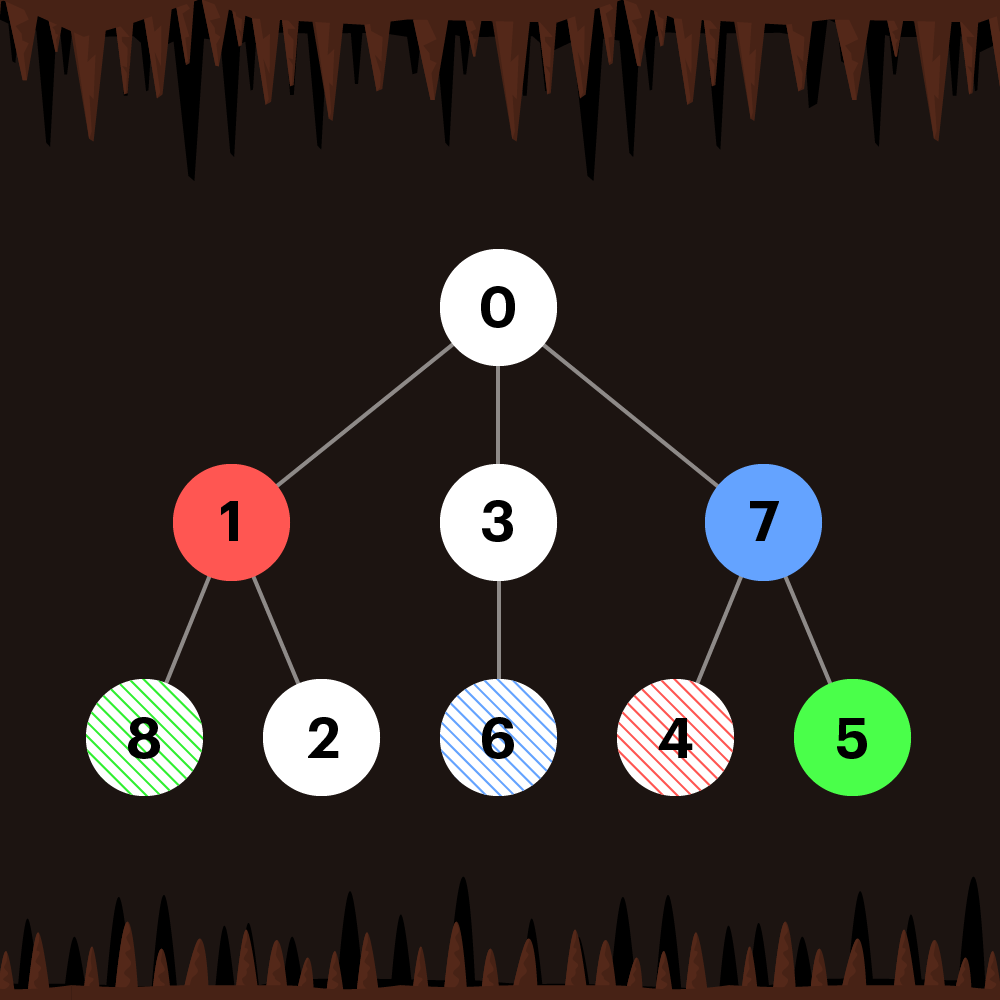
BFS, Step2.
이제 큐에 있는 3번 정점을 탐색해주자.
3번에서는 한 번도 방문하지 않은 6번 정점을 방문 할 수 있다.

BFS, Step3.
이제 6번 정점을 탐색한다.
6번 정점을 방문하게 된다면, 7번 정점을 방문할 수 있는 조건을 만족한다.
여기서 처리를 잘 해야한다.

7번 정점은 앞서 0번에서 갈 수 있는 지점이 었다.
하지만 0번은 BFS에서 큐를 통해 이미 탐색한 지점이다.
어떻게 7번 정점을 BFS 큐에 넣을 수 있을까.

무작정 집어 넣는다면, 뜬금 없는 지점에서부터 다시 탐색하는 경우가 발생한다.
따라서 방문하고자 하는 7번 정점을 기준으로, 인접한 정점 중, 이미 방문한 정점이 있다면, 큐에 넣어주면 된다.

BFS, Step4....
앞으로의 과정은 1~3과정을 반복하면 된다.

요약
1. BFS를 통해 탐색한다.
2. Map을 통해 선행 정점을 기록한다.
3. 방문 체크를 할 2개의 배열을 별도로 생성한다.
	- BFS를 통해 방문한 지점인지 확인
    - 현재 탐색할 수 있는 지점인지 확인

---

코드

import java.util.*;

class Solution {
	List<Integer>[] list;
	boolean[] canVisit;
	Map<Integer, Integer> map = new HashMap<>();

	public boolean solution(int n, int[][] path, int[][] order) {
		list = new List[n];
		canVisit = new boolean[n];
		Arrays.fill(canVisit, true);
		for (int data[] : order) {
			map.put(data[0], data[1]);
			canVisit[data[1]] = false;
		}
		for (int i = 0; i < n; ++i)
			list[i] = new ArrayList<>();

		for (int data[] : path) {
			list[data[0]].add(data[1]);
			list[data[1]].add(data[0]);
		}

		Queue<Integer> q = new ArrayDeque<>();
		boolean[] visit = new boolean[n];
		visit[0] = true;
		q.add(0);
		int count = 1;

		while (!q.isEmpty()) {
			int cur = q.poll();

			for (int next : list[cur]) {
				// 갈 수 있으며, 방문한 적이 없다면 진행
				if (canVisit[next] && !visit[next]) {
					visit[next] = true;
					q.add(next);
					count++;
				}
			}

			// 현재 방을 방문함으로써, 새롭게 열리는 방이 있는 경우
			if (map.containsKey(cur)) {
				int next = map.get(cur);
				canVisit[next] = true;
				for (int check : list[next]) {
					if (visit[check]) {
						visit[next] = true;
						q.add(next);
						count++;
						break;
					}
				}
			}
		}
		return count == n ? true : false;
	}
}