문제

https://school.programmers.co.kr/learn/courses/30/lessons/118669

---

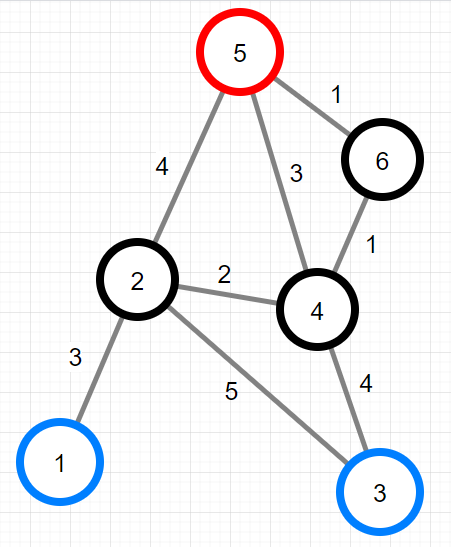
입력

• XX산의 지점 수 n
• 각 등산로의 정보를 담은 2차원 정수 배열 paths
• 출입구들의 번호가 담긴 정수 배열 gates
• 산봉우리들의 번호가 담긴 정수 배열 summits

---

출력

intensity가 최소가 되는 등산코스에 포함된 산봉우리 번호와 intensity의 최솟값

---

풀이

제한조건

• 2 ≤ n ≤ 50,000
• n - 1 ≤ paths의 길이 ≤ 200,000
• 출입구이면서 동시에 산봉우리인 지점은 없습니다.
• gates와 summits에 등장하지 않은 지점은 모두 쉼터입니다.
• 임의의 두 지점 사이에 이동 가능한 경로가 항상 존재합니다.

접근방법

우선순위 큐 + BFS
복잡해보이지만 생각보다 문제는 단순하다.

intensity, 즉 간선의 가중치가 낮은순으로 먼저 살피며 BFS를 순회하면 된다.

BFS에서의 방문지점 체크를 간선의 가중치(intensity)로 기록해두고 탐색을 하며 산봉우리에 도착을 했는지를 확인하면 된다.

1. 우선순위 큐를 사용한다.
	a. 가중치가 낮은 순
    b. 번호가 낮은 순 (가중치가 같다면 낮은 번호의 산봉우리가 정답이므로)
    
2. BFS 탐색
3. 산봉우리 도착여부 확인
	a. 도착했다면, 최대 가중치가 얼마였는지 찾자.

주의해야할 점은 산봉우리에 도착을 했다고 바로 마무리 하면 안된다.

예를들어 아래와 같은 케이스가 있다고 생각해보자.

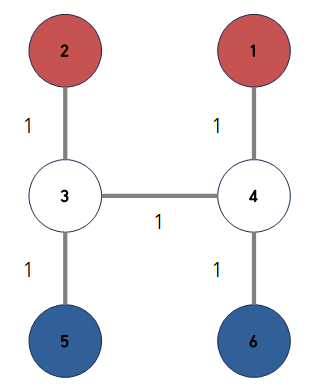
단순한 로직을 구현하였다면

1. 5와 6이 큐에 삽입
2. 낮은 번호인 5에서부터 탐색 
-> 큐에는 3과 6이 남는다.
	(가중치가 모두 같음)
3. 낮은 번호인 3에서 탐색 시작
-> 정답으로 2번 봉우리 탐색완료.

하지만 위의 케이스에서 5-3-4-1 구간으로 가도 동일한 intensity를 가지며 더 낮은 숫자의 봉우리로 갈 수 있다.

따라서 탐색과정에서 봉우리를 만났다면,
바로 종료할 것이 아니라 같은 비용으로 갈 수 있는 다른 봉우리가 있는지 끝까지 탐색하고 종료해야 한다.

---

코드

import java.util.*;

class Node implements Comparable<Node>{
	int from;
	int to;
	int weight;
	Node(int a, int b, int c){
		from = a;
		to = b;
		weight = c;
	}

	public int compareTo(Node o){
		if(this.weight == o.weight)
			return this.to - o.to;
		return this.weight - o.weight;
	}
}
class Solution {
	List<Node>[] graph;
	Set<Integer> start, end;
	int[] dist;
	public int[] solution(int n, int[][] paths, int[] gates, int[] summits) {
		graph = new List[n + 1];
		dist = new int[n + 1];
		for(int i = 0; i <= n; ++i)
			graph[i] = new ArrayList();
		start = new HashSet(); // 출발지
		end = new HashSet(); // 도착지

		for(int i : gates)
			start.add(i);
		for(int i : summits)
			end.add(i);

		for(int[] data : paths){
			if(!start.contains(data[1]) && !end.contains(data[0]))
				graph[data[0]].add(new Node(data[0], data[1], data[2]));
			if(!start.contains(data[0]) && !end.contains(data[1]))
				graph[data[1]].add(new Node(data[1], data[0], data[2]));
		}


		int[] answer = new int[2];
		search(answer);

		return answer;
	}

	public void search(int[] answer){
		Arrays.fill(dist, Integer.MAX_VALUE);
		PriorityQueue<Node> pq = new PriorityQueue();
		for(int i : start){
			for(Node node : graph[i])
				pq.add(node);
		}

        answer[0] = Integer.MAX_VALUE;
        int max = Integer.MAX_VALUE;
		while(!pq.isEmpty()){
			Node cur = pq.poll();
            if(cur.weight > max)
                break;
			dist[cur.to] = cur.weight;

			if(end.contains(cur.to)){
				// 정상에 도착함. 최대값을 찾자.
				for(int value : dist){
					if(value>max && value != Integer.MAX_VALUE || max == Integer.MAX_VALUE)
						max = value;
				}
				answer[0] = answer[0]<cur.to?answer[0]:cur.to;
                //answer[0] =Math.min(answer[0],cur.to);
				answer[1] = max;
			}

			for(int i = 0; i < graph[cur.to].size(); ++i){
				Node next = graph[cur.to].get(i);

				// 다음지점으로 가본적이 없는 경우.
				if(dist[next.to] == Integer.MAX_VALUE) {
					pq.add(next);
				}
			}
		}
	}
}