문제

https://school.programmers.co.kr/learn/courses/30/lessons/12971

---

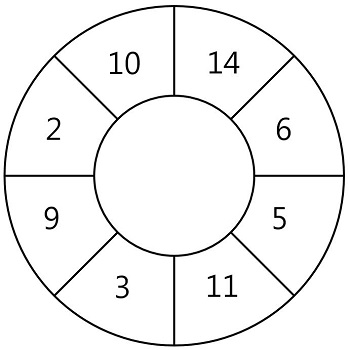
입력

스티커에 적힌 숫자가 배열

---

출력

스티커를 뜯어내어 얻을 수 있는 숫자의 합의 최댓값

---

풀이

제한조건

• sticker는 원형으로 연결된 스티커의 각 칸에 적힌 숫자가 순서대로 들어있는 배열로, 길이(N)는 1 이상 100,000 이하입니다.
• sticker의 각 원소는 스티커의 각 칸에 적힌 숫자이며, 각 칸에 적힌 숫자는 1 이상 100 이하의 자연수입니다.
• 원형의 스티커 모양을 위해 sticker 배열의 첫 번째 원소와 마지막 원소가 서로 연결되어있다고 간주합니다.

접근방법

방법1. 재귀 X
첫번째는 재귀 방식으로 접근하였다.
배열의 구간을 정하고 계산해본다.
함수를 하나 만들고 특정 구간에서 구할 수 있는 최대값을 구하는 방식이다.

아래와 같은 형식으로 접근한다.

int getMax(start, end)
Max(arr[i] + getMax(start+2, end), getMax(start+1, end))

문제는 N이 100,000 까지이고 효율성 체크가 있기때문에 성공할 수 없다.

방법2. DP O
효율성 문제를 해결하기 위한 방법으로 dp를 활용한다.
처음 구현은 아래와 같은 형식으로 접근했다.

dp[i] = max(dp[i-2]+sticker[i] , dp[i-2])

하지만 데이터가 아래와 같이 구성된 경우
5 + 50 으로 최대 결과가 나오지만 위의 식에서는 계산할 수없다.

sticker = {5,6,7,50,6}

따라서 조금의 수정과 문제 조건(처음과 마지막이 연결되어있음)을 반영해 아래 정답코드와 같이 수정하여 최대값을 찾았다.

---

코드

import java.util.*;
class Solution {
	public int solution(int sticker[]) {
		int len = sticker.length;

        if(len == 1)
            return sticker[0];
        if(len == 2)
            return Math.max(sticker[0], sticker[1]);
        
		int[][] arr = new int[2][len + 1];

		// Step1. 첫번째 스티커를 포함하는 경우
		arr[0][0] = sticker[0];
		arr[0][1] = Math.max(sticker[0], sticker[1]);

		for (int i = 2; i < len - 1; ++i) {
        // i-2의 값이 i-1보다 크다면, i-2 값에 현재 스티커를 뜯는게 가장 크다.
			if (arr[0][i - 2] > arr[0][i - 1]) {
				arr[0][i] = arr[0][i - 2] + sticker[i];
			} else {
            	// i-1의 값이 i-2에 i번째 스티커를 뜯은것 보다 클 경우
				if (arr[0][i - 1] > arr[0][i - 2] + sticker[i]) {
					arr[0][i] = arr[0][i - 1];
				} else {
					arr[0][i] = arr[0][i - 2] + sticker[i];
				}
			}
		}

		// Step2. 마지막 스티커를 포함하는 경우
		arr[1][1] = sticker[1];
		arr[1][2] = Math.max(sticker[1], sticker[2]);

		for (int i = 3; i < len; ++i) {
			if (arr[1][i - 2] > arr[1][i - 1]) {
				arr[1][i] = arr[1][i - 2] + sticker[i];
			} else {
				if (arr[1][i - 1] > arr[1][i - 2] + sticker[i]) {
					arr[1][i] = arr[1][i - 1];
				} else {
					arr[1][i] = arr[1][i - 2] + sticker[i];
				}
			}
		}

		// Step3. 위의 두 케이스 중 가장 큰값이 정답이다.
		return Arrays.stream(arr).flatMapToInt(Arrays::stream).max().getAsInt();
	}
}