문제
https://school.programmers.co.kr/learn/courses/30/lessons/92343
입력
- 각 노드에 있는 양 또는 늑대에 대한 정보가 담긴 배열 info
- 2진 트리의 각 노드들의 연결 관계를 담은 2차원 배열 edges
출력
- 각 노드를 방문하면서 모을 수 있는 양은 최대 몇 마리인지 return
풀이
제한조건
- 2 ≤ info의 길이 ≤ 17
- info의 원소는 0 또는 1 입니다.
- info[i]는 i번 노드에 있는 양 또는 늑대를 나타냅니다.
- 0은 양, 1은 늑대를 의미합니다. - 항상 하나의 이진 트리 형태로 입력이 주어지며, 잘못된 데이터가 주어지는 경우는 없습니다.
접근방법
DFS 변형
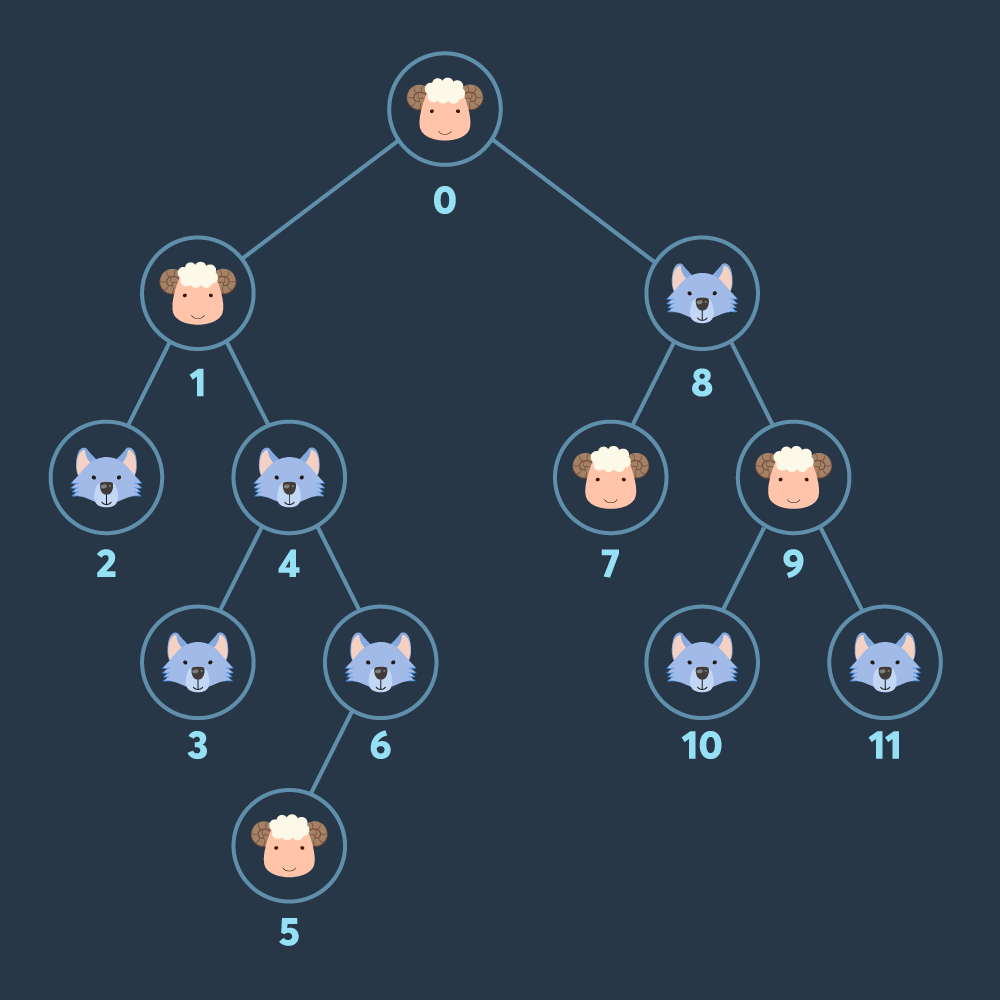
예제를 통해 최선의 경우를 살펴보자.
0-1-8-7-9-4-6-5 순으로 이동한다면 최대 5마리의 양을 모을 수 있다.
위와 같이 최선의 순서로 탐색하려면 어떤 방법이 있을까?
일반적인 탐색이라고 한다면, DFS 또는 BFS를 떠올릴 수 있다.
일반적인 DFS는 0->1->2 ... 또는 0->1->4... 모두 탐색하고 0->8의 순서로 탐색했다.
또한 일반적인 BFS의 경우, 가장 가까운 노드부터 탐색하기에 0-1-8-7-9와 같은 순서를 만들어 내지 못한다.
어떤식으로 조정해야 탐색이 가능할지 충분히 생각해보자.
문제에서 항상 하나의 이진 트리 형태로 주어진다는 점을 이용해보자.
단방향 그래프로 트리를 표현할 수 있다.
그럼 DFS를 조금 변형해서 재귀적으로 탐색해보자.
일반적인 DFS처럼 Depth를 깊게 들어가는것이 아닌, 현재 시점에서 방문할 수 있는 node 를 정하고, 해당 node를 재귀적으로 방문하는 것이다.
예시를 기반으로 따라가보자.
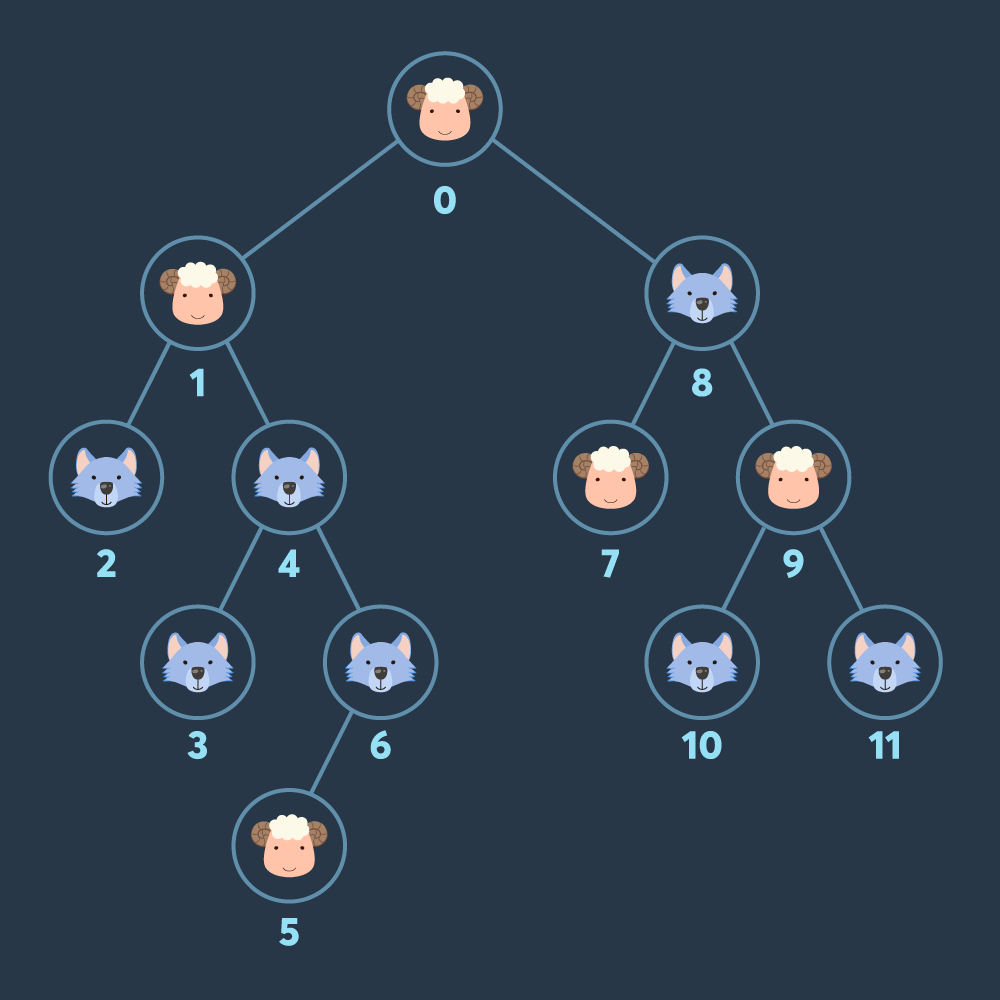
1. 0번노드 탐색.
0번 노드에서 시작을 한다.
그럼 갈 수 있는 노드는 1번과 8번자리가 있다.
갈 수 있는 노드 = {1,8}
여기서 1번 노드를 먼저 탐색해보자.
2. 1번 노드 탐색.
1번 노드를 탐색하면서 기존에 탐색할 수 있던 8번 노드에 추가적으로
1번 노드에서 이동할 수있는 2,4번 노드가 추가되었다.
재귀적인 방법을 통해 각 노드를 모두 방문해준다.
이때, 2또는 4번 노드로 진행한다면, 추가적으로 양을 모을 수 없다.
따라서 모은 양의 최대는 2로 고정된다.
하지만 8번 노드로 간다면 달라진다.
갈 수 있는 노드 = {2,4,8}
3. 8번 노드 탐색.
8번 노드에서는 7, 9번노드로 이동할 수 있다.
갈 수 있는 노드 = {2,4,7,9}
여기까지 했다면, 이제 같은 내용이 반복되는것을 알 수 있다.
양의 수와 늑대의 수를 체크하며 어디가 방문할 수 있는 지점인지 확인하며 탐색을 이어나가자.
함수가 시작될 때, 인자로 넘겨받은 양의 수 중 최대가 이동하며 구할 수 있는 양의 최대 마리수이다.
요약
1. 재귀적으로 탐색한다.
2. 갈 수 있는 node의 번호를 관리할 것.
3. 양의 수와 늑대의 수를 체크하며, 적당한 가지치기를 할 것.코드
import java.util.*;
class Solution {
boolean[] visit;
List<Integer>[] list;
int[] infos;
int answer = 0;
int len;
public int solution(int[] info, int[][] edges) {
len = info.length;
visit = new boolean[len];
list = new List[len];
infos = info;
for (int i = 0; i < len; ++i)
list[i] = new ArrayList<>();
for (int[] edge : edges)
list[edge[0]].add(edge[1]);
for(int next : list[0])
visit[next] = true;
// 재귀로 탐색
simulation(1, 0);
return answer;
}
private void simulation(int sheep, int wolf) {
answer = Math.max(answer, sheep);
for (int i = 1; i < len; ++i) {
// 방문할 수 있는 곳인지 체크(트리의 연결된 지점 중 하나인지)
if (visit[i]) {
visit[i] = false;
// 양인 경우
if (infos[i] == 0) {
for (int next : list[i])
visit[next] = true;
simulation(sheep + 1, wolf);
for (int next : list[i])
visit[next] = false;
} else { // 늑대
// 늑대가 양의 수와 같아지는 순간 먹힌다 -> 탐색할 필요가 없다.
if (sheep > wolf + 1) {
for (int next : list[i])
visit[next] = true;
simulation(sheep, wolf + 1);
for (int next : list[i])
visit[next] = false;
}
}
visit[i] = true;
}
}
}
}