문제
https://school.programmers.co.kr/learn/courses/30/lessons/72413
두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 가정할 때, 최저 예상 택시요금을 계산해서 return
입력
n,s,a,b과 요금 정보
출력
두 사람이 s에서 출발해서 각각의 도착 지점까지 택시를 타고 간다고 가정할 때, 최저 예상 택시요금을 계산해서 return
풀이
제한조건
- 지점갯수 n은 3 이상 200 이하인 자연수입니다.
- 지점 s, a, b는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다.
즉, 출발지점, A의 도착지점, B의 도착지점은 서로 겹치지 않습니다. - fares는 2차원 정수 배열입니다.
- fares 배열의 크기는 2 이상 n x (n-1) / 2 이하입니다.
예를들어, n = 6이라면 fares 배열의 크기는 2 이상 15 이하입니다. (6 x 5 / 2 = 15) - fares 배열의 각 행은 {c, d, f} 형태입니다.
c지점과 d지점 사이의 예상 택시요금이 f원이라는 뜻입니다.
지점 c, d는 1 이상 n 이하인 자연수이며, 각기 서로 다른 값입니다. - 요금 f는 1 이상 100,000 이하인 자연수입니다.
fares 배열에 두 지점 간 예상 택시요금은 1개만 주어집니다. 즉, {c, d, f}가 있다면 {d, c, f}는 주어지지 않습니다.
출발지점 s에서 도착지점 a와 b로 가는 경로가 존재하는 경우만 입력으로 주어집니다.
접근방법
문제를 차근차근 살펴보자.
문제를 읽고 아래의 예시를 봤을 때 각 지점 간의 이동 비용이 제시되어 있고, 최소 비용을 구해야한다.
라는 생각과 동시에 다익스트라...와 같은 알고리즘들을 우선 떠올려보자.
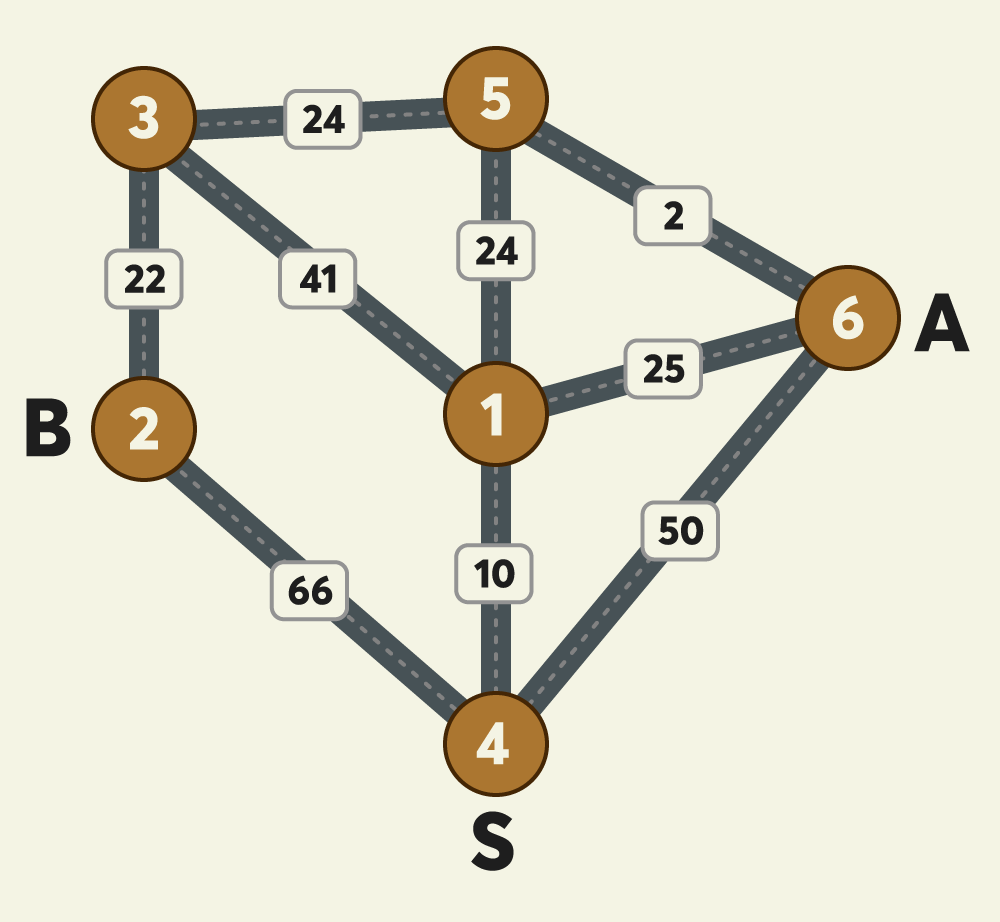
이후, 문제를 다시 한 번 읽어보며 조건들과 주의할 점을 정리해보자.
- 2명(무지, 어피치)는 s에서 출발하여 각자 A, B 지점으로 가야한다.
- 2명(무지, 어피치)의 이동 비용의 합이 최소가 되어야 한다. 처음 생각하기에는 다익스트라로 비용을 구하고, 겹치는 구간에 대해서 합승 처리해야겠다. 라고 생각하였으나, 빠지는 부분이 많아 다른 방법을 생각해야 했다.
조건을 다시 보며, n이 최대 200이므로, N^3으로 해도 1초 안에 처리될 것으로 예상되었다.
플로이드-워셜을 사용하기로 했다.
그래프 내에서 특정 지점 2개를 이동할 수 있는 최단 비용을 모두 계산한 뒤 다시 생각해보면
각자 바로 가는 경우
dist[s][a] + dist[s][b]특정 지점까지 합승하는 경우
dist[s][k] + dist[k][a] + dist[k][b];편하게 구할 수 있다.
특정 지점을 모든 정점으로 두고 순회하면 끝이다.
코드
- 연결리스트
class Solution {
final int INF = 9999999;
int dist[][];
public int solution(int n, int s, int a, int b, int[][] fares) {
dist = new int[n+1][n+1];
for(int i = 1; i <= n; ++i){
for(int j = 1; j <=n; ++j){
if(i==j)
dist[i][j] = 0; // a->a로 가는 경우는 비용이 0
else
dist[i][j] = INF; // a->b로 가는 경우에 관한 비용은 아직 알 수 없음
}
}
// 주어진 요금 정보를 기록
for(int[] data: fares){
// data = {a,b,c} 형식
// a->b, b->a의 요금은 c원
dist[data[0]][data[1]] = data[2];
dist[data[1]][data[0]] = data[2];
}
// 플로이드워셜
for(int k = 1; k <= n; ++k){
for(int i = 1 ; i <= n; ++i){
for(int j = 1 ; j <= n; ++j){
if(dist[i][j] > dist[i][k] + dist[k][j])
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
// 각자 따로가는 비용보다 더 비싼 경우는 없다.
int answer = dist[s][a] + dist[s][b];
// 특정 구간까지 합승해서 갔을 때, 더 싼 경우가 있는지 확인해 본다
for(int i = 1; i <= n; ++i){
answer = Math.min(answer, dist[s][i] + dist[i][a] + dist[i][b]);
}
return answer;
}
}