Clustering

‍이세현·2024년 4월 3일

Unsupervised Learning

Supervised Learning Training set: ${(x^{(1)}, y^{(1)}), (x^{(2)}, y^{(2)}), ..., (x^{(i)}, y^{(i)})}$
Unupervised Learning Training set: ${x^{(1)}, x^{(2)}, ..., x^{(i)}}$

Clustering

Cluster를 선택하는 이유

Labeling은 비용이 드는 작업이다.
data의 분포, 구조와 같은 특성을 얻기 위함이다.
data의 prototypes를 알기 위함이다.

Goal of Clustering

군집 간 유사도는 낮아야 한다.
군집 내의 유사도는 커야 한다.

유사도를 측정하는 measure가 정의되어야 한다.
data에 맞추어 적절한 clustering algorithm을 정해야 한다.
- data의 평가 척도가 애매하기 때문에 Clustering은 매우 주관적이다.

Two Types of Clustering

Hierarchical algorithms: 특정 기준으로 object 집합의 계층적 구분을 생성한다.
Partitional algorithms: 다양한 partition을 구성한 후에 어떤 기준에 따라 평가한다.

Similarity

Similarity(유사도)를 정의하는 것 또한 어려운 문제이다.
- 유사도가 정의가 되면 좋고 나쁨을 판단할 수 있다.
- $D(O_1, O_2)$ : object $O_1$ 과 $O_2$ 사이의 distance(= dissimilarity)
Distance measure의 특성
- Symmetry: $D(A, B) = D(B, A)$
- Constancy of Self-Similarity: $D(A, A) = 0$
- Positivity(Separation): $D(A, B) = 0, \text{if } A=B$
- Triangular Inequality: $D(A, B) \leq D(A, C) + D(B, C)$

A generic technique for measuring similarity

두 object 간의 similarity를 측정하기 위해서는 object a를 b로 바꿀 때 얼마나 변환해야 하는지(measure of effort) 측정한다.
- measure of effort가 distance measure가 된다.
- edit distance 또는 transformation distance라고 부른다.

Hierarchical algorithms

단계적으로 진행하며 distance 판단이 쉽다.

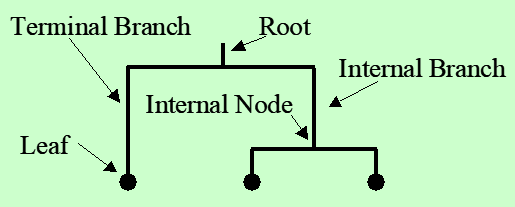
Dendrogram

Dendrogram: 측정한 유사도를 요약하는 도구

Dendrogram에서 두 객체 간의 유사도는 그들이 공유하는 가장 낮은 내부 노드의 높이로 표현된다.
element끼리 비교해야하기 때문에 시간 소요가 크다.
때로 의미 없거나 가짜의 패턴을 보여줄 수 있다.
cluster 개수를 명확하게 구할 수 있다.
- level의 길이를 distance로 볼 수 있다.
- outliers(이상치, 특이점) 검출이 용이하다.
n개의 leaf가 있을 때 가능한 dendrogram 경우의 수 $\frac{(2n-3)!}{2^{(n-2)}(n-1)!}$

Bottom-Up(agglomerative)

일반적인 방법

각 데이터가 모두 나뉘어 있는 상태에서 새로운 cluster로 merge
모든 cluster가 결합될 때까지 반복한다.

Example

(distance measure는 이미 있다고 가정)

	a	b	c	d	e
a	0	8	8	7	7
b		0	2	4	4
c			0	3	3
d				0	1
e					0

가능한 모든 결합을 고려하여 최적을 선택한다.
- 가장 유사한 d와 e를 결합한다.
- 다음으로 유사한 b와 c를 결합한다.
- 반복하여 진행한다.
한 번 group을 결정하면 group 간 distance를 계산하는 measure도 필요하다.
(group - element), (group - group), (element- element) measure 모두 정의해야 한다.
- Single linkage(nearest neighbor): 서로 다른 cluster의 모든 데이터 간 거리 중 최댓값을 선택한다.
- Complete linkage(furthest neighbor): 서로 다른 cluster의 모든 데이터 간 거리 중 최댓값을 선택한다.
- Group average linkage: 서로 다른 cluster의 모든 데이터 간 거리의 평균을 선택한다.
- 사용한 distance measure에 따라 다른 dendrogram이 도출된다.

Top-Down(divisive)

모든 데이터는 하나의 cluster에서 시작된다.
cluster를 두 갈래로 나누는 모든 방법을 고려한다.
최적의 division을 선택하고 양쪽에서 같은 계산을 반복한다.

Hierarchical Clustering Methods Summary

Cluster의 개수를 미리 정할 필요가 없다.

일부 domain에서 hierarchical nature maps는 인간의 직관과 잘 맞는다.

잘 확장되지 않는다

데이터가 $n$ 개일 때 시간 복잡도는 최소 $O(n^2)$ 이다.

모든 element끼리 비교해야 하기 때문

Heuristic search algorithms처럼 local optima가 문제이다.

가능한 모든 클러스터링 구성을 평가하는 대신 일련의 단계를 따라 cluster를 형성하므로 local optima에 빠질 수 있다.

cluster를 형성하는 초기 단계에서 시작 cluster를 선택하거나 각 단계에서 병합 또는 분할을 결정할 때 발생할 수 있습니다.

결과의 해석은 매우 주관적이다.

Partitional algorithms

계산이 빠르다.

각 instance는 정확히 K개의 중복되지 않는 cluster 중 하나에 배치된다.
Cluster는 하나의 set만 출력되기 때문에 사용자는 보통 원하는 개수의 K를 설정해야 한다.

Squared Error

se_{K_i} = \sum_{j=1}^{m}{||t_{ij}-C_k||}^2 se_{K_i} = \sum_{j=1}^{k}{se_{K_j}}

$t_{ij}$ : elements (좌표)
$C_k$ : centroid (좌표)

Distance metric: euclidean distance

K-means

군집의 수 k를 설정한다.
- K가 클수록 데이터의 개수와 가까워지므로 cost는 작아질 수밖에 없다.
- $K$ 에 대한 cost 그래프를 그렸을 때 elbow point를 최적으로 $K$ 로 결정한다.
Cluster center 좌표 k개를 (임의로) 설정한다.
- $K < n$
- 초기 centeroid point에 따라 결과가 달라진다.
N개의 데이터 각각 가장 가까운 cluster center에 할당하여 class를 결정한다.
각 군집에 데이터가 올바르게 할당되었는지 측정하여 cluster center k개를 다시 설정한다.
- cost function: $J(c^{(1)}, ..., c^{(n)}, \mu_1, ..., \mu_K)$
  - gradient descent 가능
마지막 반복에서 각 데이터에 할당된 class가 변하지 않았다면 반복을 종료한다.

Comments on K_means

Strengths

시간복잡도: $O{(tkn)}$ , normally $k, t << n$

$n$ : object의 수

$k$ : 군집의 수

$t$ : 반복 횟수

local optimum에 빠지면 종료한다.

Weakness

평균을 정의할 수 있을 때에만 적용 가능하다.

평균의 계산할 수 없는 categorical data의 경우 부적절하다.

Cluster의 개수 k를 미리 정해야 한다.

noisy data, outliers에 대응할 수 없다.

non-convex shapes는 non-euclidean으로, cluster를 찾기 부적절하다.