EM Algorithm

Clustering

Clustering

• K개의 Clusters $C_1, C_2, \cdots, C_K$가 있고 각 평균은 $m_1, m_2, \cdots, m_K$이다.
• Least-Squares Error는 다음과 같이 정의된다.
  $D=\sum_{k=1}^{K}\sum_{x_i\in C_k}\|x_i - m_k\|^2$
• K개의 클러스터로 가능한 모든 partition 중에 D를 최소화하는 것을 선택한다.

K-Means - Color Clustering

$n$ 차원의 vectors set을 군집화하는 과정

1. Iteration Count $ic$를 1로 설정한다.
2. $K$개의 평균 값 $m_1(1), \cdots, m_k(1)$을 임의로 정한다.
3. 각 벡터 $x_i$에 대해 거리 $D(x_i, m_k(ic))$를 계산하고 $x_i$를 $C_j$에 할당한다.
4. $m_1(ic), \cdots, m_K(ic)$를 업데이트한다.
5. $C_k(ic)와 C_k(ic+1)$이 동일해질 때까지 3번과 4번 과정을 반복한다.

K-Means Classifier

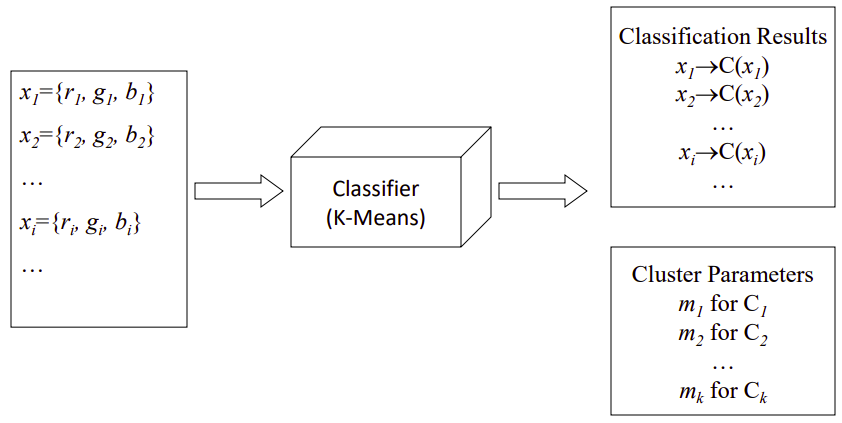
• Input(Known)
  $x_1, x_2, \cdots, x_N$
• Output(Unknown)
  • Cluster Parameters
    $m_1$ for $C_1, \cdots, m_k$ for $C_k$
  • Classification Results
    $x_1 \rightarrow C(x_1)$

Cluster Parameters와 Classification Results가 반복적으로 업데이트된다.

• Boot Step: Initialize $K$ clusters
• Interation Step: Re-estimate te cluster parameters

Image Segmentation by K_Means

K-Means Challenges

• 언젠가는 수렴한다.
• Global Minimum이 아닐 수도 있다.
• Variations: 적절한 cluster 개수를 구하기 위해 k별로 비교해야 한다.

K-Means Variants

• 가장 처음 means를 초기화하는 방법
• 반복을 중단하는 임계
• 주어진 이미지에서 가장 적절한 K를 찾는 다양한 방법

EM Algorithm

확률적 K-Means

• Soft Assignment K-means라고 할 수 있다.

  • Hard Assignment인 K-Means와 차이점
  • K-Means는 가장 가까운 곳에 반드시 매칭한다.

• 확률을 기반으로 각 point를 cluster에 할당한다.

• 가중치합을 계산한다.

• Data $x$와 Clusters $C_1, C_2, C_3$이 있을 때

  • $P(C_1|x)=0.3, P(C_2|x)=\cdots, P(C_3|x)=\cdots$

  • 확률 모델 $P$를 modeling 한다.

    특징	K-Means	EM
    Cluster Representation	mean	mean, variance, weight
    Cluster Initialization	randomly select K means	initialize K Gaussian distributions
    Expectation	assign each point to closest mean	soft-assign each point to each distribution
    Maximization	compute means of current clusters	compute new params of each distribution

Normal distribution

1. 1D case
   1D normal (Gaussian) distribution with mean and standard deviation $\sigma$
   $N(\mu, \sigma)$
2. Multi-dimensional case
   multivariate Gaussian distribution with mean and covariance matrix $\Sigma$
   $N(\mu, \Sigma)$

K-Means $\rightarrow$ EM with Gaussian Mixture Model

The Intuition (1)

각 pixel을 hard하게 하나의 class로 정하는 것보다 확률 이론을 이용하여 확률적으로 정한다.

• 조건부 확률 $p(\hat{y}|\theta)$: 모델이 주어졌을 때 Data가 나타날 확률
• 베이즈 법칙
  $p(C_l|x)=\frac{p(x|C_l)p(C_l)}{\sum_{i=1}^{l}p(x|C_i)p(C_i)}$
  • Posterior: Data $x$가 어떠한 Cluster에 속하는가
  • Likelihood: Cluster가 주어졌을 때 $x$가 나올 확률
  • Prior: 해당 cluster 빈도 - 알 수 있는 값
  • Data가 어느 class인지 알기 위해 모델링이 된 상태에서 Data 확률

The Intuition (2)

• 픽셀을 Cluster Color에 할당할 때 픽셀의 분포(likelihood)
  $p(x|Color)=\mathcal{N}(x|\mu,\Sigma)$

The Intuition (3)

Gaussian 분포로 color distribution을 모델링하지 않고 가중치 합을 구한다. (Posterior)

• $\pi$는 weight, prior이다.
• $p(C_l|x)$를 최대화하는 prior, mean, covariance를 찾아야 한다.
• Masimum Likelihood Estimation을 통해 parameter를 추정해야 한다.

EM with Gauissian Mixture Models

• Boot Step
  • K clusters와 각각의 분포($\mu, \Sigma$), $P(C)$를 초기화 한다.
• Interation Step
  1. Expectation
     • 각 Data의 Cluster 할당을 추정한다.
     • $p(C_j|x_i)$
  2. Maximization
     • 모든 Cluster에 대해 parameters($\mu, \Sigma, p(C)$)를 다시 추정한다.