지역 특징 검출

지역 특징 검출의 기초

특징 검출의 역사

• 무엇을 특징점으로 쓸 것인가?
  • 에지의 경우 차선 인식에서 매우 효율적이지만 에지는 강도와 방향 정보만 가지므로 매칭에 참여하기에는 턱없이 부족하다.
• 다른 곳과 두드러지게 달라 풍부한 정보 추출이 가능한 곳
  • 에지 토막에서 곡률이 큰 지점을 코너로 검출하는 방법
    • 코너 검출의 경우 2000년대 이후 더 좋은 대안이 떠올랐기 때문에 사라졌다.
  • 지역 특징이라는 새로운 물줄기
    • 명암 영상에서 직접 검출이 가능하다.
    • 코너의 물리적 의미: 반복성

지역 특징의 성질

• 지역 특징: <위치, 스케일, 방향, 특징 벡터>$=((y,x), s, \theta, \mathbf{x})$
  • 검출 단계: 위치와 스케일을 알아낸다.
  • 기술 단계: 방향과 특징 벡터를 알아낸다.
• 지역 특징이 만족해야 할 특성
  • 반복성: 항상 그 특성을 유지한다.
  • 분별력: 주변 영역에서 눈에 띄고 두드러져야 한다.
  • 지역성: 그 지역을 대표한다.
  • 정확성
  • 적당한 양: 너무 많으면 계산이 비효율적이다.
  • 계산 효율
• 이들 특성은 길항 관계(동시 작용 시 상쇄)로 응용에 따라 적절한 특징을 선택해야 한다.

지역 특징 검출 원리

• 원리
  • 인지 실험: 사람에게 대응점을 찾기 쉬운 점은 컴퓨터에게도 쉽다.
  • 좋은 정도를 수량화 하는 방법
    • 여러 방향으로 밝기 변화가 나타나는 곳일수록 높은 점수
    • 코너: 여러 방향으로 밝기 변화가 나타나는 곳
• 코너 검출의 기본 아이디어: 명암 차이가 가장 큰 영역
  • 작은 윈도우를 사용해서 방향 별로 명암 차이 계산
    • Flat: 어느 방향에서도 밝기 변화가 없다.
    • Edge: Edge 방향으로는 밝기 변화가 없다.
    • Corner: 모든 방향에서 밝기 변화가 있다.

이동과 회전에 불변한 특징점 검출

모라벡 알고리즘

• 인지 실험에 주목한 모라벡 - 제곱차의 합으로 밝기 변화 측정
  • $S(v, u)=\sum_y\sum_xw(y,x)(f(y+v,x+u)-f(y,x))^2$
    • $w$는 weight
• 출력된 $S$ 맵
  • 코너에서는 모든 방향으로 변화가 나타난다.
  • 에지에서는 에지 방향으로 변화가 적지만 에지에 수직 방향으로 변화가 나타난다.
  • Flat에서는 모든 방향으로 변화가 적다.
  • 코너에는 높은 값, Flat에는 아주 낮은 값을 부여하는 함수를 만들면 된다.
• 모라벡의 함수
  • 특징 가능성 값 $C$
    • $C=\min(S(0,1),S(0,-1), S(1,0), S(-1,0))$
    • 한 점으로부터 오른쪽, 왼쪽, 아래, 위 방향으로 명암값 차이를 계산했을 때 최솟값이 $0$이면 Edge이거나 Flat이고 $C>0$이면 코너일 가능성이 크다.
  • 한계
    • 한 화소만큼 이동하여 네 방향만 본다.
    • 잡음에 대한 대처 방안이 없다.

해리스 코너

• 해리스의 접근 - 가중치 제곱차의 합을 이용한 잡음 대처
  • $S(v,u)=\sum_y\sum_xG(y,x)(f(y+u,x+v)-f(y,x))^2$
    • $G$는 smooth 효과
    • 모라벡의 마스크를 중심에서 멀어질수록 서서히 값이 작아지는 가우시안 마스크로 대체
    • 한 화소 단위로 변화를 살피는 모라벡과 달리 미분을 도입했다
  • $v, u$를 작은 값으로 가정하고 테일러 확장을 대입하면
    $S(v,u)\cong\sum_y\sum_xG(y,x)(vd_y(y,x)+ud_x(y,x))^2$
    
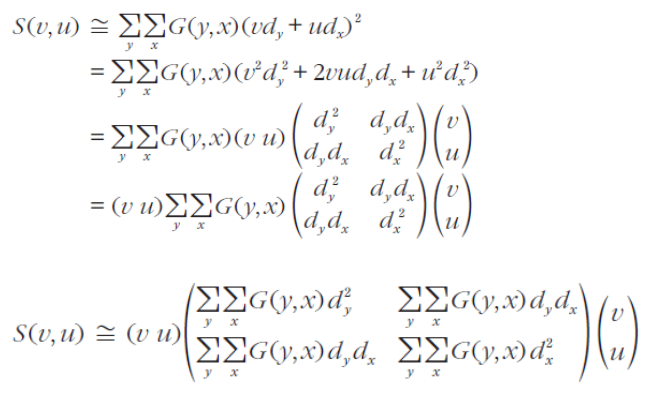
  • 2차 모멘트 행렬 $\mathbf{A}$
    • $S(v,u)=\mathbf{uAu}^T$
    • $(v, u)$와 무관하게 $\mathbf{A}$를 구할 수 있다.
• 통계 관점으로 해석하면 $x$축, $y$축 명암차의 산포(분산, 공분산)이 클수록 코너점에 가깝다.
  • ${I_x}^2, {I_y}^2$이 크면 여러 방향으로 변화가 있는 지점이므로 특징점으로 적합하다.
  • ${I_x}^2$ 또는 ${I_y}^2$ 한 방향으로 변화가 있는 에지이다.
  • $I_xI_y$ 값은 에지의 방향을 나타낸다.
    • 양수이면 양의 상관관계, 음수이면 음의 상관관계
• 선형대수 관점으로 해석하면 eigenvalue, eigenvector
  • 두 개의 Eigenvalue 모두 큰 값이면 특징점으로 적합하다.
  • 두 개의 고유값 중 하나만 크고 다른 하나는 작으면 에지이다.
  • 두 고유값 모두 0에 가까우면 Flat 영역이다.
• 특징 가능성 값 측정
  • $C=\lambda_1\lambda_2-k(\lambda_1+\lambda_2)^2$
• 실제 디지털 영상은 이산적이기 때문에 모든 점을 corner로 오인할 수 있으나 이는 SIFT로 해결할 수 있다.
• 조명에 민감하지만 전반적으로 조명과 무관하다.
• 회전과 이동에 강력하지만 스케일 변화에 민감하다.

스케일에 불변한 특징점 검출

• 거리에 따른 스케일 변화
  • 멀면 작고 윤곽만 어렴풋이 보이다가, 가까워지면 커지면서 세세한 부분이 보인다. 산꼭대기 이미지의 경우 꼭짓점이 특징점으로 보이지만 확대하면 에지로 검출될 수 있다.
• Types of invariance
  • Illumination: 조명 환경의 변화 - Harris의 약점
  • Scale - Harris의 약점
  • Rotation
  • Affine

스케일 공간

• 다중 스케일 영상을 구현하는 두 가지 방식
  1. 가우시안 스무딩: 스케일에 해당하는 $\sigma$가 연속 공간에 정의된다.
  2. 피라미드: 스케일이 절반씩 줄어드는 영상들의 집합(Pyramid image, 다해상도 영상)
     • $\frac{1}{2}$씩 줄어들기 때문에 이산적인 단점이 있다.
• 다해상도 영상에서 공통적으로 검출되는 특징이 Scale 변화에 강한 특징이다.
• 단점: 다해상도 영상 모두 있어야 한다.
  • $\sigma$의 개수 $\times$ 다해상도 영상 개수
  • 성능은 좋아질 수 있으나 시간 소모가 커진다.
• 가우시안 스무딩에 의한 스케일 공간
  • $(y,x,t)$로 표현되는 스케일 공간으로, 가우시안 스케일 축이 추가된 3차원 공간이다.
    • 가우시안 $\sigma$는 필터 사이즈와 연관된다.

SIFT 검출

• Scale Invariant Feature Transform: 크기에 불변한 특징 검출
  • 두 이미지를 registration(똑바로 펼침)
• 파노라마 영상을 만들기 위해서는 영상들을 matching 하는 작업이 필요하다.
  • 특징점 매칭: 각각의 영상으로부터 특징점을 검출하고 영상들 간 corresponding pairs를 찾는다.
    • 각 이미지에서 특징에 대한 벡터인 descriptors의 공통점을 찾는다.
    • 이후 Rotation, Scale, Transform 등을 계산해서 영상들을 정렬한다.

Problems when Matching with Features

1. 각 영상으로부터 똑같은 특징점을 찾아야 한다. - 반복성
2. 똑같은 특징점들을 비교하여 매칭해야 한다.
   • 다른 특징과 구분되는 각 특징을 잘 나타내는 기술자가 필요하다.

Difference of Gaussian

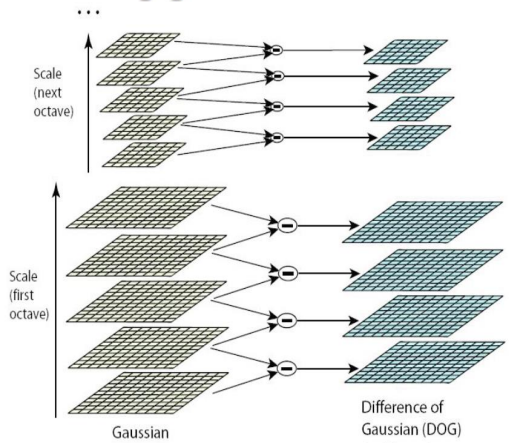
• 각 scale에서 서로 다른 $\sigma$를 적용하고 Gaussian의 차이를 계산해서 local minima 또는 maxima를 찾는다.
  • $t$ 축에서 지역 극점을 탐색한다.
  • 검출된 키포인트가 한단계 큰, 작은 DoG에서는 검출되지 않고 다음 octave(scale)에서도 마찬가지라면 해당점은 특징점으로 적절하다.
• 키포인트는 $(y,x,o,i)$ 정보를 가지는 descriptor이다.
  • 위치와 스케일 계산 식을 거쳐 옥타브별로 검사하는 수식
    • $s=1.6\times2\frac{o+i'}{3}$

정규 라플라시안 맵 구축

필터 형태는 laplacian 필터와 유사하다. DoG는 단지 차영상을 계산하기 때문에 두번 미분하는 정규 라플라시안보다 매우 빠르다.

SURF 검출

• SIFT 검출 알고리즘의 경우 반복적으로 DoG를 계산하기 때문에 시간 소요가 매우 크다.
  • 반복률 희생 없이 DoG 필터를 미리 만들어 더 빠른 계산을 수행하는 SURF 알고리즘이 등장하였다.