Optimization

Linear Classifier의 경우 파라미터에 따른 손실 함수 $L(W)$는 다음과 같이 정의된다.

$L$이 정의되었을 때 $L$을 최소화하는 최적의 파라미터 $W$는 어떻게 구할 수 있을까.

Gradient

직접 $L$을 미분하여 기울기를 계산하는 과정은 연산이 매우 오래 걸리는 문제가 있다. 반면, analytic gradient를 계산하면 정확하고 빠르게 진행할 수 있다.

Gradient Descent

while True:
	weights_grad = evaluate_gradient(loss_fn, data, weights)
    weights += - step_size * weights_grad

현재 $L$ 값을 weight에 대하여 미분하고 계산된 기울기 반대 방향, 즉 손실 값이 작아지는 방향으로 weight가 업데이트 되는 과정이다.
하나의 gradient를 계산하기 위해 모든 데이터를 읽어야 하는 단점이 있다.

Mini-batch Gradient Descent

앞선 단점을 해결하기 위해 학습 데이터의 일부분을 사용하여 weight를 업데이트 하는 방법이다.

while True:
	data_batch = sample_training_data(data, 256)
    weights_grad = evaluate_Gradient(loss_fn, data_batch, weights)
    weights += - step_size * weights_Grad

위의 예시에서 하나의 배치에 포함된 데이터의 개수는 256개이다. Mini-batch의 데이터 $D_B$는 전체 데이터 $D$에서 임의로 샘플링한 집합이다. $D_B$의 분포는 $D$의 분포와 동일하다고 가정하며, 배치의 크기는 클수록 유리하다.

Stochastic Gradient Descent의 문제점

데이터의 개수 $N$이 커질수록 전체 데이터셋에 대한 평균 손실을 계산량 또한 많아진다. SGD는 이 문제를 해결하기 위해 전체 데이터셋을 사용하는 대신 일부 샘플만 사용해서 gradient를 계산하는 방식이다. (Mini-batch Gradient Descent 혼용)
하지만 SGD 방식에는 크게 세 가지 문제가 있다.

1. Loss의 변화율이 방향(차원)마다 다를 때 (Poor Conditioning)
2. Local minima 혹은 saddle point에 빠졌을 때
3. Minibatch가 균일하지 않을 때

Loss의 변화율이 방향마다 다를 때

손실 함수가 한 방향으로는 빠르게 변하고, 다른 방향으로는 완만하게 변하는 경우가 발생할 수 있다.

• 이러한 경우 가파른 축에서는 gradient가 커서 weight가 심하게 흔들리는 jitter 현상이 발생한다.
• 완만한 축에서는 gradient가 작아서 업데이트가 매우 느리다.

Local minima | Saddle point에 빠졌을 때

Saddle point(안장점): 어느 점에서 보면 극댓값이고 다른 곳에서 보면 극솟값인 지점으로, 극값을 가지지 않는 점이다.

Local minima 혹은 Saddle point 지점에서 gradient가 0이 되기 때문에 SGD가 멈추거나 느려질 수 있다. 다시 말해, Zero gradient는 Gradient descent의 stuck을 유발한다. 특히 고차원 공간에서 saddle point가 흔하게 나타난다.

Minibatch noise 문제

SGD는 매 스텝마다 미니배치의 gradient를 계산한다. 따라서 gradient에 noise가 있을 수 있다.
이로 인해 weight 업데이트 경로가 불안정하고 진동하거나 최적점 근처에서 정확한 수렴이 어려울 수 있다.

Momentum 기법

Momentum 기법은 기존 SGD의 문제점을 완화하기 위한 방법이다. Momentum은 관성을 이용해 앞서 본 세 가지 문제를 완화한다. 기본 SGD에서 weight가 업데이트될 때 느리고 흔들림이 많은 반면, momentum은 이에 비해 매끄럽고 빠르게 최적점에 수렴한다.

SGD + Momentum

과거 gradients의 누적 평균을 사용하여 부드럽게 업데이트한다.

# 기본 SGD
while True:
	dx = compute_gradient(x)
    x -= learning_rate * dx

# SGD + Momentum
vx = 0
while True:
	dx = compute_gradient(x)
    vs = rho * vs + dx
    x -= learning_rate * vx

• Velocity vx는 gradients의 평균을 의미한다.
• 이전 값을 얼마나 반영할지 결정하는 rho는 관성 계수로, 보통 0.9~0.99 사이의 값을 사용한다.

Nesterov Momentum

Momentum 기법은 현재 위치의 gradient를 이용하지만, Nesterov Momentum은 예측된 미래 위치에서의 gradient를 사용한다.

• $v_{t+1}=\rho v_t-\alpha\nabla f(x_t+\rho v_t)$
• $x_{t+1}=x_T+v_{t+1}$

먼저 다음 step에 가본 후 gradient를 측정하기 때문에 방향이 더 정확하고, 빠르게 수렴할 수 있다.

AdaGrad

AdaGrad 기법은 각 weight마다 학습률을 자동으로 조절하는 기법이다. 많이 변화하는 파라미터는 학습률을 줄이고, 덜 변화하는 파라미터는 학습률을 유지한다. Gradient의 크기는 다음과 같이 계산된다.

• Weight는 기존 SGD 방법에, gradient 각 원소별 scaling 연산을 거쳐 업데이트 된다.
  • $\theta_{t+1}=\theta_t-\frac{\eta}{\sqrt{G_t+\epsilon}}$
  • 이 과정을 거쳐 크기가 큰 gradient를 줄일 수 있다.

그동안의 gradient 크기에 따라 업데이트 크기를 조절함으로써, 자주 변화하는 방향은 작게, 덜 변화하는 방향은 크게 업데이트하여 방향마다 다른 속도로 수렴하게 된다.

하지만 $G_t$는 gradient의 크기를 누적한 값이기 때문에 매 반복마다 증가한다. 이로 인해 learning rate가 대폭 감소하게 된다. 학습률이 점점 0에 가까워지면 학습이 일찍 멈추는 현상이 발생할 수 있다.

RMSProp: Leaky AdaGrad

AdaGrad 방식의 문제점을 해결하기 위해 gradient의 누적합을 완전히 유지하지 않고, 적당히 잊어버리는 방식으로 조절하는 것이 Leaky AdaGrad 방식이다. 파라미터 $\theta$의 업데이트 방식은 동일하지만 $G$의 업데이트 방식은 다음과 같다.

오래된 gradient의 영향력을 $\gamma$로 조절하여 $G$가 너무 커지지 않게 하는 방식이다. 이를 통해 학습률이 급격이 줄어는 현상을 방지할 수 있다.

Adam

Adam (Adaptive Moment Estimation)은 Momentum 기법과 Adaptive Gradient 기법의 결합이다. 최근 gradients의 평균인 momentum과 최근 gradients의 제곱의 평균을 조합해서 각 파라미터마다 다르게 조절된 학습률을 적용한다.

AdamW

Adam은 정규화 항까지 포함해서 gradient를 처리한다. 이로 인해 gradient scale에 의해 정규화 효과가 왜곡되고, weight decay가 제대로 작동하지 않는다. 이 문제를 해결하기 위해 등장한 것이 AdamW이다.

• Weight decay 항은 gradient에 포함하지 않고, 매 step마다 직접 파라미터에 따로 적용한다.

Learning Rate Schedules

Learning rate는 하이퍼파라미터로, 최적점에 도달하기 위해 적절한 learning rate를 찾아야 한다. 아래 그래프처럼 learning rate에 따라 loss의 변화는 매우 다양해진다.

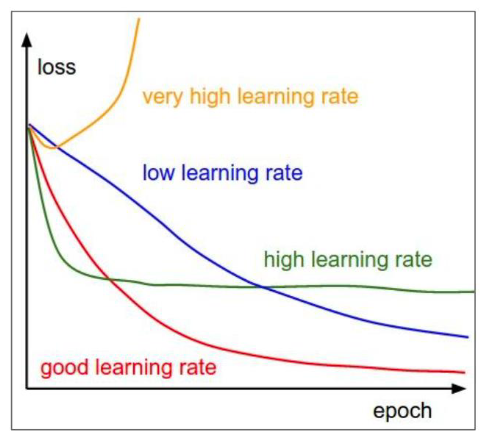
참고로, 위 그래프에서 low learning rate는 최솟값에 도달하는 것처럼 보이지만 local minimum에 빠질 수 있다.

적절한 learning rate를 찾기 위해 다양한 learning rate scheduling 전략이 있다.

1. 학습 도중 학습률을 점차 감소시키는 방식 (Step, Cosine, Linear, Inverse square root)
2. 초반에 학습률을 천천히 키워주는 방식

Step Decay

정해진 시점에 학습률을 급격히 줄인다.
예) 30, 60, 90 epoch마다 LR을 0.1배로 감소시킨다.

Cosine Decay

학습률을 코사인 형태로 부드럽게 줄여나간다.

• $\alpha_0$: 초기 LR
• $\alpha_t$ $t$ 시점에서 LR
• $T$: 전체 반복 횟수 (epoch)

Linear Decay

학습률을 직선적으로 감소시킨다.

Inverse Square Root Decay

Epoch 수의 제곱근에 반비례하여 학습률을 줄인다.

이 경우 초기에는 빠르게 감소하다가 점점 느리게 감소한다. (굴 생존곡선 형태)

Linear Warmup

학습 초기에 너무 큰 학습률을 사용하면 loss가 폭발할 수 있다. 이를 막기 위해 초반 학습에는 학습률을 천천히 키워주는 전략이 필요하다. 보통 초기 5000 반복 동안 학습률을 0에서 선형적으로 증가시키고, 이후 decay 스케줄에 따라 감소시킨다.

• Batch size를 $N$만큼 늘리면 초기 학습률도 $N$배, $\sqrt{N}$배 늘리는 것이 일반적이다.