[CS]탐욕법(Greedy)

Greedy : 탐욕법

• 현재 + 최적이라 생각되는 것을 선택해나가는 방식
• 지역해에 빠질 수 있음 => 최적해 보장 X
  

Greedy 적용 조건

• Greedy는 두 조건이 성립된 문제에 한해 적용 가능

1. 탐욕 선택 속성(Greedy Choice Property)
   -지역해 = 최적해인 경우 적용 가능
2. 최적 부분 구조(Optimal Substructure)
   -부분 최적 해들의 총합 = 전체 최적 해

Greedy 구현 방법

1. 선택 절차(Selection Procedure)
   -’현재 상태’에서 최적의 선택을 수행
2. 적절성 검사(Feasibility Check)
   -선택된 항목이 ‘문제의 조건’을 만족하는지 확인
3. 해답 검사(Solution Check)
   -모든 선택 완료 시, ‘최종 선택’이 ‘문제의 조건을 만족’하는지 확인

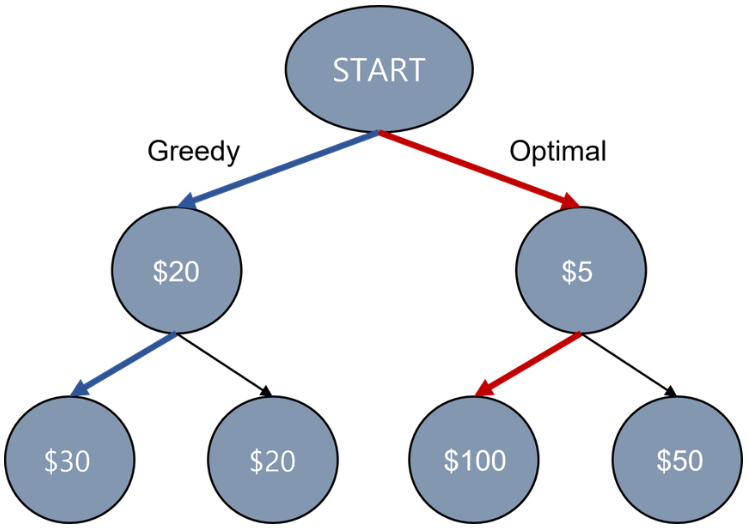
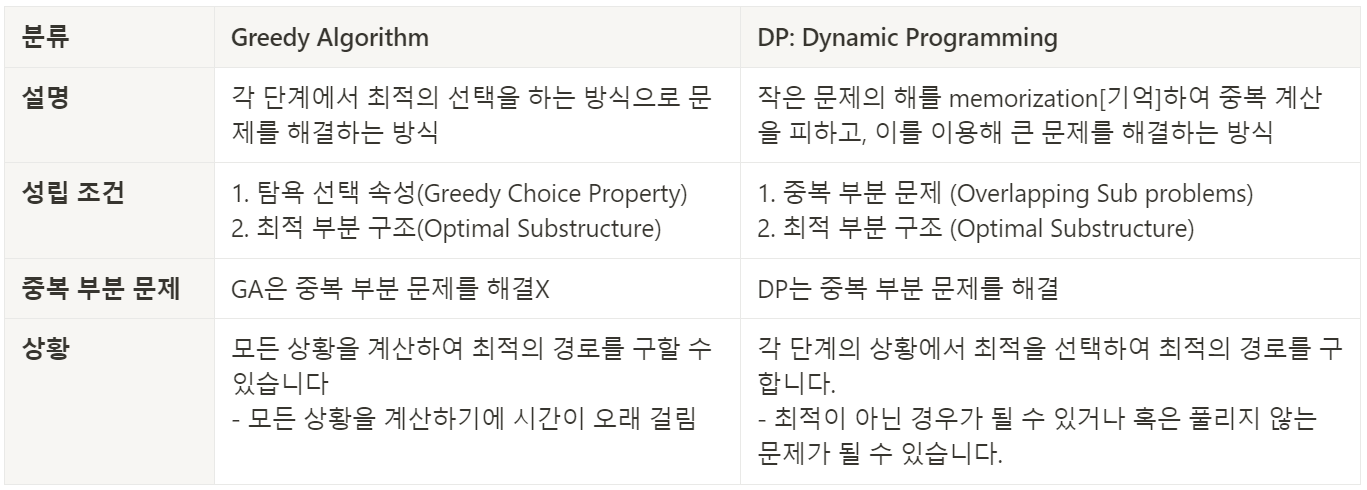
Greedy VS DP

Greedy 예제

1. 거스름돈 문제

• 카운터에는 거스름돈으로 사용할 500원, 100원, 50원, 10원짜리 동전이 무한히 존재
• 거슬러줄 돈이 N원일 때 거슬러 줘야할 동전의 최소 개수를 구하라. (단, N은 항상 10의 배수)
• 아이디어 두 가지
  • 최소 동전의 개수이므로 큰 동전(500원)부터 거슬러준다.
  • 거슬러 준 만큼 N에서 뺀다.
  • 몫의 계산으로 동일하게 접근했지만, 단순히 N에서 빼는 것이 아니라 나머지를 계산해주면 더 간단

N=1260
cnt=0
for i in [500,100,50,10]:
    num_ = N//i
    N=N-num_*i
    cnt+=num_
print(cnt)

N=1260
cnt=0
for i in [500,100,50,10]:
    cnt += N//i
    N%=i
print(cnt)