1. 비트 마스킹 : Bit Masking
- Bit + Masking
- Bit : 프로그램 데이터의 최소 단위
- Masking : 색칠하는 것 / 1 or 0
- 컴퓨터는 내부적으로 모든 자료를 이진수로 표현
- 비트 마스크 : 정수의 이진수 표현을 자료구조로 쓰는 기법
- 장점
- 더 빠른 수행시간
- 더 간결한 코드
- 더 적은 메모리 사용
2. 비트 연산
2-1. a & b : a AND b
- 동일한 bit 자리수 AND 연산
- 둘다 1일 경우 1
- 그 외 0
- 예시
- a = 4 = 1002
- b = 7 = 1112
- a & b = 1002 = 4
2-2. a | b : a OR b
- 동일한 bit 자리수 OR 연산
- 둘다 0일 경우 0
- 그 외 1
- 예시
- a = 4 = 1002
- b = 7 = 1112
- a | b = 1112 = 7
2-3. a ^ b : a XOR b
- 동일한 bit 자리수 XOR 연산
- 둘이 다를 경우 1
- 둘이 같다면 0
- 예시
- a = 4 = 1002
- b = 6 = 1102
- a | b = 0102 = 2
2-4. ~a : NOT a
- bit 자리수 부정(반전) 연산
- 비트의 값을 Toggle
- 0 -> 1
- 1 -> 0
- 예시
- a = 4 = 1002
- ~a = 0112 = 3
2-5. a << b
- shift 연산자
- a를 b만큼 왼쪽으로 shift
- [TIPS] 2의 제곱을 표현하는 표현으로 사용
- 예시
- a = 1 = 0012
- a << 2 = 1002 = 4
5. a >> b
- shift 연산자
- a를 b만큼 오른쪽으로 shift
- [TIPS] 2의 정수 나누기(나머지 버림)을 표현하는 표현으로 사용
- 예시
- a = 4 = 1002
- a >> 2 = 0012 = 1
3. 비트 마스킹 응용 : 집합
- 비트 마스킹은 집합을 쉽게 표현 가능
- 각 원소마다 비트를 하나씩 대응시킴
- 집합의 원소 추가 / 삭제 등 다양한 연산 또한 쉽게 표현 가능
- ex {A, B, C, D, E, F, G}
- {A} = 64 = 10000002
- {C, F} = 18 = 00100102
3-1. 원소 추가
- 현재 상태(cur)에서 p번 원소 추가
- cur에서 p번 원소를 1로 변화
- 나머지 비트는 상태 유지
cur = cur | (1 << p);
3-2. 원소 삭제
- 현재 상태(cur)에서 p번 원소 삭제
- cur에서 p번 원소를 0으로 변화
- 나머지 비트는 상태 유지
cur = cur & ~(1 << p);
3-3. 원소 토글
- 현재 상태(cur)에서 p번 원소 토글(toggle)
- cur에서 p번 원소를 ~cur으로 변화
- 나머지 비트는 상태 유지
cur = cur ^ (1 << p);
4. 집합 연산
- 비트 마스킹을 이용해 집합 연산을 쉽게 수행 가능
- 집합 연산
a | b
a & b
a & ~b
a ^ b
5. 집합 크기
- 1인 비트(원소)의 수를 카운트
- x % 2를 통해 마지막 bit 획득
- x / 2를 통해 마지막 bit 삭제
- 모든 비트를 재귀적으로 순회
int bitCount(int x){
if(x == 0) return 0;
return x % 2 + bitCount(x / 2);
}
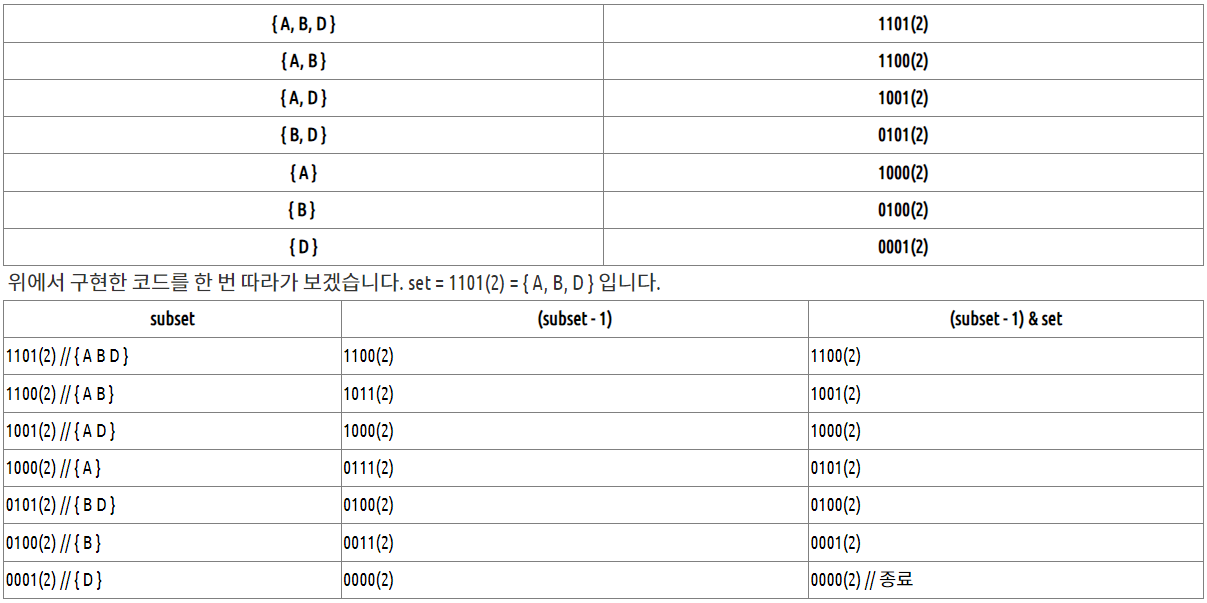
6. 집합 순회
for(int subset = set; subset; subset = (subset - 1) & set){
}
- 집합 {A, B, D}의 모든 부분 집합(에 대응하는 정수)을 순회한다.