[CS]이분 탐색(Binary Search)

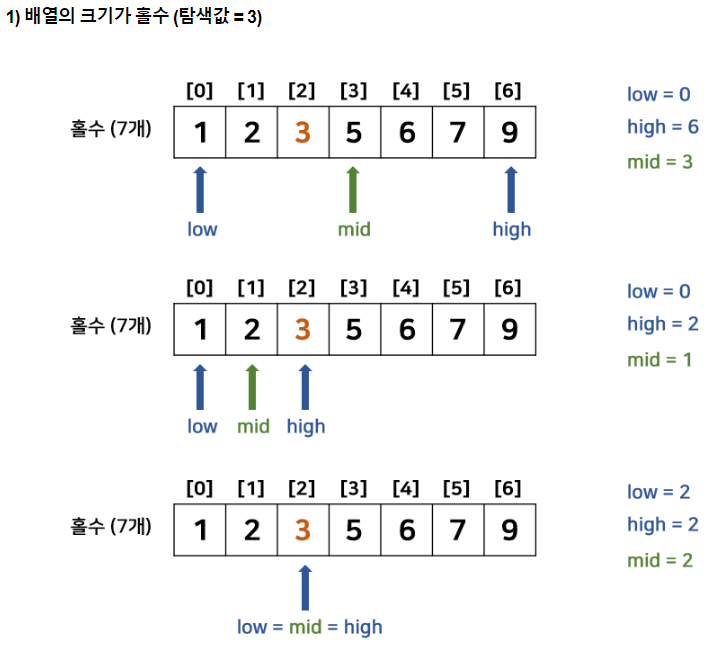
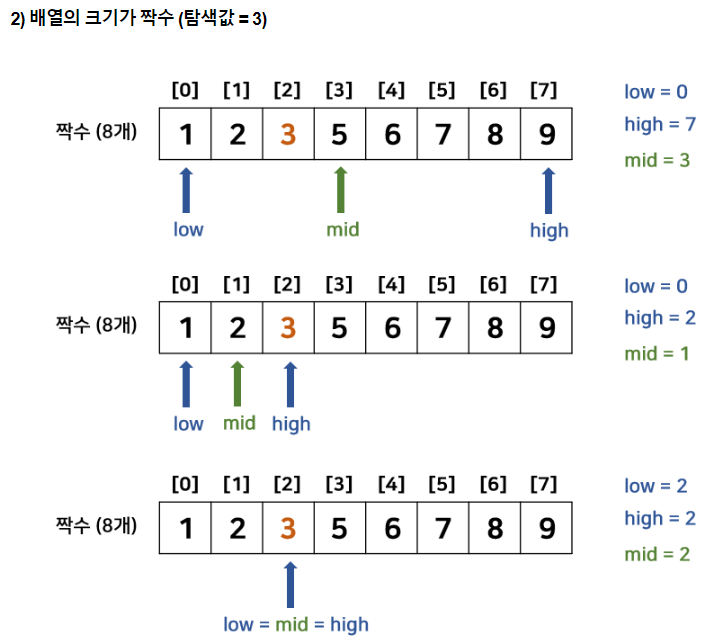
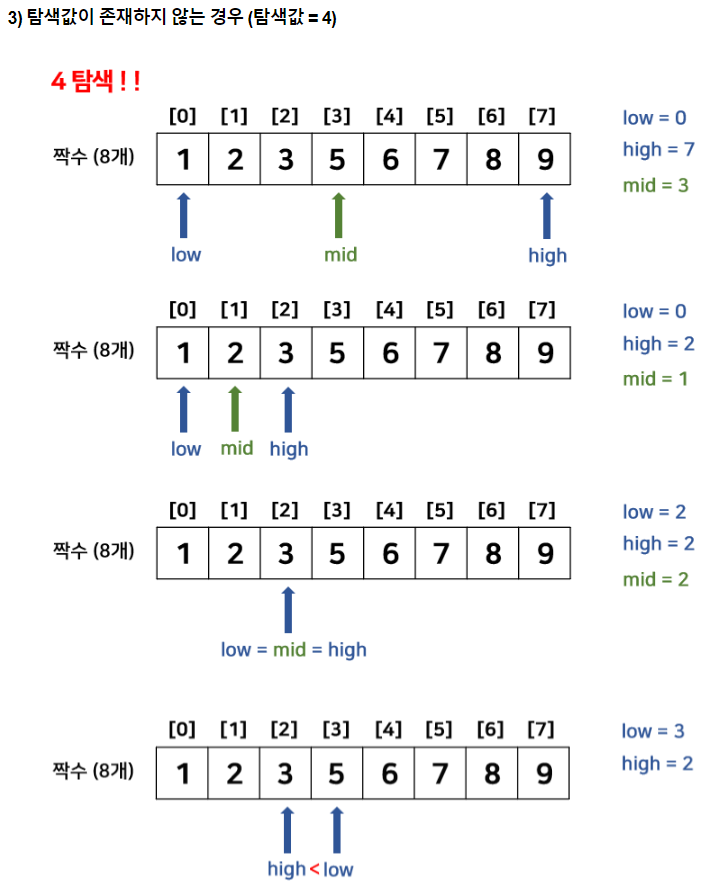
이분 탐색 : Binary Search

• 이분 탐색이라 말하면 못알아먹는데 Binary Search라 말하면 알아먹는다.
• [IMP] 정렬된 배열에만 사용 가능한 탐색기법
• 중앙 값을 기반으로 불필요한 탐색범위를 줄여가는 기법
• 알고리즘
  
  
  • low <= high라면 아래 과정 반복
    • low = 현재 탐색 배열의 시작 점
    • high = 현재 탐색 배열의 끝 점
    • middle = (low + high) / 2
    • 탐색 값 > middle
      • low - middle - 1 범위에서 재탐색(재귀 호출)
    • 탐색 값 = middle
      • 탐색 완료
    • 탐색 값 < middle
      • middle + 1 - high 범위에서 재탐색(재귀 호출)
  • low > high라면 탐색 값 존재 X
    
• 시간 복잡도 : $O(log_2n)$

Binary Search 코드

int binary_search(vector<int>& v, int num){
	int low = 0;//시작점
    int high = v.size() - 1;//끝넘
    int idx = -1;//반환 값
    while(low <= high){
    	int mid = (low + high) / 2;
        //1. 탐색 값을 찾으면 멈춤
        //2. 탐색 값 < 중앙 값 -> 끝점 갱신
        //3. 탐색 값 > 중앙 값 -> 시작점 갱신
        if(v[mid] == num){
        	idx = mid;
            break;
        }
        else if(num < v[mid]) high = mid - 1;
        else if(v[mid] < num) low = mid + 1;
    }
    return idx;
}

C++ STL Binary Search

lower_bound / upper_bound

• C++에선 이진탐색(binary search)에 대한 라이브러리 함수 lower_bound & upper_bound를 제공한다.
• lower_bound(iter start, iter end, T val)
  • [start - end) 범위에서 val보다 크거나 같은 iter를 반환
• upper_bound(iter start, iter end, T val)
  • [start - end) 범위에서 val보다 큰 iter를 반환

vector<int> vec = {1,2,2,2,2,2,8,9};
cout << lower_bound(vec.begin(), vec.end(), 2) - vec.begin() << '\n'; // 1
cout << upper_bound(vec.begin(), vec.end(), 2) - vec.begin() << '\n'; // 6