시간 복잡도
특정한 크기의 입력에 대하여 알고리즘이 얼마나 오래 걸리는지에 관련된 것이 바로 '시간 복잡도'이다. 입력값과 연산 수행 시간의 상관관계를 나타내는 척도를 말하며, 보통 빅오표기법을 사용한다.
효율적인 알고리즘을 구현한다는 것은 바꾸어말해 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화한 알고리즘을 구성했다는 이야기다.
<시간복잡도 표현 방법>
- 최상의 경우 : 오메가 표기법 (하한 점근)
- 평균의 경우 : 세타 표기법
- 최악의 경우 : 빅오 표기법 (상한 점근)
평균을 생각해 세타 표기법을 사용한다고 생각할 수 있으나 평가하기 까다로워 보통 최악을 기준으로 빅오 표기법으로 판단해 성능을 예측한다.
"이 정도까지도 걸릴 수 있다"라는 경우를 고려해야 그에 맞는 대응이 가능하기 때문이다.
빅오표기법
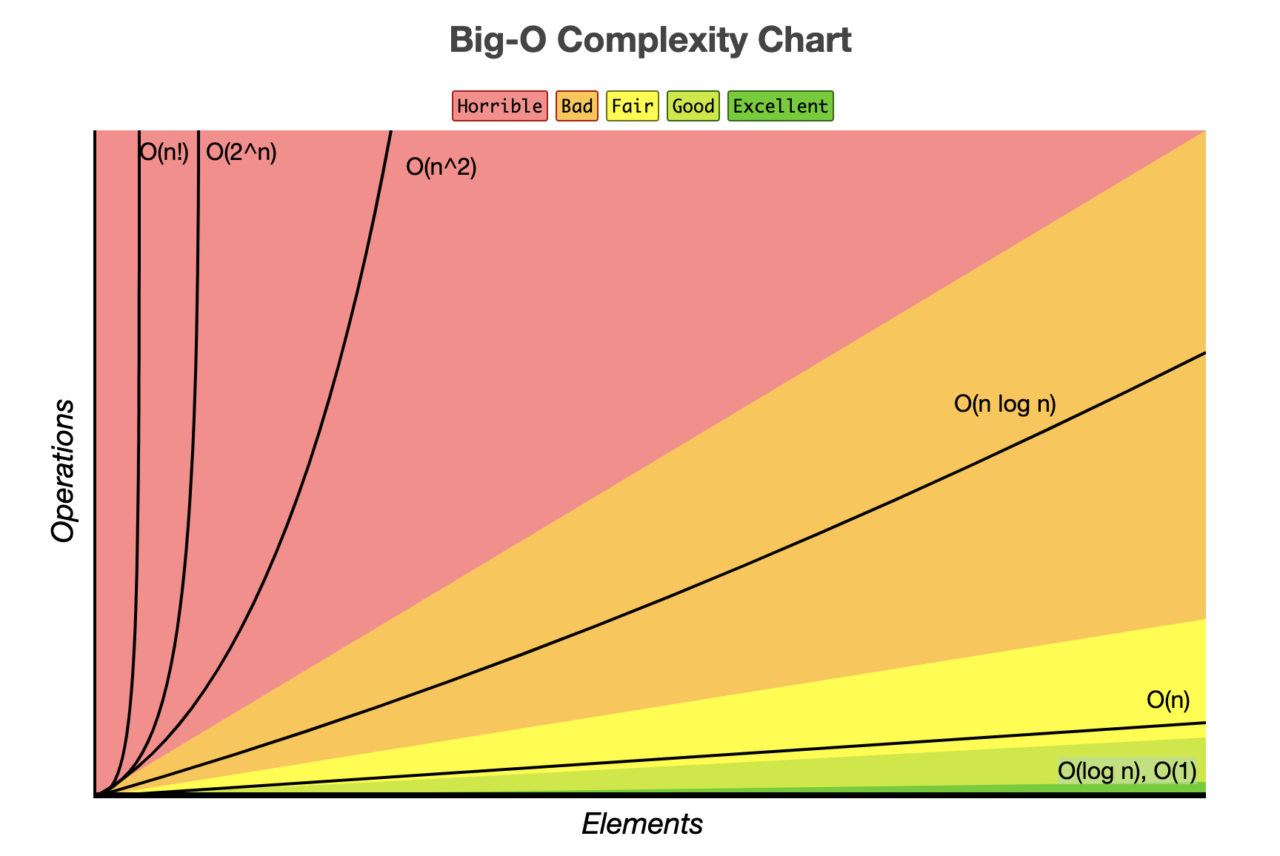
알고리즘을 수행하기 위해 프로세스가 수행해야 하는 연산을 수치화한 것이다. 실행시간은 커뮾터의 하드웨어 또는 프로그래밍 언어에 따라 편차가 달라지기 때문에 명령어의 연산 횟수를 기준으로 나타낸다.
O(1)
일정한 복잡도라고 하며, 입력값이 증가하더라도 시간이 늘어나지 않는다.
O(n)
선형 복잡도라고 하며, 입력값이 증가함에 따라 시간 또한 같은 비율로 증가하는 것을 의미한다.
일반적으로 1중 반복문의 경우가 이에 해당한다.
O(log n)
로그 복잡도라고 부르며, O(1) 다음으로 빠른 시간 복잡도를 가진다. 이진 탐색 트리가 해당 시간 복잡도에 해당한다.
O(n^2)
2차 복잡도라고 부르며, 입력값이 증가함에 따라 시간이 n의 제곱수의 비율로 증가하는 것을 의미한다.
일반적으로 2중 반복문의 경우가 이에 해당한다. (3중, 4중, 5중으로 사용해도 보통 O(n^2)으로 표기한다.)
O(n log n)
선형 로그 복잡도라고 부르며, 대체로 입력의 절반(또는 일부)으로 나눌때마다 각 부분을 독립적으로 처리하는 알고리즘(병합정렬, 퀵정렬, 힙정렬 등)이 이에 해당한다.
O(2^n)
입력값이 증가함에 따라 시간이 2의 n제곱수의 비율로 증가하는 것을 의미한다. 재귀로 표현하는 피보나치 수열이 이에 해당한다.
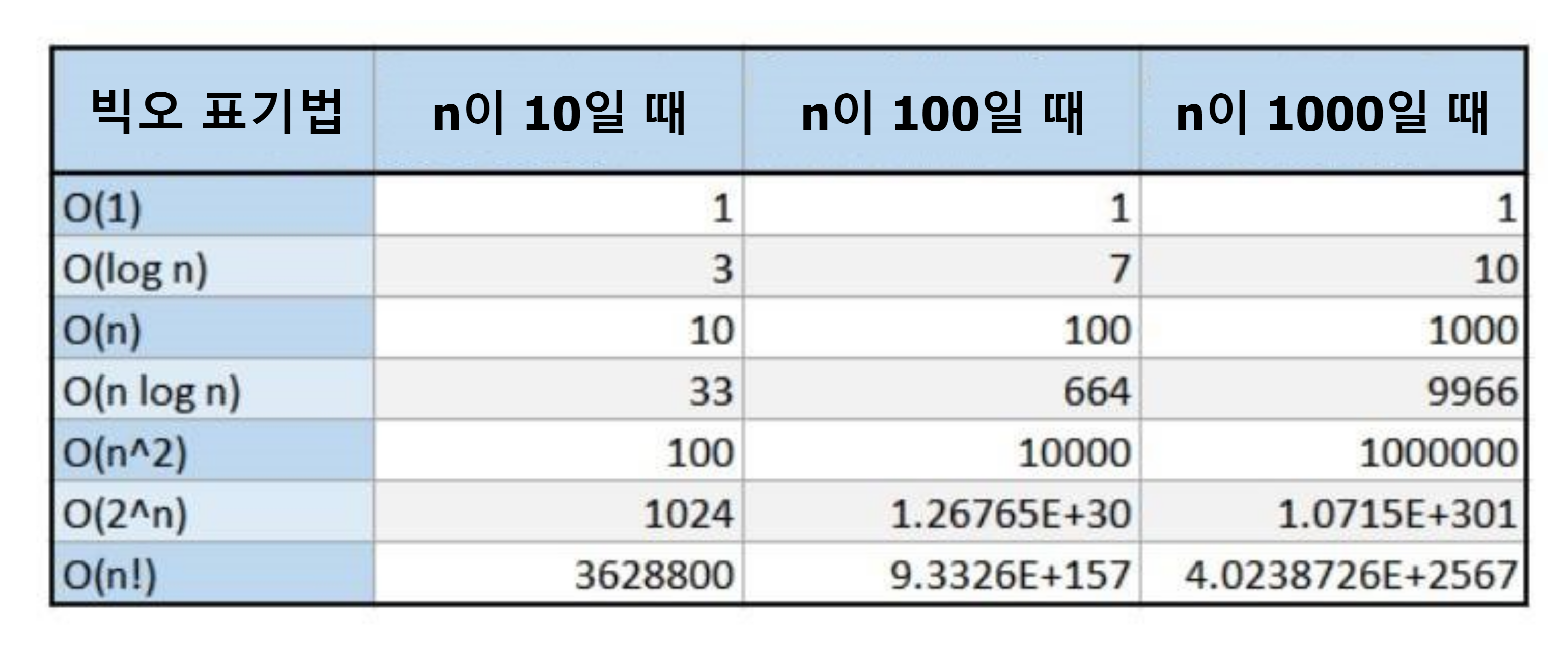
공간 복잡도
특정한 크기의 입력에 대하여 알고리즘이 얼마나 많은 메모리를 차지하는지에 관련된 것이 공간 복잡도이다. 프로그램을 실행시켰을 때 필요로 하는 자원 공간의 양을 말한다.
자료구조에서의 시간복잡도
자료구조란?
대량의 데이터를 효율적으로 관리할 수 있는 데이터의 구조를 의미한다. 데이터에 편리하게 접근, 변경하기 위해 데이터를 저장하거나 조직하는 방법을 말한다.
자주 쓰는 자료구조의 평균, 최악 시간 복잡도
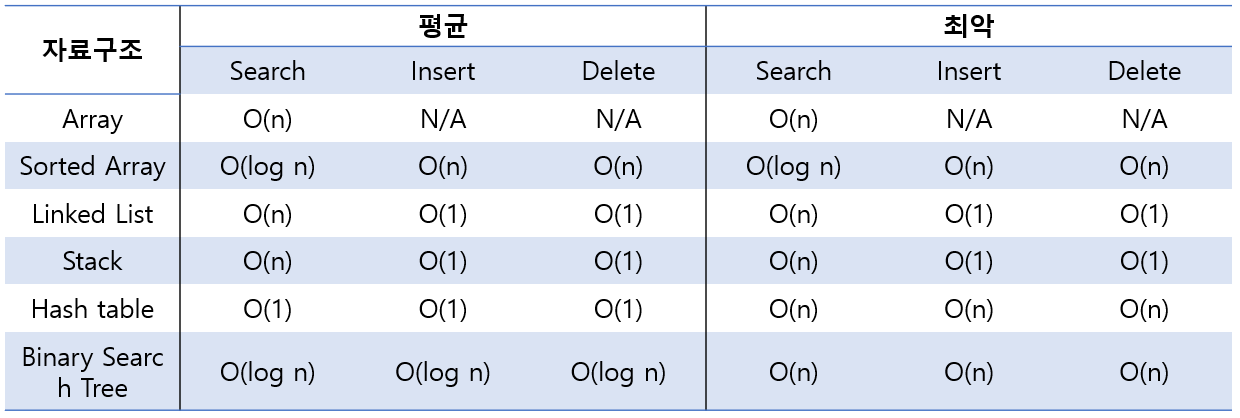
참고
https://junghyun100.github.io/Time-Complexity/
https://chancoding.tistory.com/43
https://velog.io/@yarogono/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EC%8B%9C%EA%B0%84-%EB%B3%B5%EC%9E%A1%EB%8F%84-%EC%A0%9C%EB%8C%80%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EC%9E%90
https://hanamon.kr/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-time-complexity-%EC%8B%9C%EA%B0%84-%EB%B3%B5%EC%9E%A1%EB%8F%84/
https://joyhong-91.tistory.com/12
https://bangu4.tistory.com/202
https://cordcat.tistory.com/75
https://jocoma.tistory.com/entry/%EC%8B%9C%EA%B0%84-%EB%B3%B5%EC%9E%A1%EB%8F%84-%EA%B3%B5%EA%B0%84-%EB%B3%B5%EC%9E%A1%EB%8F%84
https://velog.io/@ghldjfldj/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0%EB%9E%80
