그래프
여러 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조로, 정점간의 관계를 표현한 조직도이다. 두 정점 사이를 이어주는 간선과 정점으로 이루어진다.
즉, 정점과 그 정점을 연결하는 간선을 하나로 모아 놓은 자료 구조다.
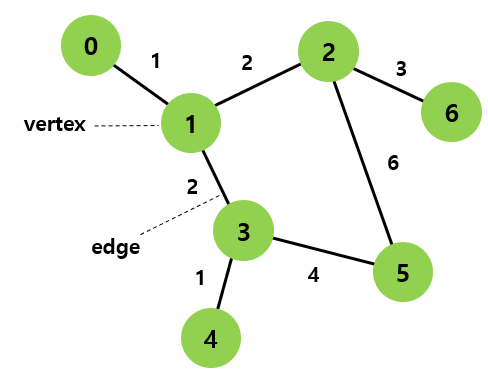
- 정점 : 데이터가 저장되는 그래프의 기본 원소
- 간선 : 정점 간의 관계를 나타내는 선
방향 그래프 VS 무방향 그래프
방향 그래프
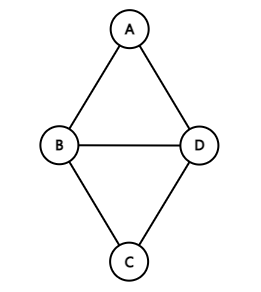
두 정점을 연결하는 간선에 방향이 없는 그래프이다.
무방향 그래프
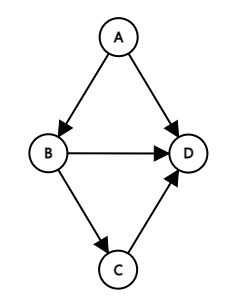
두 정점을 연결하는 간선에 방향이 있는 그래프이다.
가중치 그래프
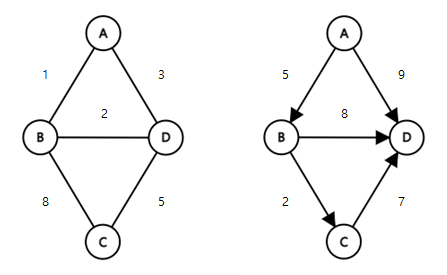
간선에 비용이나 가중치가 할당된 그래프이다.
연결 그래프 VS 비연결 그래프
연결 그래프
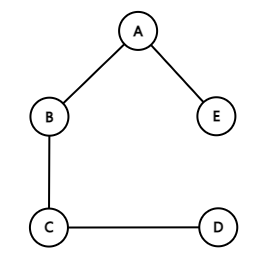
그래프에서 모든 노드가 최소한 하나의 경로로 연결된 그래프이다.
비연결 그래프

그래프에서 일부 노드가 다른 노드와 연결되지 않은 그래프이다.
순환 그래프 VS 비순환 그래프
순환 그래프
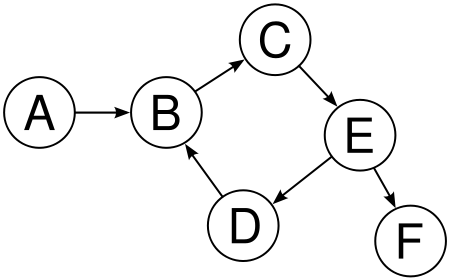
그래프에 사이클이 존재하는 그래프로 한 노드에서 시작하여 다시 해당 노드로 돌아올 수 있는 경로(사이클)이 있는 그래프이다. 적어도 한 개 노드에서 시작하여 다른 노드들을 거쳐 다시 자기 자신으로 돌아오는 경로를 가지는 그래프이다.
비순환 그래프

그래프에 사이클이 존재하지 않는 그래프로 한 노드에서 시작하여 해당 노드로 돌아오는 경로가 없는 그래프이다. 어떠한 경로도 자기 자신으로 돌아오지 않는 순환이 없는 그래프이다.
트리
그래프의 일종으로 방향성이 있는 연결된 비순환 그래프이다. 하지만 일반 그래프와는 달리, 계층 구조를 가진다는 특수성이 있다.
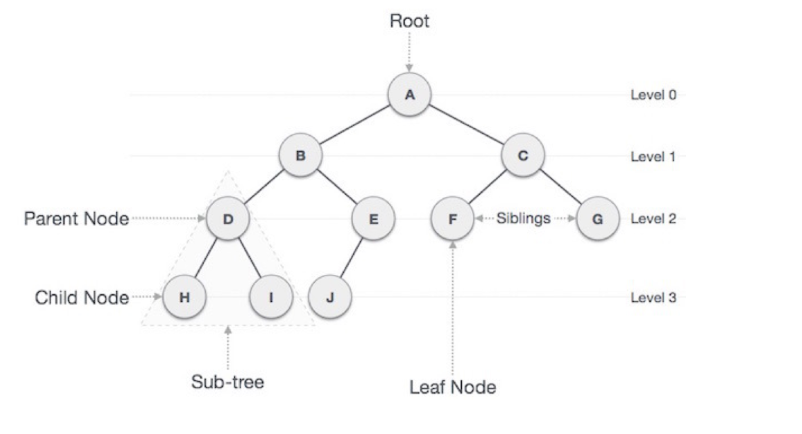
트리의 특징
- 트리는 사이클이 없는 비순환 구조이다.
- 한 정점에서 출발하여 다시 자기 자신으로 돌아오는 경로가 존재하지 않는다.
- 하나의 루트 노드와 0개 이상의 하위 트리를 가진다.
- 루트 노드는 반드시 하나여야 하며, 두 개가 될 수 없다.
- 모든 노드는 단 하나의 부모 노드를 가진다.
- 루트 노드를 제외한 모든 노드는 반드시 하나의 부모 노드를 가져야 한다.
- 노드는 N개인 트리는 항상 N-1개의 간선을 가진다.
- 간선은 항상 정점의 개수 - 1 만큼을 가진다.
- 모든 노드로 갈 수 있는 경로는 루트 노드를 거쳐야만 가능하다.
- 다른 노드들이 모든 경로를 지나기 위해서는 반드시 루트 노드를 거치는 구조를 가진다.
이진트리
자식 노드의 개수가 두 개 이하인 트리를 말한다.
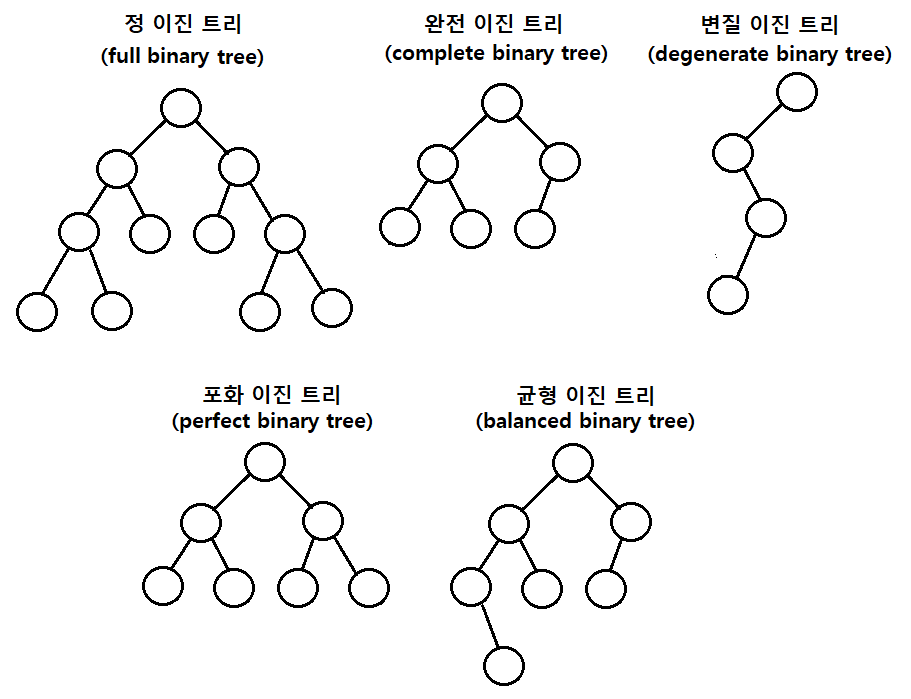
- 정 이진 트리 : 자식 노드가 0 또는 2개인 이진 트리
- 완전 이진 트리 : 왼쪽에서부터 채워져 있는 이진 트리로 마지막 레벨을 제외하고는 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 경우 왼쪽부터 채워져 있는 트리
- 변질 이진 트리 : 자신 노드가 하나밖에 있는 이진 트리
- 포화 이진 트리 : 모든 노드가 꽉 차 있는 이진 트리로 반드시 노드의 개수가 2^(h + 1) - 1의 개수를 가짐
- 균형 이진 트리 : 왼쪽과 오른쪽 노드의 높이 차이가 1 이하인 이진 트리
이진탐색트리
탐색을 위한 이진 트리의 일종으로 특수한 노드 값을 가지는 형태의 이진 트리를 말한다.
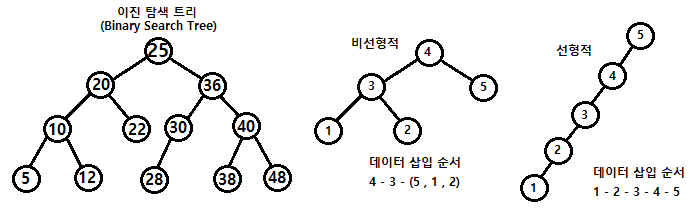
왼쪽 노드에는 부모 노드보다 작은 값이 저장되고 오른쪽 노드에는 부모 노드보다 큰 값이 저장된다. 또한 모든 노드는 중복된 값을 가지지 않는다.
비선형적인 구조로 잘 만들어진 이진탐색트리는 O(log n)의 시간 복잡도를 가지지만 데이터 삽입 순서에 따라 선형적인 구조를 가지게 된 경우에는 최악의 경우 O(n)의 시간복잡도를 가지게 될 수도 있다.
AVL 트리
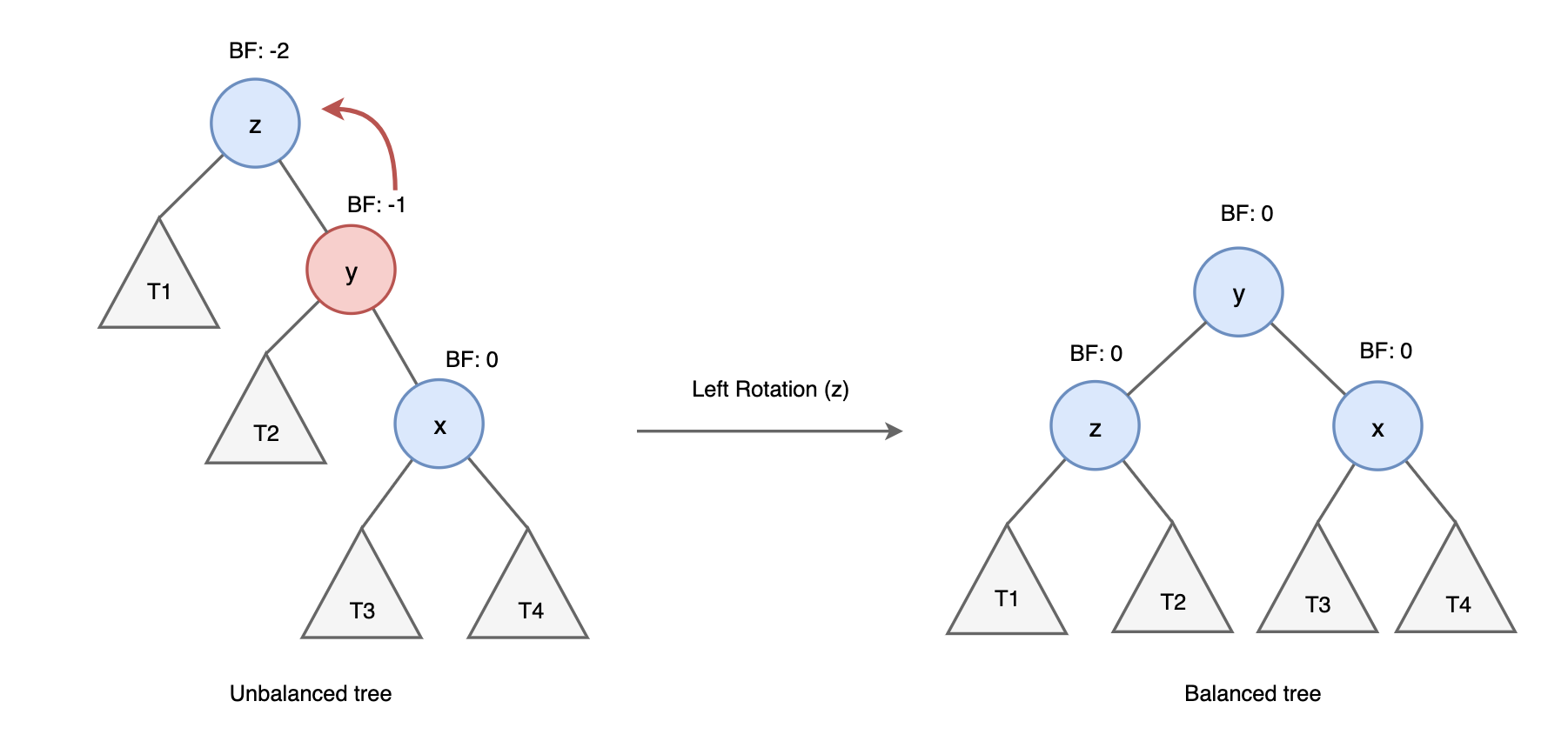
균형 이진 트리의 일종으로 이진 탐색 트리에 균형 트리의 특징을 넣은 트리를 말한다.
이진 탐색 트리와 같은 특징을 가지고 있지만, ACL 트리는 균형 트리의 특징을 가져 서브 트리의 좌, 우 높이 차이가 1을 초과하지 않도록 동작한다.
AVL 트리는 항상 균형을 맞춰 높이를 유지하기 때문에 평균, 최악의 경우 모두 시간 복잡도를 O(log n)을 가지게 된다.
레드블랙트리
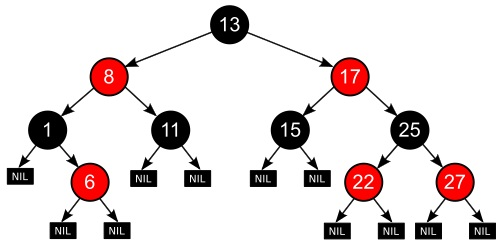
자가 균형 이진 탐색 트리이다. 레드블랙트리는 트리의 모양이 군형 잡히도록 각 노드들은 Red 혹은 Black의 색상을 가지고 모든 경우에서 O(log n)의 시간 복잡도를 보장받는다.
그래프 VS 트리

트라이
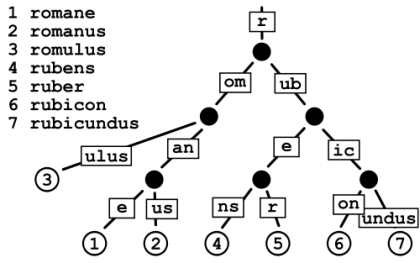
n차 트리의 변종으로 각 노드에 문자를 저장하는 자료구조이다. 따라서 트리를 아래쪽으로 순회하면 단어 하나가 나온다. 접두사를 빠르게 찾아보기 위한 흔한 방식으로, 유효한 단어 집합을 이용하는 많은 문제들은 트라이를 통해 최적화할 수 있다.
힙
완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조이다. 여러 개의 값들 중에서 최대값이나 최소값을 빠르게 찾아내도록 만들어진 자료구조이다. 힙은 반정렬 상태(느슨한 정렬 상태)를 유지한다. 또, 중복을 허용한다는 특징이 있다.
힙의 종류
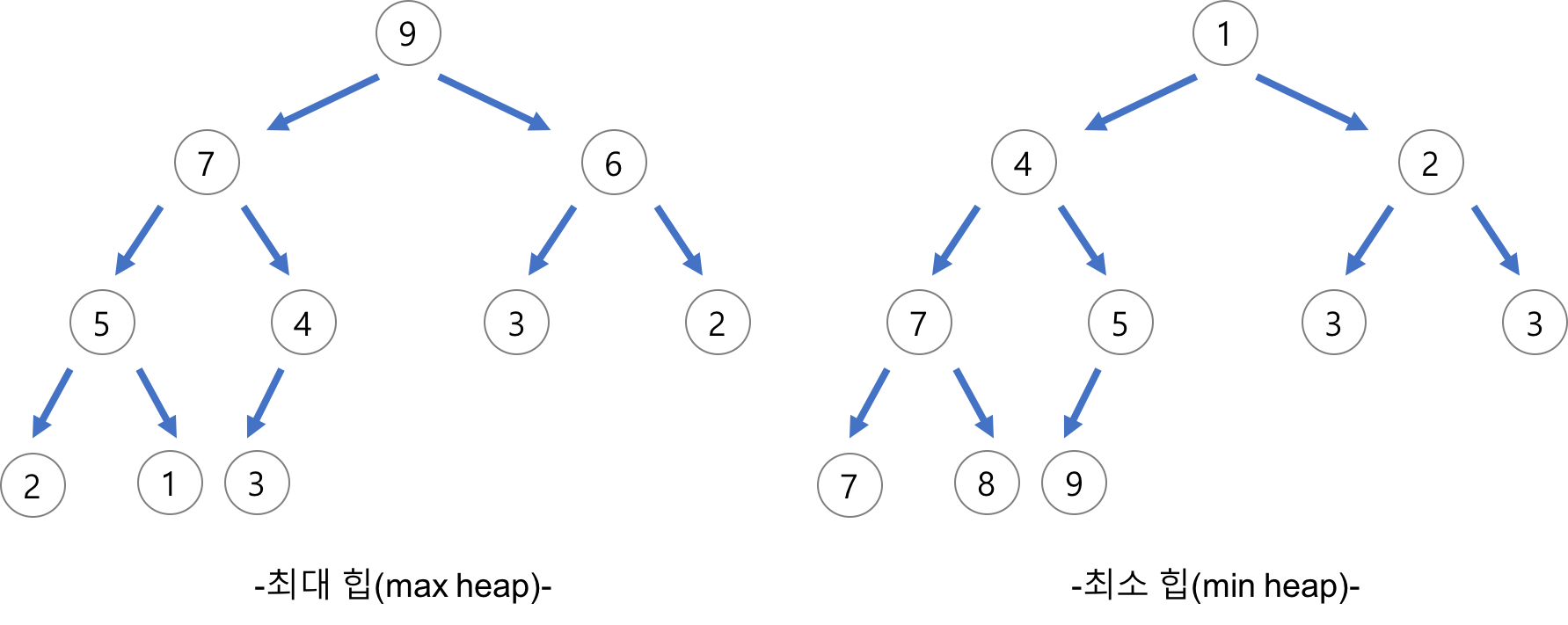
최대힙은 자식 노드보다 부모 노드의 값이 크고, 최소힙은 자식 노드보다 부모 노드의 값이 작다.
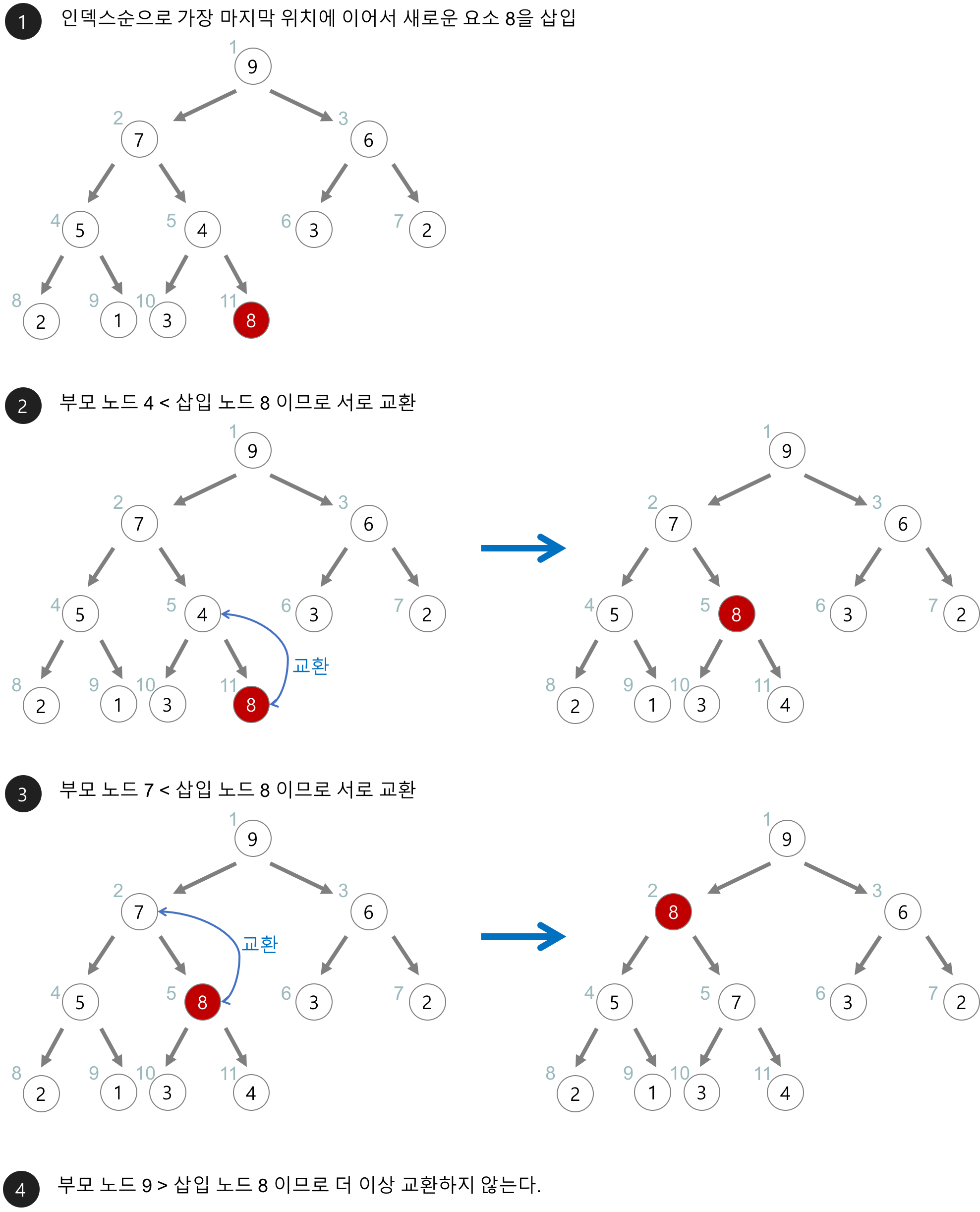
힙 삽입
새로운 요소가 들어오면 일단 새로운 노드를 힙의 마지막 노드에 이어서 삽입한다. 새로운 노드를 부모 노드들과 교환해서 힙의 성질을 만족시킨다.
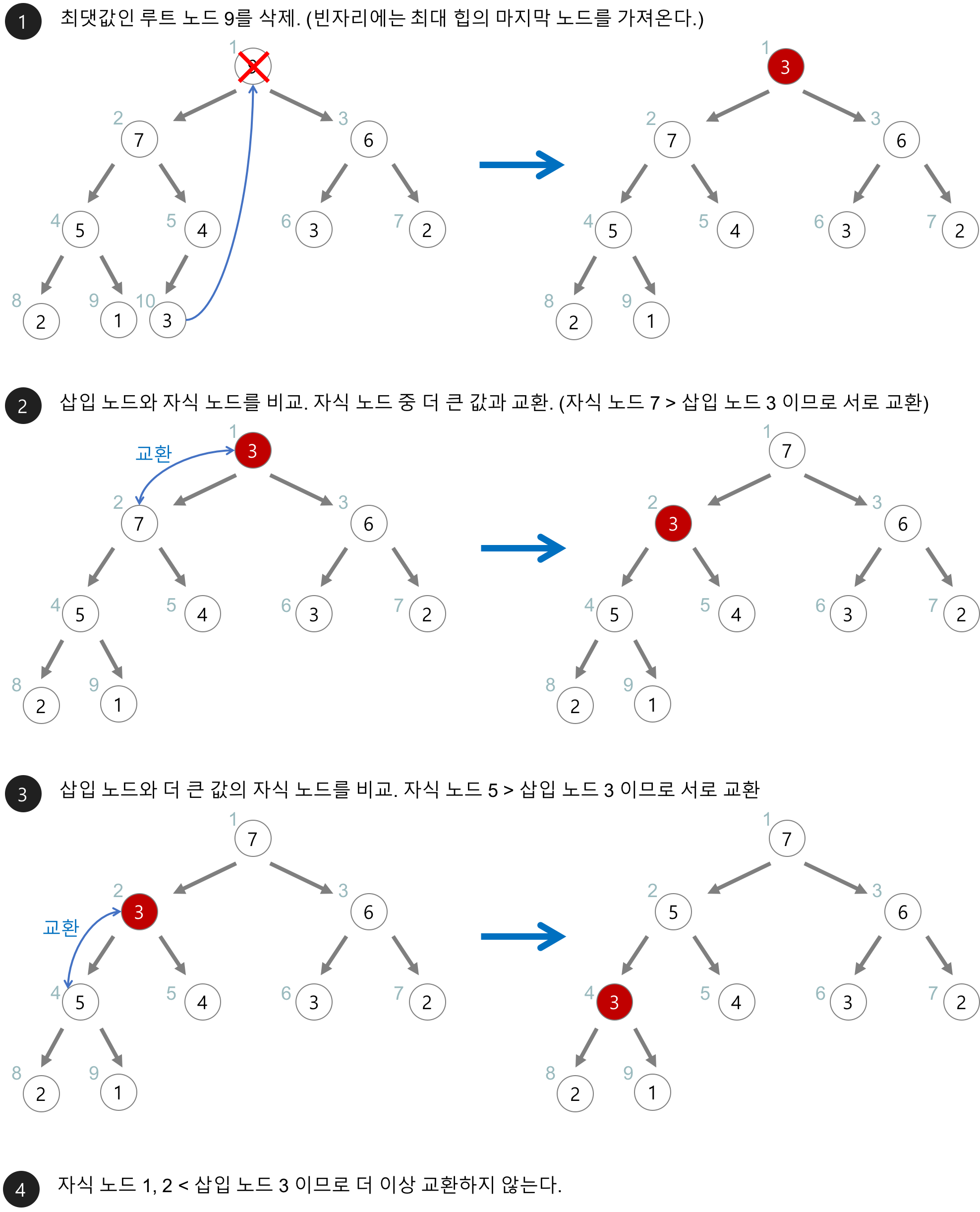
힙 삭제
최대힙에서 최대값은 루트 노드이므로 루트 노드가 삭제된다. 삭제된 루트 노드에는 힙의 마지막 노드를 가져오고 힙을 재구성한다.
우선순위 큐
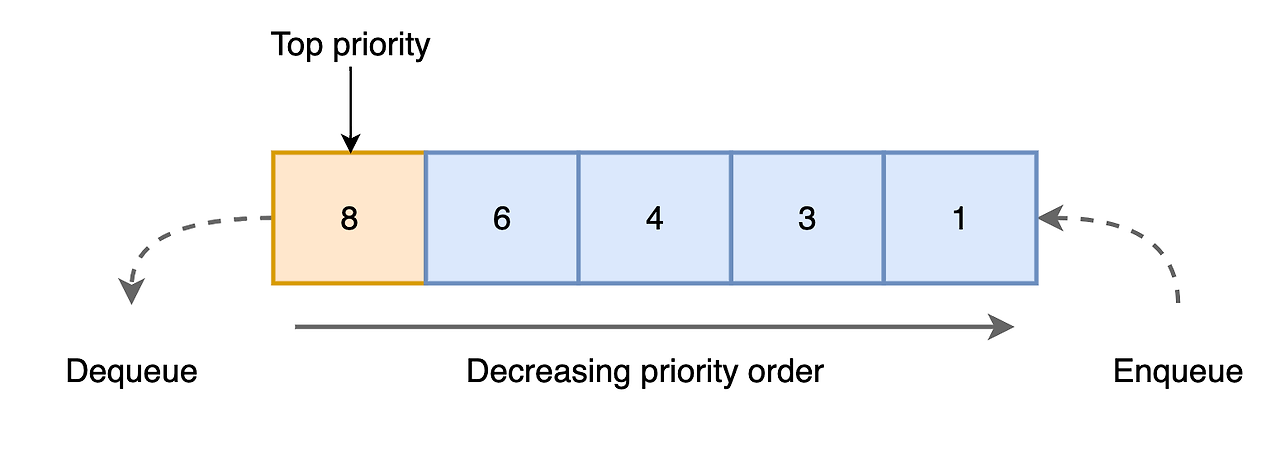
우선순위 큐는 우선순위를 가진 항목들을 저장하는 큐로 FIFO 순서가 아닌 순위가 높은 데이터가 먼저 나가는 자료구조를 말한다. 일반적으로 힙을 이용하여 구현한다.
맵
key, value 한 쌍으로 이루어진 자료구조이다. 순차적으로 해당 요소 값을 구하지 않고 key를 통해 value를 얻는다. 값은 중복될 수 있으나 key는 고유한 값을 가져야 하며 순서를 유지하지 않는다.
셋
수학에서의 집합과 같은 개념으로 동일한 자료형을 모아놓은 자료구조를 말한다. 집합의 모든 원소는 중복이 허용되지 않는다. 삽입, 삭제, 탐색의 세 가지 연산을 지원한다.
해시 테이블
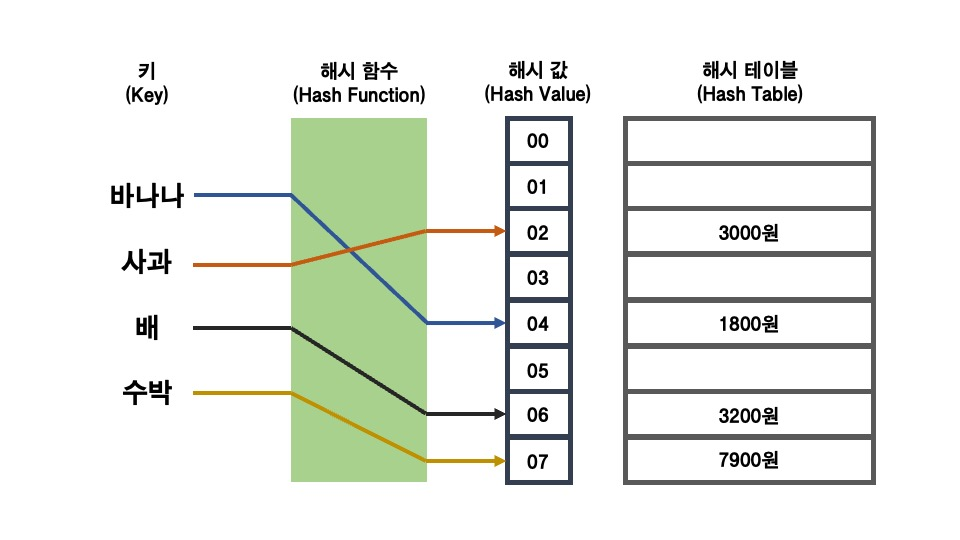
해시 테이블은 데이터가 저장되는 곳으로, 해시 함수를 통해 산출된 해시 값을 인덱스를 하여 해당 데이터를 저장한다.
- 해시 함수
- 주어진 데이터를 고유한 숫자값인 해시값으로 표현해주는 함수이다.
참고
https://adjh54.tistory.com/325
https://velog.io/@kai6666/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%9E%98%ED%94%84-Graph
https://leejinseop.tistory.com/43
https://gmlwjd9405.github.io/2018/08/13/data-structure-graph.html
https://velog.io/@kwontae1313/%ED%8A%B8%EB%A6%ACTree%EC%97%90-%EB%8C%80%ED%95%B4%EC%84%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EC%9E%90
https://gmlwjd9405.github.io/2018/08/12/data-structure-tree.html
https://velog.io/@kku64r/rbtree
https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
https://velog.io/@gnwjd309/data-structure-heap
https://myvelop.tistory.com/153
https://suyeon96.tistory.com/31
https://yoongrammer.tistory.com/81
https://healthcoding.tistory.com/51
https://jina-developer.tistory.com/101
https://gbdai.tistory.com/16
