삽입 정렬(Insertion Sort)

삽입 정렬이란?

자료 배열의 모든 요소를 앞에서부터 차례대로 이미 정렬된 배열 부분과 비교하여, 자신의 위치를 찾아 삽입함으로써 정렬을 완성하는 알고리즘이다. 매 순서마다 해당 원소를 삽입할 수 있는 위치를 찾아 해당 위치에 삽입한다.

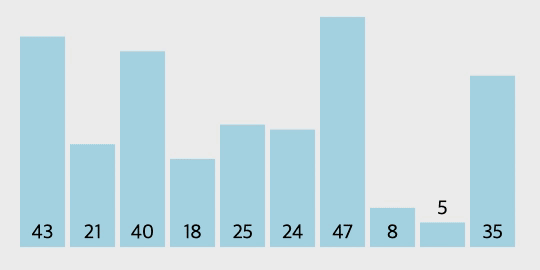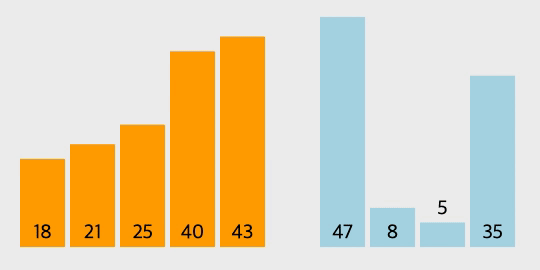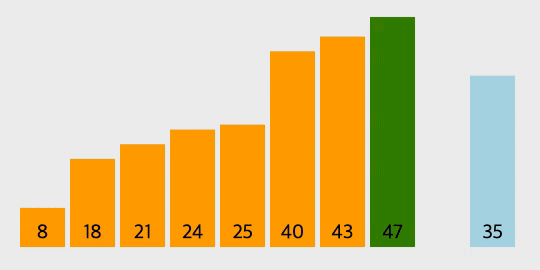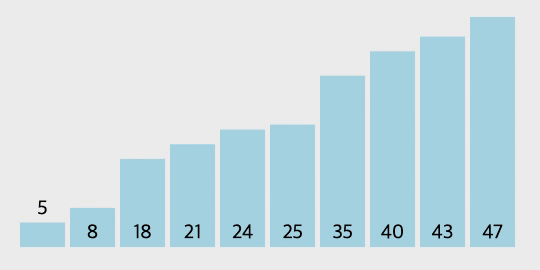
삽입 정렬의 과정

• 삽입 정렬은 두 번째 자료부터 시작하여 그 앞(왼쪽)의 자료들과 비교하여 삽입할 위치를 지정한 후 자료를 뒤로 옮기고 지정한 자리에 자료를 삽입하여 정렬한다.
  

자바 구현 코드

public static void insertionSort(int[] arr) {
	for (int i = 1; i < arr.length; i++) {
    	//선택 데이터
        int key = arr[i];
        //비교 데이터
        int j = i - 1;
        
        while (j >= 0 && arr[j] > key) {
        	arr[j + 1] = arr[j];
            j--;
        }
        arr[j + 1] = key;
    }
}

삽입 정렬의 특징

• 배열 내에서 교환하는 방식이어서 공간 복잡도는 O(1)이고 원소를 교환할 때 쓰일 임시변수 정도의 추가공간만 필요하기 때문에 제자리 정렬임
• 중복된 키 값의 순서가 정렬 후에도 유지되므로 안정 정렬임 (비교대상의 우너소가 새로운 원소보다 클 때만 한자리 뒤로 이동시키므로 동일한 원소의 우선순위를 처음 정렬과 동일하게 유지)
• 선택이나 버블 정렬보다 상대적으로 빠름
• 평균, 최악의 시간 복잡도가 O(n^2)임

장단점

• 장점
  • 안정한 정렬 방법임
  • 레코드 수가 적을 경우 알고리즘 자체가 간단하여 다른 복잡한 알고리즘에 비해 유리할 수 있음
  • 대부분이 이미 정렬되어 있는 경우에 매우 효율적일 수 있음
• 단점
  • 비교적 레코드의 이동이 많음
  • 레코드 수가 많고 레코드 크기가 클 경우에는 부적합함

시간 복잡도 & 공간 복잡도

• 최선의 경우
  • 비교 횟수
    • 이동 없이 1번의 비교만 이루어짐
    • 외부 루프는 n - 1번
      따라서 O(n)
• 최악의 경우(입력 자료 역순의 경우)
  • 비교 횟수
    • 외부 루프 안의 각 반복마다 i번이 비교 수행
    • 외부 루프 : (n - 1) + (n - 2) + ... + 2 + 1 = n(n - 1) / 2 = O(n^2)
  • 교환 횟수
    • 외부 루프의 각 단계마다 i + 2번의 이동 발생
    • n(n - 1) / 2 + 2(n - 1) = (n^2 + 3n - 4) / 2 = O(n^2)
      따라서 O(n^2)
• 평균
  평균의 경우에는 O(n^2)

참고

https://github.com/GimunLee/tech-refrigerator/blob/master/Algorithm/%EC%82%BD%EC%9E%85%20%EC%A0%95%EB%A0%AC%20(Insertion%20Sort).md#%EC%82%BD%EC%9E%85-%EC%A0%95%EB%A0%AC-insertion-sort
https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html
https://code-lab1.tistory.com/22
https://rninche01.tistory.com/entry/%EC%A0%95%EB%A0%AC-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-01-%EC%82%BD%EC%9E%85-%EC%A0%95%EB%A0%AC
https://maramarathon.tistory.com/52
https://chamdom.blog/insertion-sort/
https://sfida.tistory.com/32