numerical system

• 컴퓨터에서의 숫자 표현은 수체계(진법 시스템)에 대한 이해를 해야한다. (특히 2진수 체계)
• Base-n system, Radix-n system으로 불리면 n은 base에 해당하는 숫자이다.

Base R system

• R은 base를 의미하며 다음과 같이 표현된다.
  $A_{base} = A_R = a_{n-1}a_{n-2}...a_1a_0a_{-1}a_{-2}...a_{-m}$
• 위의 value는 다음과 같다.
  $V(A_{base}) = V(A_R) = \displaystyle\sum_{i=-m}^{n-1}a_iR^i$

주로 사용되는 진법

• R = 10: Dec
• R = 16: Hex / 0x or 0X
• R = 8: Oct / 0o
• R = 2: Bin / 0b

code for number

positive number representation

• 컴퓨터에서는 대부분 base-2 system을 이용하여 positive integer를 표시한다.

  많은 bit가 할당될수록 큰 range의 수를 표현(구분)할 수 있다.

• 대부분이라는 말에서 알 수 있겠지만 다른 방식도 있다.
• e.g. Binary Coded Decimal(BCD): base-10 기반으로 숫자를 bit로 표시 하지만 실제 컴퓨터 내부 연산에서는 사용되지 않고 bit로 전달하는 경우 등에 많이 사용되는 일종의 encoding 방식임

Number의 구분

• 연산에 사용되는 것으로 의미 중심
• 표시 및 인식을 하는 것으로 Symbol 중심
• 후자는 code(기호)에 가까움

2진수 대체 표기 For human

• 컴퓨터에서 사용되는 2진수는 사람이 읽기에 너무 어렵기 때문에 2진수를 직접 기재하기보다 2진수로 쉽게 변환되면서도 사람이 좀 더 읽기 쉽기에 16진수(Hexadecimal Representation, HEX)를 많이 사용한다.
• 16진수 말고도 8진수로 표현하는 경우도 있지만 주로 Hex로 변환한다.

프로그래밍 언어에서 양의 정수 표현

• 여러 컴퓨터 언어에서는 unsigned라는 키워드를 붙여 positive만을 표시한다.

  • unsigned char: 8bits, 1byte
  • unsigned short(int): 16bits, 2bytes
  • unsigned long(int): 32bits, 4bytes
  • unsigned int: 32bits, 4bytes
  • unsigned long long(int): 64bits, 8bytes
    64bit computer 기준 (OS도 64bit)

산술연산

• computer는 2진수의 산술연산에 기반한다.
• 일반적으로 adder와 multiplier만으로 사칙 연산을 수행한다.
• 1bit의 operand 2개를 더하는 adder를 구현한다면 logical operation의 AND와 XOR을 이용하여 구할 수 있다.

negative number

• 컴퓨터에서 bit로 음수를 표현하는 방법은 다음과 같이 세가지가 있으며 마지막에 소개할 2's complement가 가장 널리 사용된다.

sign and magnitude

• 가장 간단한 방법으로 MSB에 sign을 나타내고 나머지 bit에 magnitude를 표시하는 방법이다.

  공학에서 magnitude는 크기 양 등을 나타내며 보통 0 이상의 양수를 value로 가진다.

• 이 방법의 단점은 +0과 -0의 표현이 각각 존재하며 logic operation으로 arithmetic operation을 구현하기 힘들다.

1's complement

what is a complement

• 기준수 A를 정했을 때 임의의 수 $m$에 대한 complement $m\prime$은 A에서 $m$을 빼서 $m\prime$이 되는 수를 말한다. 이진수에서는 A가 1이 된다.

1's complement

• positive integer 표현에서 모든 bit에 NoT 연산을 취한 것이 negative integer가 되는 방식이다.
• e.g. 011(=+3) => 100(=-3)
• 이 방법도 +0과 -0의 표현이 각각 존재한다.

2's complement

• 1's complement에서 1을 더하는 방식이다.
• e.g. 011 (=+3) => 101(=-3)
• zero에 대한 표현형이 하나가 되며 arithmetic operation을 구하기도 간단하여 주로 사용된다.

complement에 의한 subtraction

• complement를 사용하는 경우 덧셈만으로 뺄셈의 구현이 가능하다.
  $x - m = x + (A - m) - A = x + m\prime - A$
• 마지막 항의 $A$를 빼주는 동작을 고려하면 complement $m\prime$을 이용하여 덧셈으로 뺄셈을 구현할 수 있다.

carry in and carry out

carry in

• 이전 자리의 연산의 결과로 carry가 넘어온 것

carry out

• 현재 자리의 연산의 결과로 carry가 발생한 것
• MSB에서 carry out(=end around carry)가 발생한 경우에 다음과 같이 접근한다.

1's complement

• 해당 MSB에서 carry out을 LSB에 더해주면 같은 효과이다.

2's complement

• 해당 MSB에서 carry out을 그냥 빼주면 된다.

sign and magnitude

• 그냥 더해서 처리할 수 없으므로 뺄셈을 위한 별도의 처리가 필요하다.

overflow detection for 2's complement

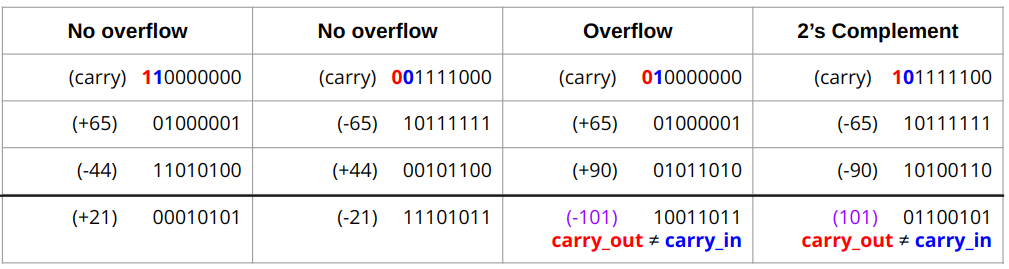
• MSB에서의 carry in과 carry out이 같을 경우는 overflow가 아니지만 이 둘이 다를 경우는 overflow이다.
• 다음은 carry in(푸른색)과 carry out(빨간색)으로 표현하여 정리한 표이다.
  

overflow and underflow

overflow

• 처리 범위를 넘어서는 연산 결과가 발생하는 경우를 가으킨다.
• overflow 발생 시 condition code register(CCR)의 overflow에 해당하는 bit가 1로 설정괸다. 즉 MSB에서 발생한 carry 값이 바로 overflow bit이다.

underflow

• 처리가능한 범위보다 작은 연산 결과가 발생하는 경우이다.
• float 등에서 처리가능한 exponent의 값이 -126 ~ 126인데 $2^{-150}$과 같은 결과가 발생하면 underflow가 발생한다고 한다.

Real number

2진수로 소수를 표현

• 실수를 2진수로 표현하는 방법은 다음과 같다.

1. 10진수 소수값에 2를 곱함
2. 2를 곱한 결과가 1미만이면 0을 기록
3. 1을 초과할 경우 1을 기록하고 결괏값에서는 1을 뺀다.
4. 결과값이 1인 경우 1을 기록하고 변환을 끝내고 1이 아니면 2번 단계로 다시 올라간다.

   위의 글을 보면 어렵게 느껴질테지만 사실 저 방식은 10진수를 2진수로 바꾸는 방법에서 $2^{-n}$으로 확장한 것이다.

• 실수의 2진수 표현을 bit로 표현하는 방법은 크게 다음과 같이 나뉜다.

Fixed-point representation

• 기존의 integer를 표현하던 방식을 그대로 사용하여 특정 자리의 bit는 integer부분 나머지 부분은 소수부분을 표현한다.
• 이는 physics 분야의 연산을 할 때 범위가 제한되어 있어 낭비가 심해서 잘 쓰이지 않는다.

  planck's constant는 $6.63 \times 10^{-34}$ joule-seconds이고 avogadro's constant는 $6.02 \times 10^{23}$이다. 즉 physics 분야의 연산은 큰 수 또는 많이 작은 수를 다룬다.

Floating-point representation

• 소수점 위치가 변경되는 방식으로 scientific notation에 기반한 방식이다.
• 일반적으로 computer에서 사용되는 방식이고 Digital signal processing(DSP) system에서만 fixed-point representation이 사용된다.
• 소수점이 고정되지 않지만 유효숫자 자리수는 고정되기 때문에 큰 수를 표현할 때 precision이 떨어지고 정밀하게 사용될 때에는 range가 작아진다. 즉 range와 precision은 trade-off 관계이다. 하지만 fixed-point representation과 비교하면 두 가지 측면에서 우수하다.
• 프로그래머들은 float라 부르며 real number의 다른 이름으로 인식될 정도로 널리 사용된다.
• 이 방법은 IEEE에 의해 IEEE754로 표준화되어 있다.

참고: scientific notation

• 과학에서 숫자를 표기할 때의 규칙이다.
• $a \times 10^n (1\leq a \lt 10)$

IEEE754

• bit 길이를 3 부분으로 나누어 sign(부호), exponent(지수), mantissa(가수)를 표현하는 규약이다.

Mantissa

• 표현가능한 유효 숫자에 해당하며 precision을 결정한다.

Exponent

• 수치의 크기를 결정한다.

Base

• 몇 진수인지를 표현한다.

IEEE754 변환 과정

1. 숫자를 이진수로 바꾼다.
2. 부동소수점으로 표현한다.
3. 컴퓨터의 각 sign, exponent, mantissa를 구한다.
   e.g.
4. -0.04 => -0.00001010001111010111....
5. -0.00001010001111010111.... => -1.01000111101011100001010 * $2^{-5}$
6. s = 1(negative)
   m = ($01000111101011100001010_2$) = $2348810_{10}$
   e = ($01111010_2$) = ($122_{10}$)

NAN

• Not a Bumber의 줄임말으로 0으로 나누는 등의 결과와 같이 숫자가 아닌 특정 경과도 표시하기 쉽다.

code for number(symbol)

code

• 일상 생활에서 사용되는 문잔 숫자를 컴퓨터가 인식하기 위해 기호화한 것이다.
• 컴퓨터가 사람들이 사용하는 number를 표현하고 인식하기 위한 코드들은 2가지가 있다.

1. Internal representation: 계산이 효과적으로 이루어지느데 집중하는 representation
2. external representation: 숫자를 표현하거나 입력장치로부터 숫자 기호를 압력받을 때 사용되는 representation

• 여기서 다루는 code는 external representation이다.

Binary coded decimal system

• 각 자리의 digit을 각각 16진수로 변경하고 그 16진수를 4bit의 binary로 변환하여 표현하는 것이다.
• 출력에서는 사람들이 이해하기 쉬운 10진수로 표현되어야 하기 때문에 잘 활용된다.
• 8-4-2-1 코드라고도 불린다.

  BCD는 각 digir을 4bit의 binary로 표현하는 것이지만 4bit를 기억하기 위해 16진수를 중간에 도입했다.

• e.g. 23 => 0010 0011
• 과거 2세대 컴퓨터는 BCD를 사용하였지만 현재 내부적으로 BCD를 쓰는 컴퓨터는 없다. 하지만 encoding등에서 해당 개념을 많이 차용한 경우가 많기 때문에 어떻게 변화하는지 아는 것이 좋다.

장단점

장점

• 10진법에서 2진법으로 가장 쉽게 변환이 가능하다.

단점

• bit 낭비가 심하다. 10진수의 1자리를 표현하는데 16개를 구분가능한 4bit를 할당하고 있다.
• complement를 구하기 힘들다.

---

Extended binary coded decimal interchange (EBCDI) code

• BCD code를 문자 기호에 대한 코드 추가 등 확장하여 8비트로 표현하는 방식이다.
• 상위 4비트가 Zine, 하위 4비트는 BCD이다.
• sign은 가장 하위자리의 Zone으로 표현된다.

  • sign은 1100

  • sign은 1101

• e.g. $+897_{10}$ => $1000 1001 0111 1100$

현재는 ASCII에 밀려 컴퓨터 내부적으로는 사용되지 않는다.(연산용이 아니라는 뜻임)

단 숫자를 표현하는 code로서 EBCDIC은 숫자를 disply 또는 input 또는 통신으로 주고받는 등의 경우 등의 차용되며 사용되는 경우가 아직도 존재한다.

Excess-3 code

• BCD code는 2진수 표현애 가깝고 encoding에 용이하나 complement에 대한 계산 및 처리가 까다로워서 이를 보완하기 위해 만든 code이다.
• BCD code에 +3을 해서 9의 보수를 매우 쉽게 얻을 수 있다.(1's complement를 하면 자동으로 9의 보수를 얻게 된다.)

---

Gray code

• BCD code에 인접하는 bit를 XOR로 연산하여 만들어진 코드
• 0에서 9까지 순환적으로 변할 때 각 과정마다 오직 한 비트만 변화되어 순환적으로 값이 입력될 경우 에러를 찾기 쉬우며 변경할 bit가 적다는 장점을 가진다.
• A/D변환, I/O device 등에 많이 사용된다.
• 2-bit Gray code는 quadrature encoding이라고 불리며 2개의 센서만으로 모터의 회전축이 얼마나 그리고 어느 방향으로 회전했는지와 더불어 회전 속도 등을 확인할 수 있어서 knob와 같은 장치 즉 제어에서도 사용 가능하다.
• 2개의 센서로 구성된 quadrature encoder의 경우 $\frac{1}{4096}$ 회전을 감지할 수 있다.
• $\frac{1}{4096}$ 회전 resolution을 absolute position encoder로 만드려면 12개의 센서가 필요하다. ($2^{12} = 2^2 \times 1024 = 4096)

BCD, Express-3 and Gray code

• 다음 table은 숫자를 표현하는 3가지 code이다.

Decimal	BCD	Express-3	Gray
0	0000	0011	0000
1	0001	0100	0001
2	0010	0101	0011
3	0011	0110	0010
4	0100	0111	0110
...
9	1001	1100	1101

---

reference
1. CE mkdocs