
🟢 A* (A Star) 알고리즘이란?
다익스트라 알고리즘을 확장하여 만들어진 경로 탐색 알고리즘입니다. 드론이나 로봇 차량의 인공지능 주행을 구현하기 위해 개발되었습니다. 에이스타 알고리즘이라고 읽습니다.
최단 경로를 찾아내는 그래프 탐색 알고리즘이며 다익스트라 알고리즘과의 차이점은 목표 노드 n까지의 휴리스틱(Heuristic) 거리 측정값이 h(n)도 사용한다는 점입니다.
🟢 A* 알고리즘의 비용 계산 방법
f(n) : g(n)과 h(n)을 더한 총 비용 (Heuristic cost function)
g(n) : 출발 노드에서 현재 노드 n까지 도달하기 위한 최단 비용
h(n) : 현재 노드 n에서 목표 노드까지의 예상 이동 비용 (Heuristic 거리 측정값)
이때, 인접한 노드 사이의 거리는 10으로 정하고, 대각선 방향의 경우 피타고라스를 활용하여 14로 정합니다. (정확히는 14.14...이지만, 빠른 계산을 위해 소수점 0.14...는 생략)
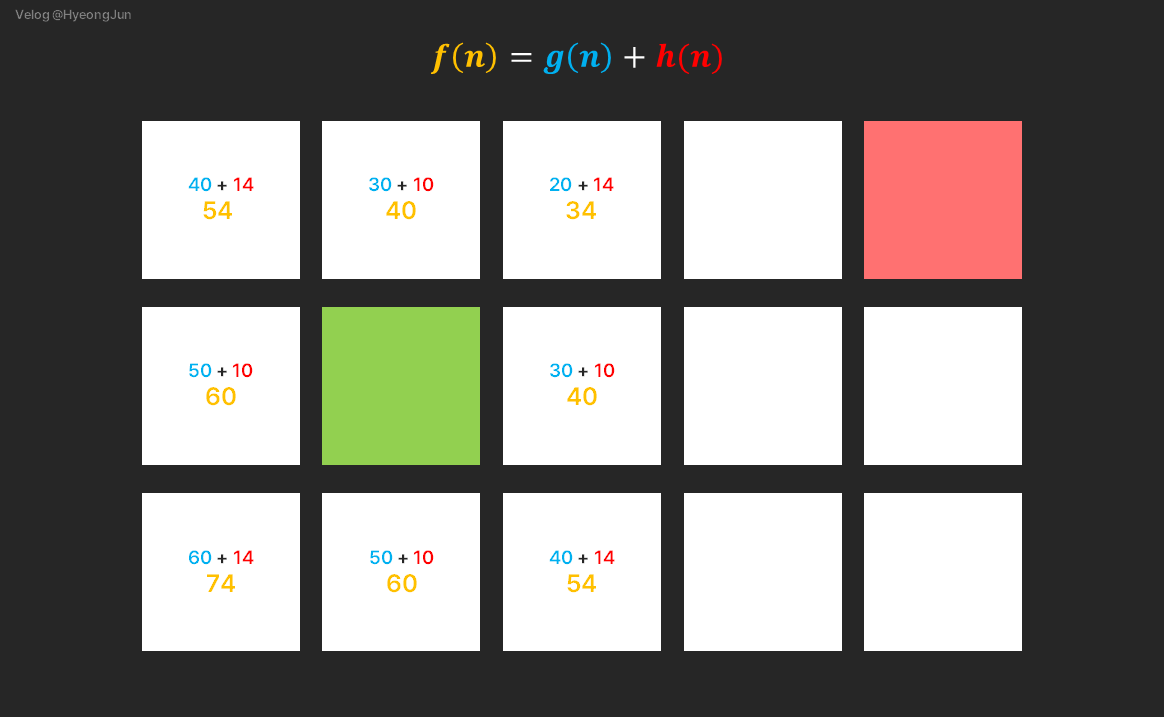
위 그림에서 초록 -> 빨강의 최단 경로를 A* 알고리즘을 통해 구해보도록 하겠습니다.
알고리즘의 개념을 적당히 이해하셨다면, 노란색 숫자가 가장 작은 오른쪽 위 대각선 방향 34로 가면 된다는 것을 알겠지만, 어떻게 저 숫자가 나왔는지 체크해봅시다.
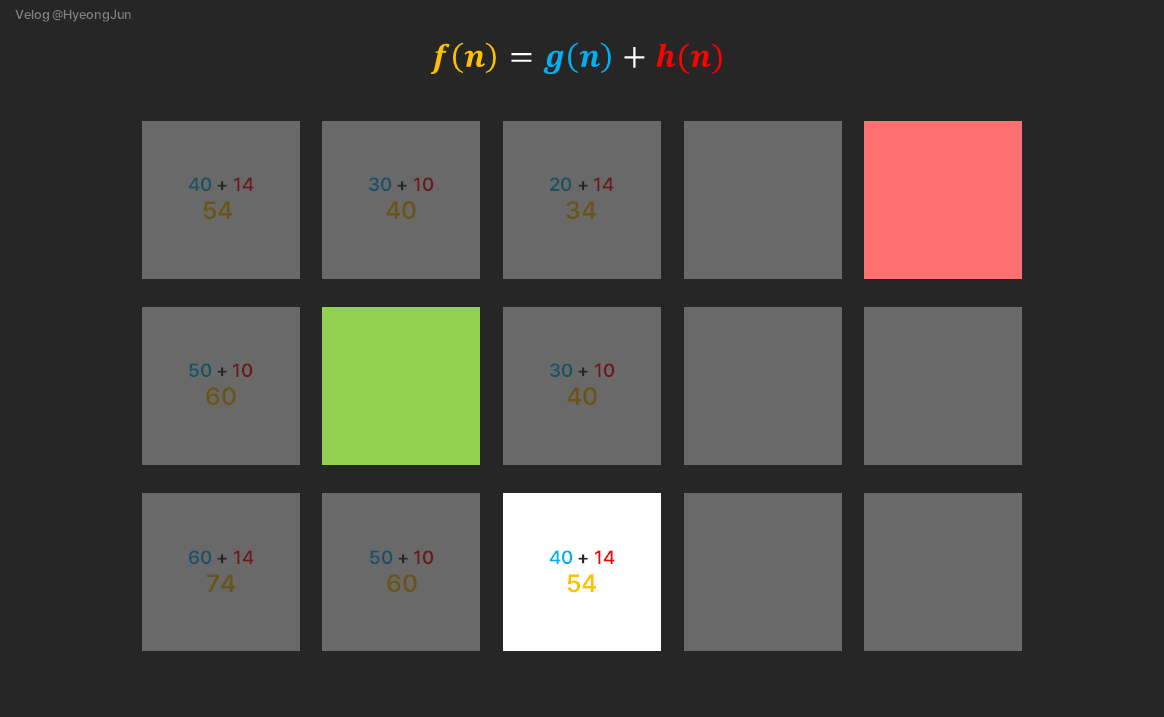
오른쪽 아래 대각선 방향의 f(n)을 구해보겠습니다.
먼저 g(n)을 구합니다.
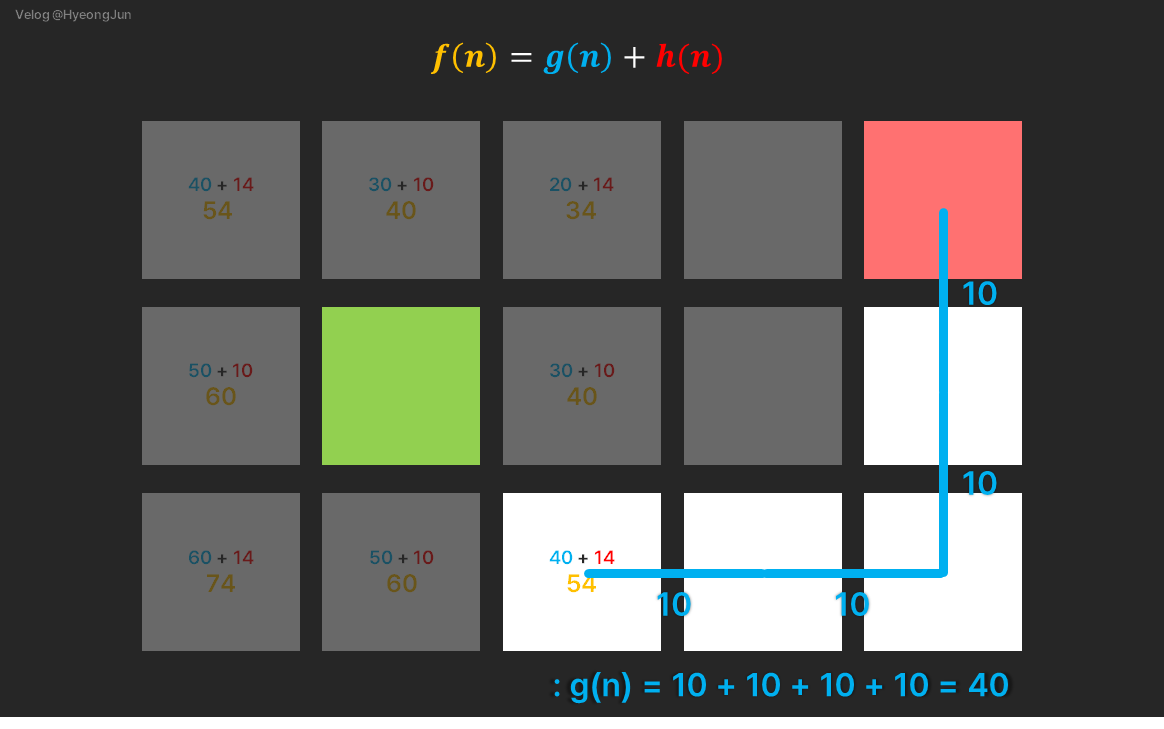
g(n)은 해당 노드에서 목적지까지의 거리이므로 가로x2, 세로x2를 더한 40이 됩니다.
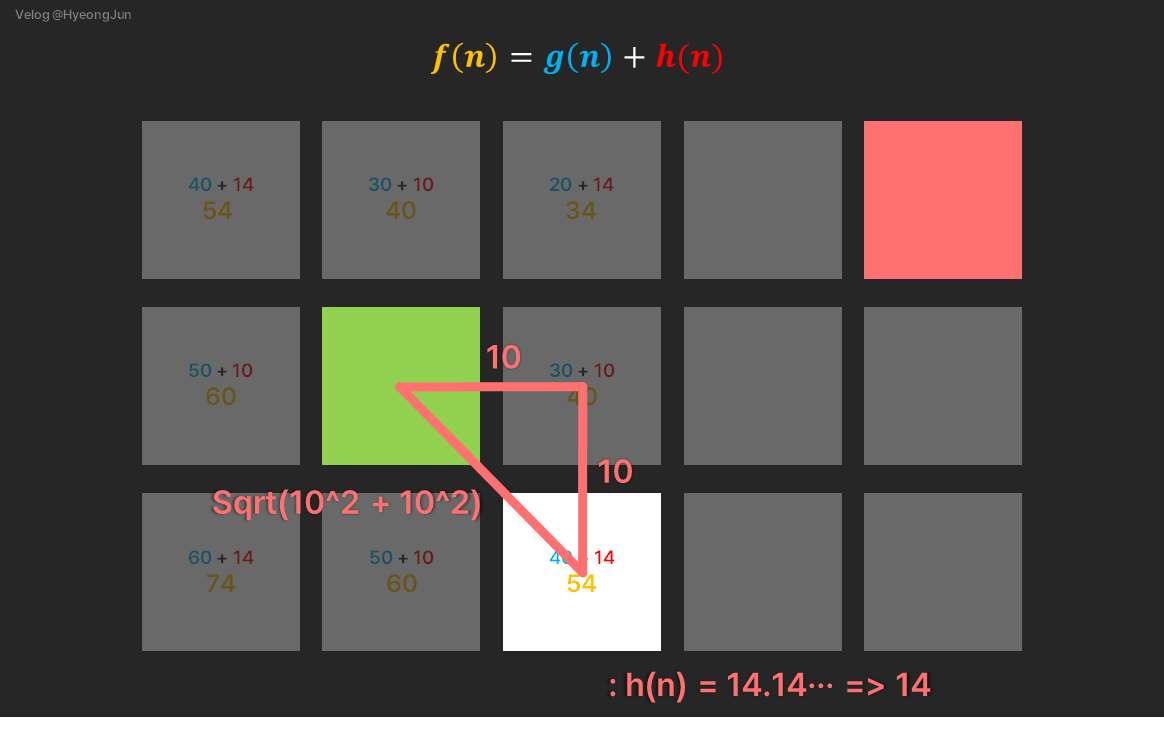
다음으로 h(n)은
이므로 14가 됩니다.
이때, f(n)의 값은 g(n)과 h(n)을 더한 54가 됩니다.
다시 위로 돌아와서, 오른쪽 위 대각선에 있는 노드를 선택하고, 그 노드를 기준으로 8칸 중 채워지지 않은 노드들의 f(n)을 구합니다.
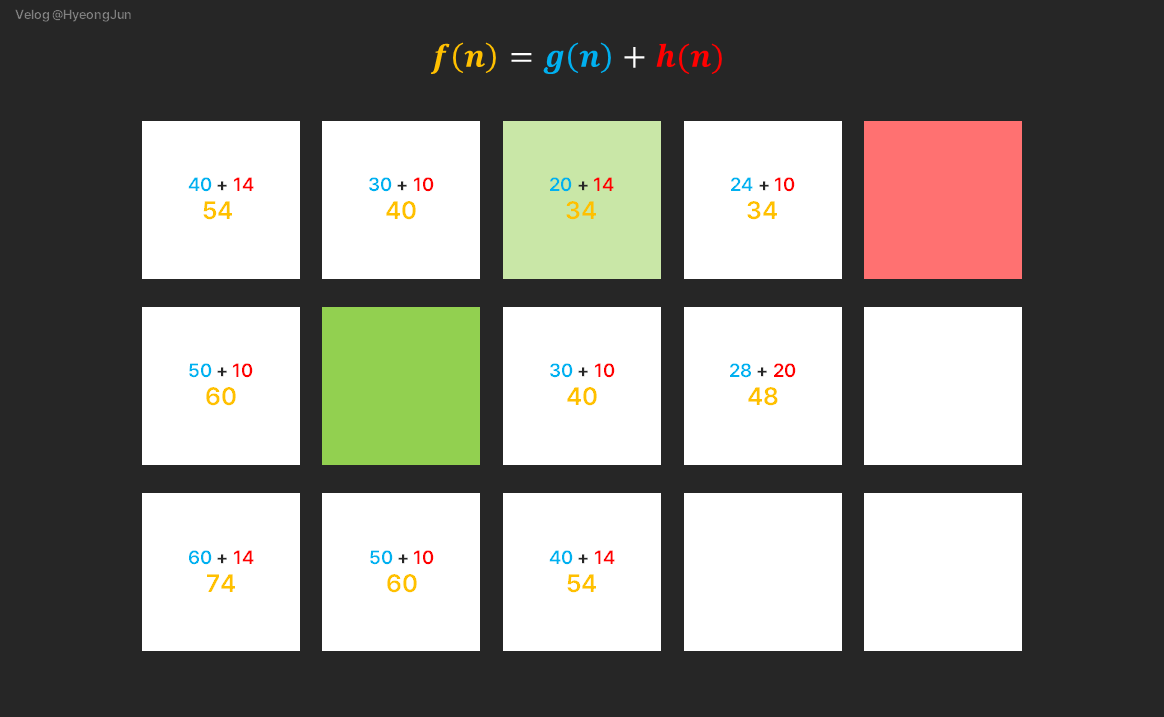

위 과정을 통해 최단 경로를 구할 수 있습니다.
🟢 시간 복잡도
V : 정점 수
E : 간선 수
보통 격자 맵에서는 E ~= 4V (상하좌우 이동 가능)
1. 최악의 경우 (Worst-case)
- 휴리스틱이
0이면 사실상Dijkstra알고리즘과 같음
2. 최선의 경우 (Best-case)
- 휴리스틱이 아주 잘 맞으면 거의 직선으로 탐색
3. 평균적
- 휴리스틱 품질에 따라
Dijkstra보다 빠름 - 특히 격자 탐색에서는
O(V)보다 훨씬 줄어듦
🟢 다른 탐색 알고리즘과의 비교
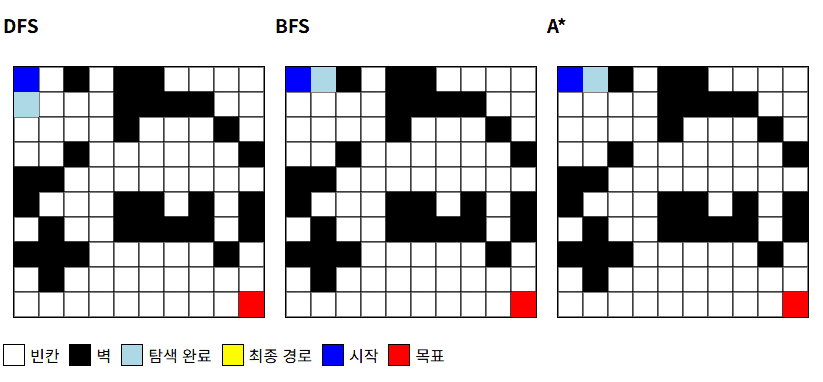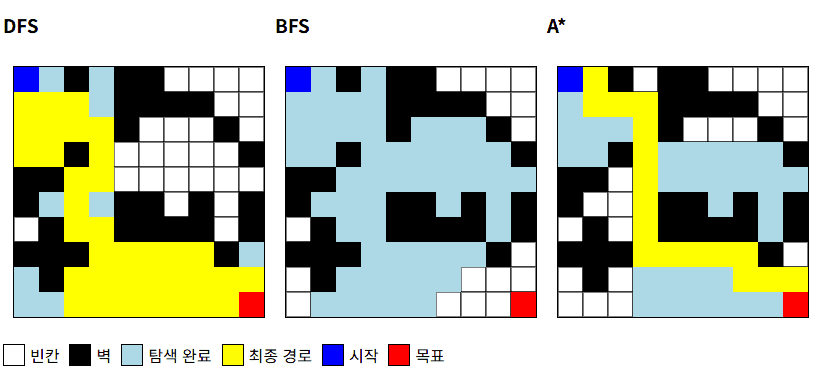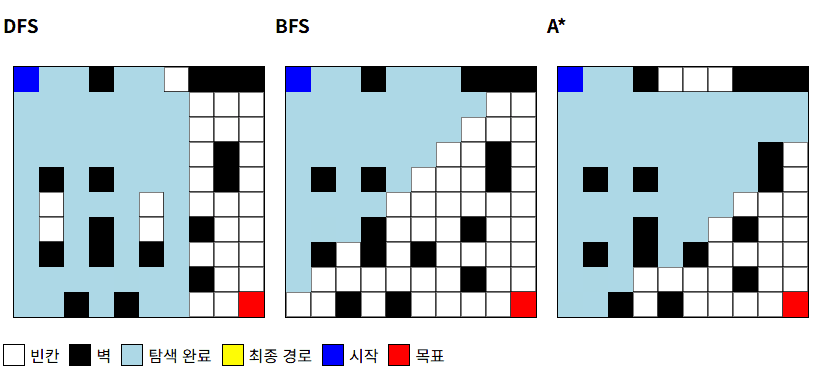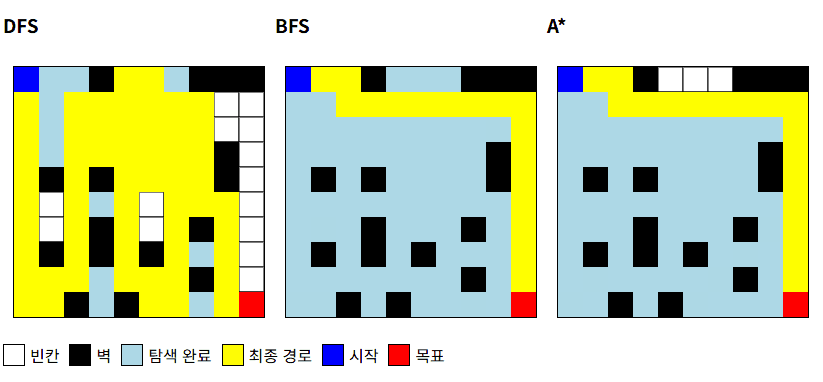
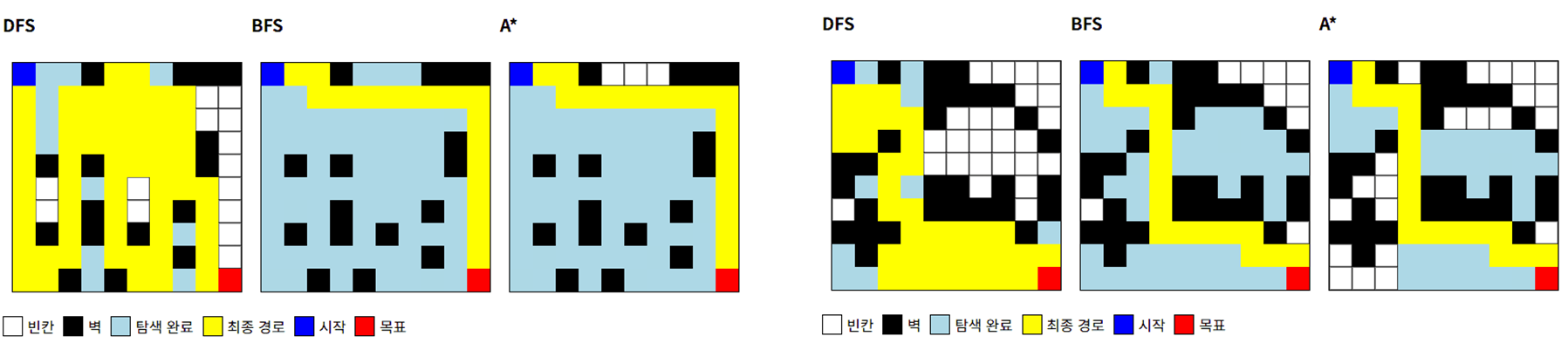
위 GIF 및 결과 사진을 통해 DFS, BFS, A*의 특징이 잘 드러납니다.
DFS: 우연히 긴 길을 가게 됨, 비효율적인 경로BFS: 최단 경로 보장, 탐색 영역이 큼A*: 최단 경로 보장, 탐색 영역이 적음
| 알고리즘 | 방식 | 특징 | 장점 | 단점 | 시간복잡도 |
|---|---|---|---|---|---|
| DFS (Depth-First Search) | 한 방향으로 끝까지 파고든 후, 막히면 되돌아옴 (스택/재귀) | 경로 탐색 시 깊이 우선 | - 구현이 간단 - 재귀로 직관적 표현 가능 - 경로 존재 여부 빠르게 확인 가능 | - 최단 경로 보장 X - 무한 그래프에서 무한 루프 위험 | O(V+E) |
| BFS (Breadth-First Search) | 시작점에서 가까운 노드부터 탐색 (큐) | 레벨 단위 탐색 | - 최단 경로 보장 (가중치 동일한 경우) - 전체 탐색에 강함 | - 메모리 사용량 큼 (큐에 많은 노드 저장) | O(V+E) |
| Dijkstra | BFS + 가중치 고려 (우선순위 큐) | 최소 비용 경로 탐색 | - 모든 간선이 양수일 때 최단 경로 보장 | - 음수 가중치 처리 불가 - 휴리스틱 없음 => 탐색 범위 큼 | O(E log V) |
| A* (A-star) | Dijkstra + 휴리스틱 | f(n) = g(n) + h(n) 기준으로 탐색 | - 휴리스틱이 좋으면 매우 효율적 - 최단 경로 보장 (admissible h 사용 시) | - 휴리스틱 설정이 어렵고 부정확하면 느려짐 | O(E log V) (최악은 Dijkstra와 동일) |
| Greedy Best-First Search | 휴리스틱 h(n)만 사용 | 목표에 가까운 노드 우선 탐색 | - 빠르게 답을 찾음 | - 항상 최적 경로 보장 X | O(E log V) |
🟢 구현 코드
class Node {
constructor(x, y, g = 0, h = 0, parent = null) {
this.x = x; // 위치 x
this.y = y; // 위치 y
this.g = g; // 시작점 ~ 현재까지 비용
this.h = h; // 휴리스틱 (현재 ~ 목표)
this.f = g + h; // 총 비용
this.parent = parent; // 경로 역추적용
}
}
// 맨해튼 거리 휴리스틱
function heuristic(a, b) {
return Math.abs(a.x - b.x) + Math.abs(a.y - b.y);
}
function aStar(grid, start, goal) {
const openSet = [];
const closedSet = [];
const startNode = new Node(start.x, start.y);
const goalNode = new Node(goal.x, goal.y);
openSet.push(startNode);
while (openSet.length > 0) {
// f 값이 가장 작은 노드를 선택
openSet.sort((a, b) => a.f - b.f);
const current = openSet.shift();
closedSet.push(current);
// 목표에 도착하면 경로 반환
if (current.x === goalNode.x && current.y === goalNode.y) {
const path = [];
let temp = current;
while (temp) {
path.push([temp.x, temp.y]);
temp = temp.parent;
}
return path.reverse();
}
// 상하좌우 이웃 탐색
const directions = [
[0, -1],
[0, 1],
[-1, 0],
[1, 0],
];
for (let [dx, dy] of directions) {
const nx = current.x + dx;
const ny = current.y + dy;
// 지도 범위 확인
if (nx < 0 || ny < 0 || nx >= grid.length || ny >= grid[0].length)
continue;
if (grid[nx][ny] === 1) continue; // 벽은 패스
// 이미 탐색한 노드인지 확인
if (closedSet.some((n) => n.x === nx && n.y === ny)) continue;
const g = current.g + 1;
const h = heuristic({ x: nx, y: ny }, goalNode);
const neighbor = new Node(nx, ny, g, h, current);
const existing = openSet.find((n) => n.x === nx && n.y === ny);
if (!existing || g < existing.g) {
openSet.push(neighbor);
}
}
}
return []; // 경로 없음
}
// ──────────────── 테스트 ────────────────
const grid = [
[0, 0, 0, 0, 0],
[1, 1, 0, 1, 0],
[0, 0, 0, 1, 0],
[0, 1, 1, 0, 0],
[0, 0, 0, 0, 0],
];
const start = { x: 0, y: 0 };
const goal = { x: 4, y: 4 };
const path = aStar(grid, start, goal);
console.log('최단 경로:', path);Reference
https://namu.wiki/w/A*%20%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://recall.tistory.com/40#google_vignette
