레드 블랙트리의 속성 복습하기!
속성
- 루트 노드는 Black
- Red 의 자녀들은 Black ( = Red 는 연속적으로 존재할 수 없다 )
- 임의의 노드에서 자손 nill 노드들까지 가는 경로들의 Black 수는 같다 ( 자기 자신은 카운트에서 제외 )
삭제 방식
- 삭제 전 RB 트리 속성을 만족한 상태
- 일반적인 BST의 삭제 방식과 동일
- 삭제 후 RB 트리 위반 여부 확인
- RB 트리 속성을 위반했다면 재조정
- RB 트리 속성을 다시 만족
삭제되는 색
RB 트리에서 노드를 삭제할 때 어떤 색이 삭제 되는지가 속성 위반 여부 를 확인할 때 매우 중요
-
삭제하려는 노드의 자녀(Nil 노드 제외) = 없다/1개
: 삭제되는 색 = 삭제되는 노드의 색 -
삭제하려는 노드의 자녀 = 2개
: 삭제되는 색 = 삭제되는 노드의 successor 의 색
- 삭제되는 색 = Red
: 어떠한 속성도 위반하지 않음
- 삭제되는 색 = Black
:#2,#4,#5속성 위반할 수 있다
속성 위반
#2속성 위반 (삭제 색 = Black)- 해결 : 루트 노드를 Black으로 바꿔주기
-
#5속성 위반 (삭제 색 = Black)
: 삭제되는 색이 Black 일때 특수한 상황을 제외하면#5속성을 항상 위반-
해결 :
#5속성을 다시 만족시키기 위해 삭제 색의 위치를 대체한 노드에extra black을 부여 -
extra black을 부여받은 노드는doubly black,red-and-black이 된다.
-
extra black 해결
-
red-and-black을 Black 으로 바꾸기#4,#5를 위반한 것을 동시에 해결
-
doubly black해결총 4가지 Case 로 분류하며,
그 기준은doubly black의 형제 색 과 그 형제들의 자녀들의 색
📌plus : extra black
-
역할 : 경로에서 black 수를 카운트 할 때, 하나의 black으로 카운트
-
위치 : 삭제된 색의 위치를 대체한 노드에
extra black부여 -
doubly black :
extra black이 부여된 black 노드 -
red-and-black :
extra black이 부여된 red 노드
Case 4.
: doubly black의 오른쪽 형제가 Black
& 그 형제의 오른쪽 자녀가 Red 일때
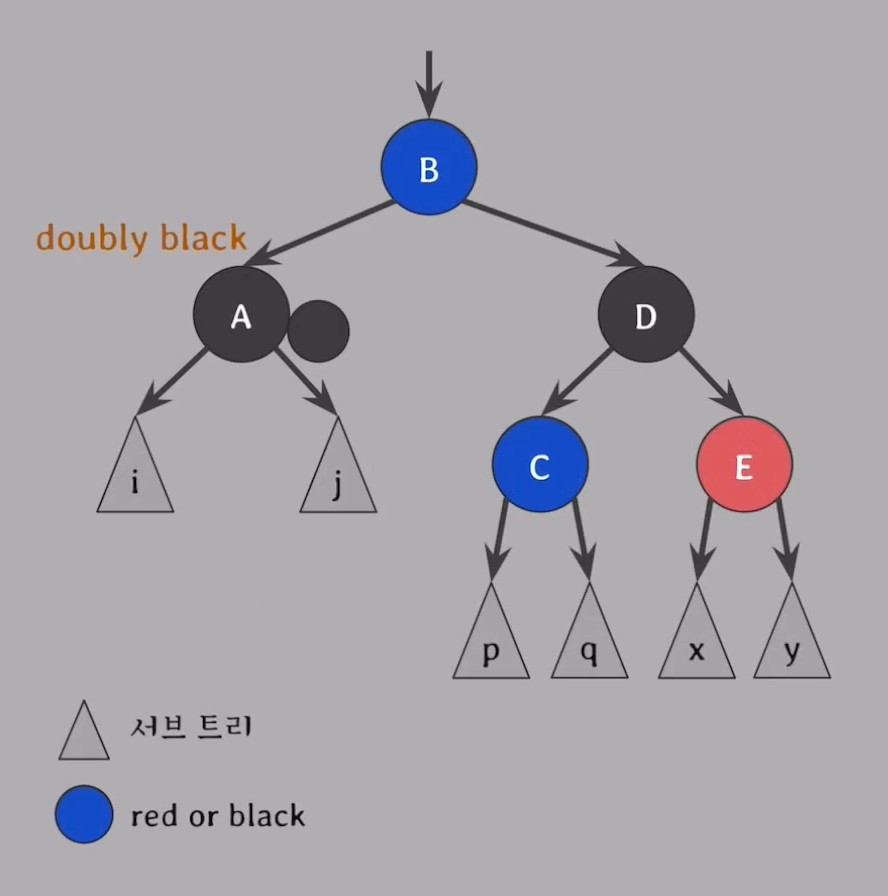
- 해결 방법
- 오른쪽 형제는 부모의 색으로 바꾸기
- 오른쪽 형제의 오른쪽 자녀는 Black, 부모는 Black 으로 바꾸기
- 부모를 기준으로 왼쪽으로 회전
( 오른쪽 왼쪽을 바꿔도 성립 )
Case 3.
: doubly black의 오른쪽 형제가 Black
& 그 형제의 왼쪽 자녀가 Red 일때
& 그 형제의 오른쪽 자녀가 Black 일때
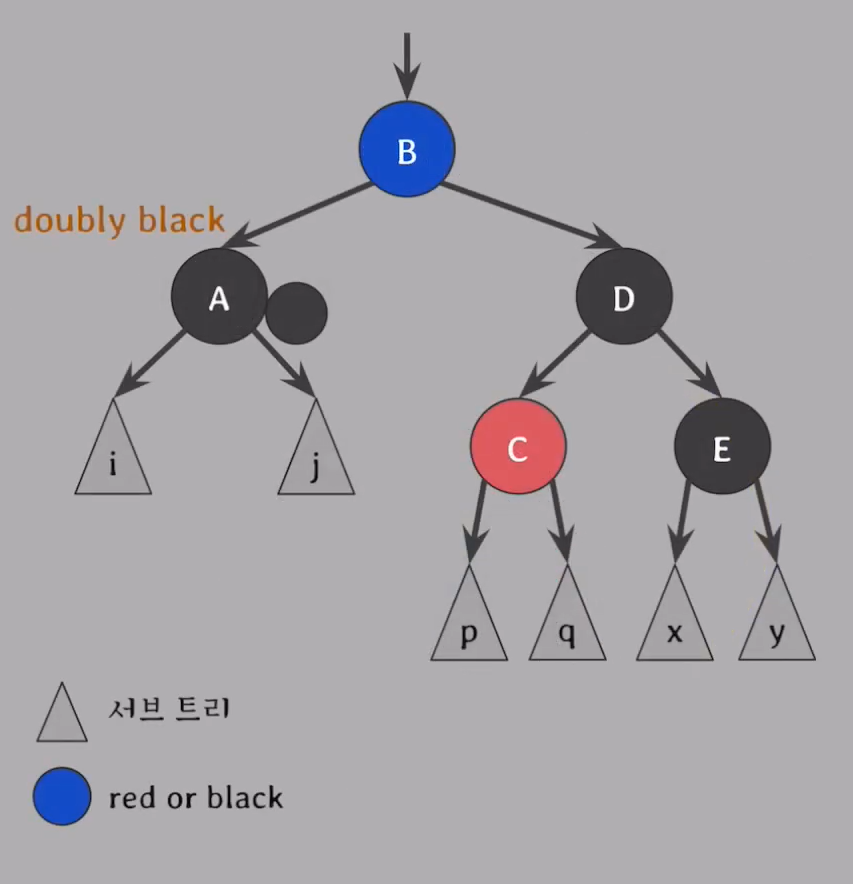
- 해결 방법
doubly black의 오른쪽 형제와 Red 자녀 색을 바꿔주기doubly black의 오른쪽 형제를 기준으로 오른쪽으로 회전- Case 4.를 적용
( 오른쪽 왼쪽을 바꿔도 성립 )
Case 2.
: doubly black의 형제가 Black
& 그 형제의 두 자녀 모두 Black
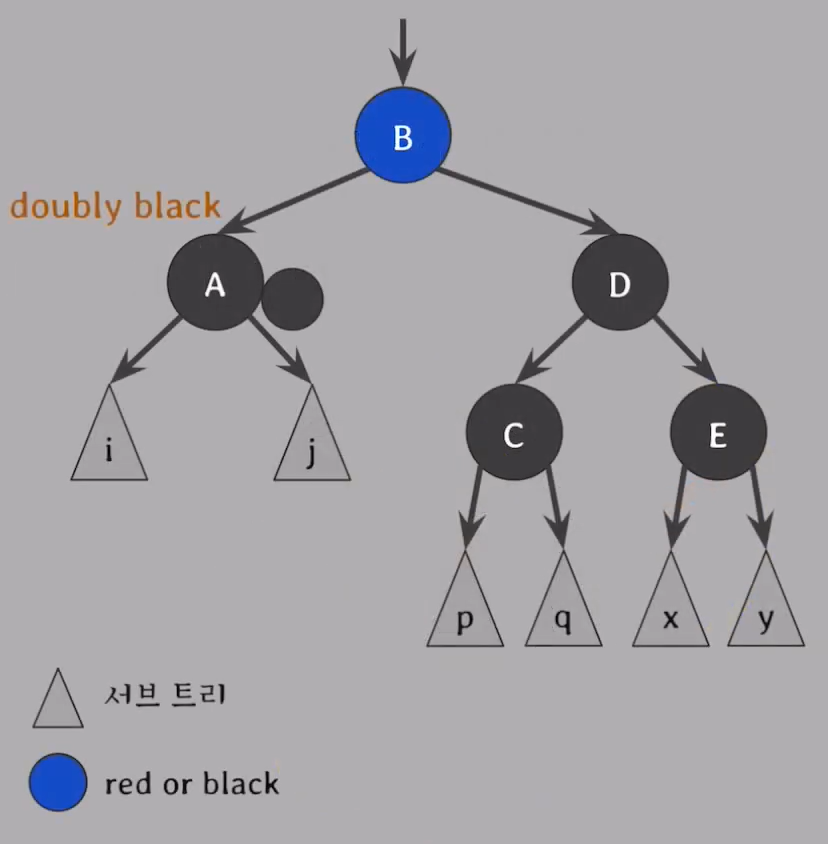
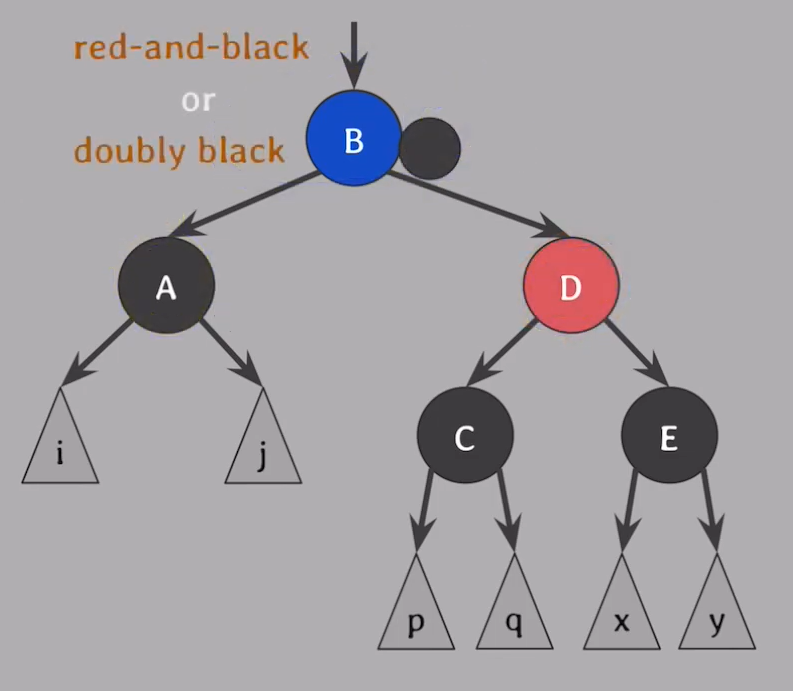
- 해결 방법 : 부모가 extra black 을 해결하도록 위임
- doubly black 의 extra black 과 그 형제의 Black을 모아 부모에게 전달
- doubly black 의 색은 Red 로 바뀜
- 부모의 색이
red-and-black혹은doubly black
3.1red-and-blackor루트노드-> Black 으로 바꿔주기
3.2doubly black-> Case 1,2,3,4 중 하나로 해결
Case 1.
: doubly black의 형제가 Red 일때
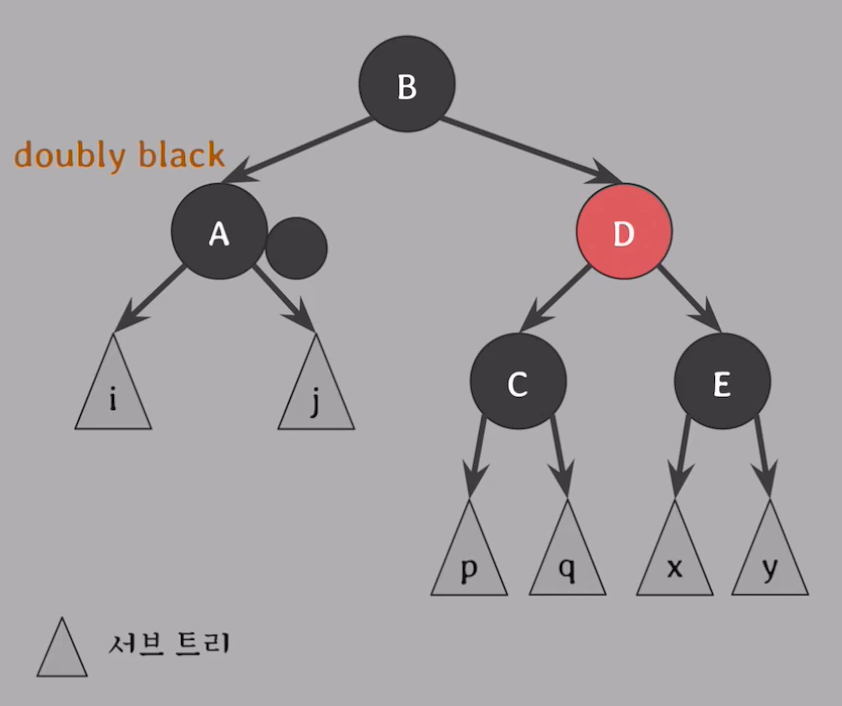
- 해결 방법
- 부모와 형제의 색 바꾸기
- 부모를 기준으로 왼쪽으로 회전
doubly black을 기준으로 Case 2, 3, 4 중 하나로 해결
( 오른쪽 왼쪽을 바꿔도 성립 )
