C# 재귀함수, Sort(정렬)
개인적인 실습이 포함되어서 틀린 내용이 있을 수 있습니다!
재귀함수
함수내에 자기자신을 호출하여 반복하여 함수를 실행하는 함수
재귀함수의 장점:
- 코드로 표현하기 어려운 경우도 직관적이고 처리가능
- 분할정복을 통한 반절 계산이 가능해서 효율 높아짐
병합정렬 : 반을 나누고 계산 반을 나누고 계산
*분할정복: 큰 문제를 작은문제로 작은문제를 더 작은문제로
제일 하위문제를 해결하여 상위 문제를 해결하는 방법
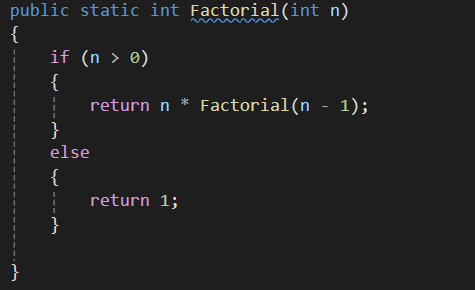
유명한 예제로 Factorial이 재귀함수를 사용하면 편리하게 작성이 된다.
알고리즘
문제 해결을 위한 과정과 논리적인 절차를 구성한 단계
1. 정확도 2. 효율성 - 이 두가지가 코딩에서의 알고리즘 설계이다.
알고리즘 조건
- 입력 : 알고리즘은 0개 이상의 입력을 가져야 함
- 출력 : 알고리즘은 최소 1개 이상의 결과를 가져야 함
- 명확성 : 수행 과정은 모호하지 않고 정확한 수단을 제공 해야 함
- 유한성 : 수행 과정은 무한하지 않고 유한한 작업 이후에 정지해야 함
- 효과성 : 모든 과정은 명백하게 실행 가능해야 함
범용적 알고리즘 - 탐색, 정렬, 경로탐색
정렬 알고리즘을 알아보겠다.
알고리즘 구현에서 필요한 4가지를 사용하여 5가지 정렬 알고리즘을 학습해보자
- 5가지 정렬 알고리즘의 컨셉 & 동작방법을 분석
- 슈도코드 또는 플로우차트 형태로 설계
- 설계를 한 내용을 토대로 코드 작성까지 진행
- 원하는대로 동작하지 않는다면, 다시 원인 분석
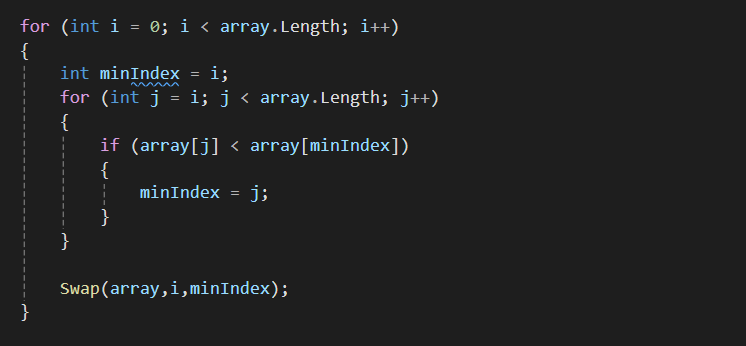
1) 선택정렬
가장 낮은 값을 선택하여 정렬하는 방법
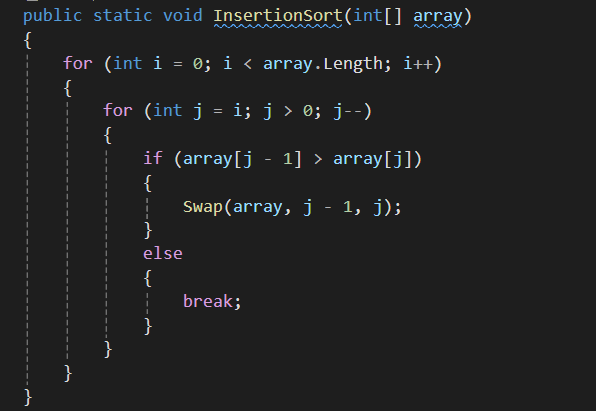
2) 삽입정렬
선택한 값을 순서에 맞게 삽입하여 정렬하는 방법
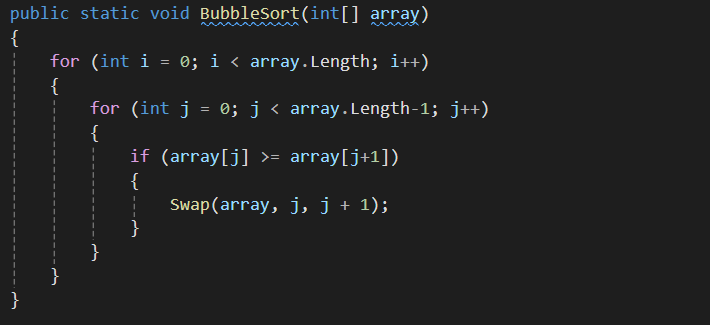
3) 버블정렬
두개의 값을 비교하여 작은쪽이 왼쪽 큰쪽이 오른쪽으로 가는 정렬
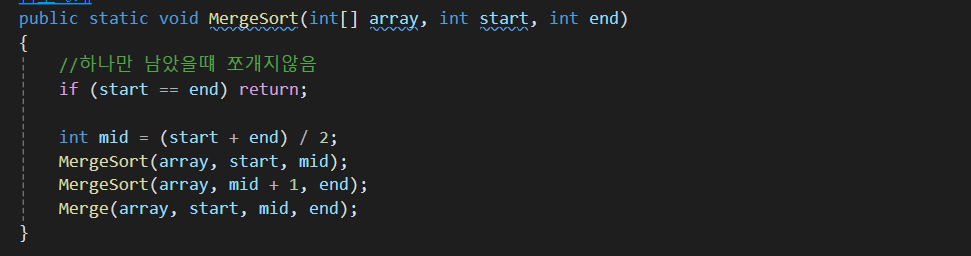
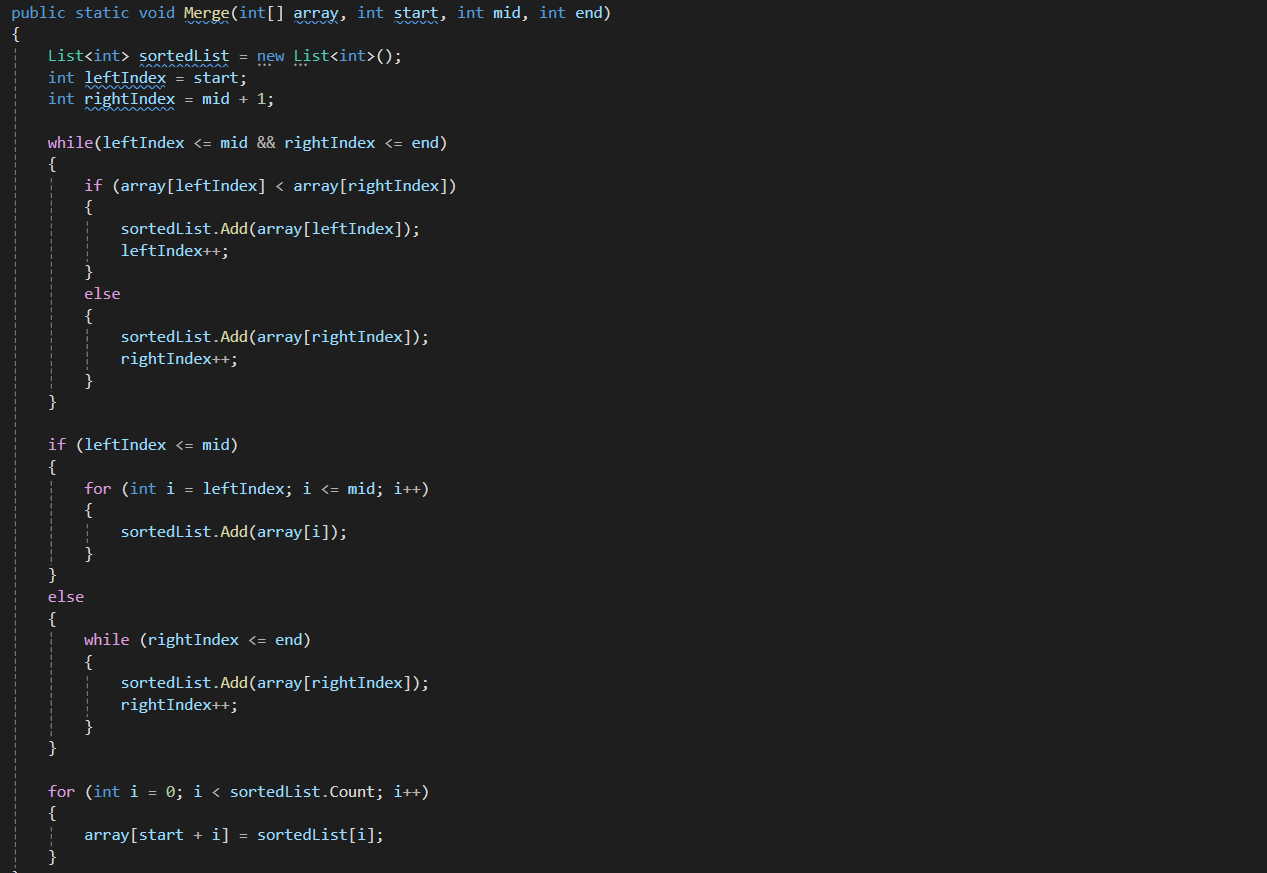
4) 병합정렬
값들을 두개씩 나누어서 정렬하고, 정렬한 값들을 또 모아서 왼,오른쪽 으로 정렬한다 이때 왼쪽 오른쪽 둘중에 값들 모두 다 정렬하여 들어갔다면 나머지
큰 값들이 자동으로 할당하여 들어가게 된다.

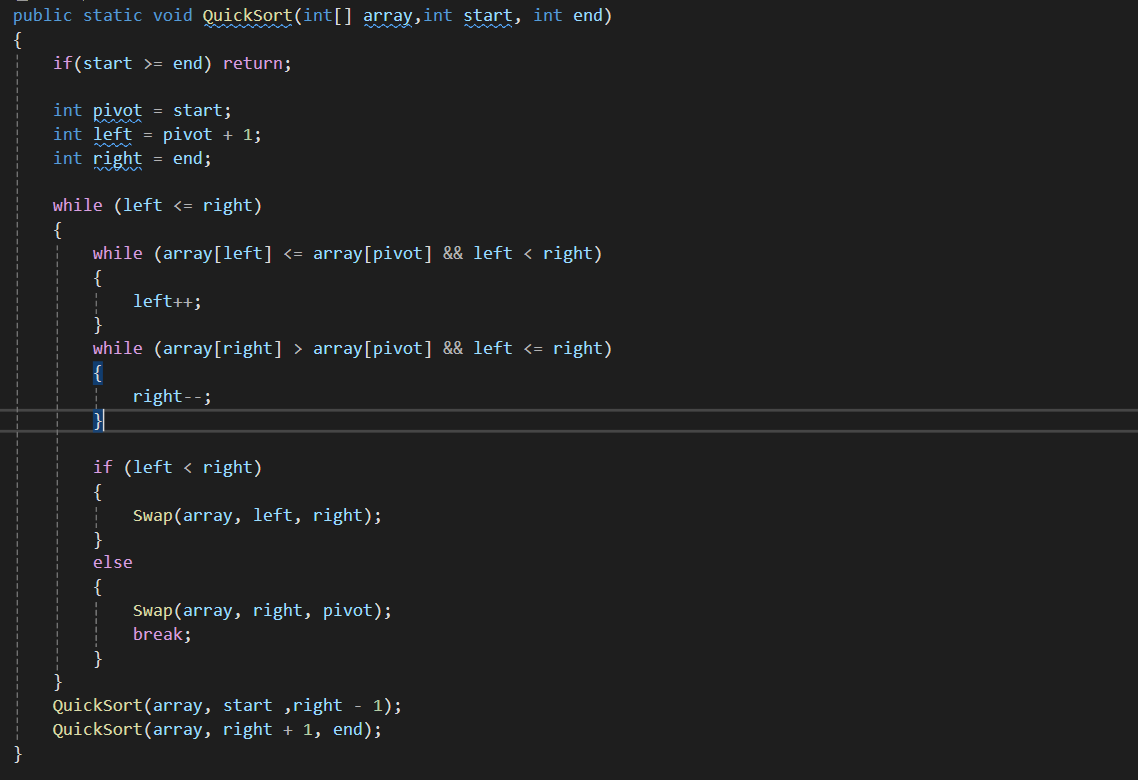
5) 퀵정렬
pivot을 선정하고 왼쪽, 오른쪽 시작점을 생성한다. 왼쪽은 +, 오른쪽은 - 방향으로 진행하면서 왼쪽은 기준값보다 클 경우 멈추고 오른쪽은 기준 값보다 작을 경우 멈춘다. 이때, 왼쪽 오른쪽 값을 바꿔준 다음 다시 pivot의 기준으로 왼쪽은 +, 오른쪽은 -방향으로 움직인다. 만약 오른쪽이 왼쪽점을 넘어갈 시 pivot과 해당 오른쪽은 바꿔주고, 이러한 방법을 반복하여 정렬시켜준다.