[algorithms]K번째 약수 풀이

N,K = list(map(int, input().split()))

if not (1<=N<=10000 and 1<=K<=N):
    print("N은 1이상 10,000 이하이며 K는 1 이상 N이하여야 합니다")
# 6의 약수 : 1,2,3,6 
# 임의로 q를 2라고 하고

# p의 약수를 리스트로 리턴하여 준다. 
def show_divisors(N,K):
    divisors = []
    for idx in range(1, N+1):
        if N%idx == 0:
            divisors.append(idx)
    print(f"dvisors : {divisors}")
    divisors_length = len(divisors)

    if divisors_length < K:
        return -1
    return divisors[K-1]

show_divisors(N,K)

6 5
dvisors : [1, 2, 3, 6]
-1

6 3
dvisors : [1, 2, 3, 6]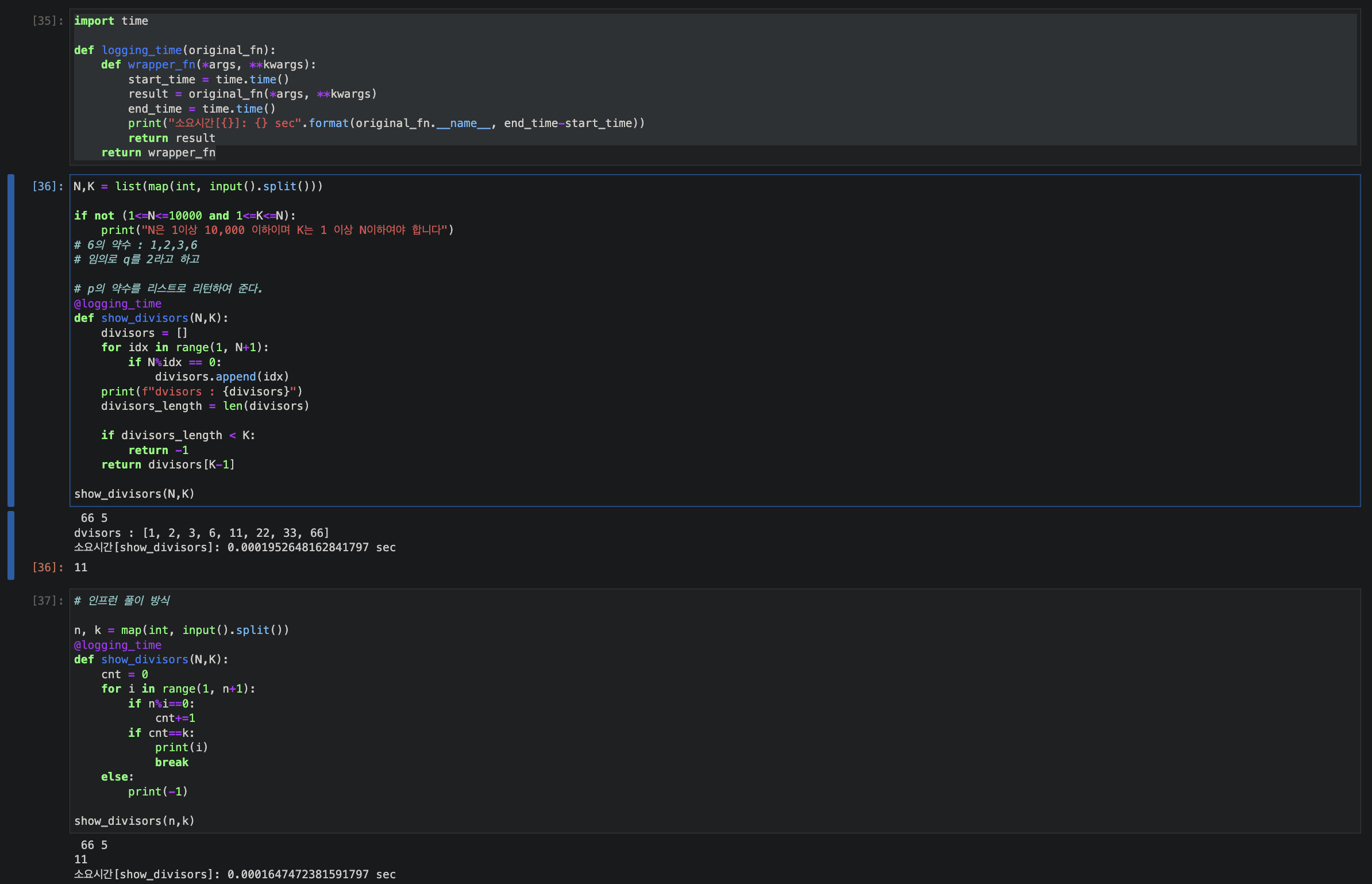

• 주의 사항 :

  • 내가 풀이한 방식에서는 divisors 리스트의 K번째 인덱스로 접근하여 K번째의 약수값이 나오지 않았다.
    그래서 인덱스에 +1을 해주어 K번째 약수가 나오도록 변경하였음.
    • 여기서 중요한 점이 K번째 인덱스 != K번째 약수는 엄연히 다르다는 점

• 결론 : 인프런 풀이 방식이 3배 이상 속도가 빠름.즉 100의 약수에서 2번째 약수를 구한다고 하면 인프런 방식은 100의 약수 모두를 알 필요 없이 1과 2까지만 연산하고 그 다음은 연산하지 않는다. 하지만 내가 처음 고안한 방식은 100의 약수를 모두 구하고 2번째 값을 구하는 방법이다.

  • 내가 만든 로직
    - 장점 : N의 약수를 메모리에서 모두 알고 있기 때문에 단발성이 아닌 여러 접근 및 풀이에서 재사용성이 있음
    - 단점 : 목적이 단순히 K번째를 알고 싶다면 K번째 이상의 약수를 구할 필요가 없으므로 리소스의 낭비일뿐
  • 인프런 방식
    - 장점 : 속도가 빠르다는 점, 불필요한 리소스 낭비가 없음
    • 단점 : 확장성 면에서 떨어질수 있음(다른 로직과의 확장성이 떨어 질것으로 생각됨)