재귀(Recursion)
하나의 함수에서 자기 자신을 다시 호출해 작업을 수행하는 알고리즘
재귀는 어떤 문제를 해결하는 과정에서 자신과 똑같지만 크기가 다른 문제를 발견하고, 이들의 관계를 파악해 문제 해결에 접근하는 방식이다.
재귀 알고리즘을 사용하면, 크고 복잡한 문제가 주어졌을 때, 문제의 크기를 결과를 얻을 수 있을정도로 점진적으로 줄인 다음, 그 결과를 이용하여 더 큰 문제를 풀어내, 처음 주어진 문제를 해결할 수 있다.
귀납적 사고
재귀 문제풀이를 위해서는 절차지향적 사고가 아닌, 귀납적 사고를 통해 문제에 접근하는 것이 필요하다.
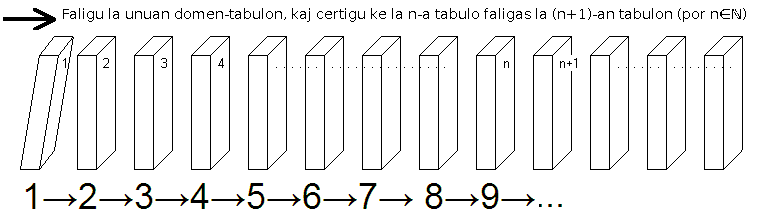
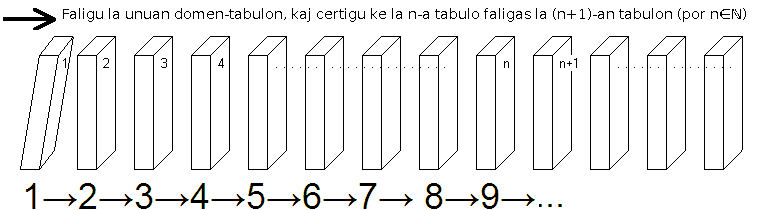(출처 위키백과)
위 사진을 보면 N번째까지 늘어진 도미노의 모습을 볼 수 있다.
1번 도미노가 쓰러지고, N번 도미노도 쓰러지면, N+1번째 도미노도 쓰러진다 => 모든 도미노는 쓰러진다는 결론에 도달
위와 같은 접근법이 귀납적 접근법이다.
재귀함수 주의할 점
Base Condition
재귀함수는 특정 입력에 대해 자기 자신을 호출하지 않고 종료해야한다.
또한 모든 입력은 Base Condition으로 수렴해야한다.
그렇지 않을 경우 스스로를 무한히 호출하다가 런타임 에러, 스택 오버플로우가 발생하게 될 것이다.
함수를 명확하게 정의하기
재귀함수를 만들때에는 함수를 명확하게 정의해야한다.
1. 함수의 인자로 어떤 값을 받을지
2. 어디까지 계산 후 넘겨줄 것인지
위 두가지를 명확히 해야한다.
PS에서의 재귀함수
재귀함수와 반복문
모든 재귀함수는 재귀 구조 없이, 단순 반복문으로만 동일 동작을 수행하는 함수를 만들 수 있다.
- 반복문을 사용하면, 메모리와 시간적 측면에서 이득이 있다. (재귀 함수를 호출하는데에 대한 비용 감소)
- 재귀함수를 사용하면 코드가 간결해진다.
따라서 반복문으로 간단히 구현이 가능하면, 반복문으로 구현하는 것이 좋고, 코드가 너무 복잡해질 것 같은 경우, 재귀함수를 사용하여 풀이하는 것이 좋다.
문제 유형
Linked List, 이진 트리, 그래프 등의 유형을 재귀 알고리즘을 통해 풀이할 수 있다.
또한 순열, 조함 같은 경우의 수를 따지는 문제도 재귀 알고리즘이 많이 활용된다.
복잡도 분석
재귀 함수가 어떻게 호출될지 알면 재귀 알고리즘의 복잡도를 구할 수 있다.
함수 내에서 재귀호출이 일어나는 횟수를 통해 시간복잡도를 구할 수 있고, 호출 스택의 최대 깊이를 통해 공간 복잡도를 구할 수 있다.
참고문헌
https://www.algodale.com/algorithms/recursion/
https://blog.encrypted.gg/943?category=773649
https://novlog.tistory.com/entry/Algorithm-%EC%9E%AC%EA%B7%80-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-Recursive-Algorithm
