먼저 이 문제를 처음 접했을 때 이동범위만 다른 최단거리 문제라고 생각되었다.
왜냐하면 주어진 이동범위로 움직이고 원하는 목표지점까지의 최단거리를 구하는 문제이기 때문이다.
이때 이동범위가 다른 부분을 어떻게 다르게 적용해야할 지 고민이 됐다.
그래서 이동 할 수 있는 범위를 배열의 인덱스로 나타내어 보면

이때 n과 m 의 조합을 정리해보면
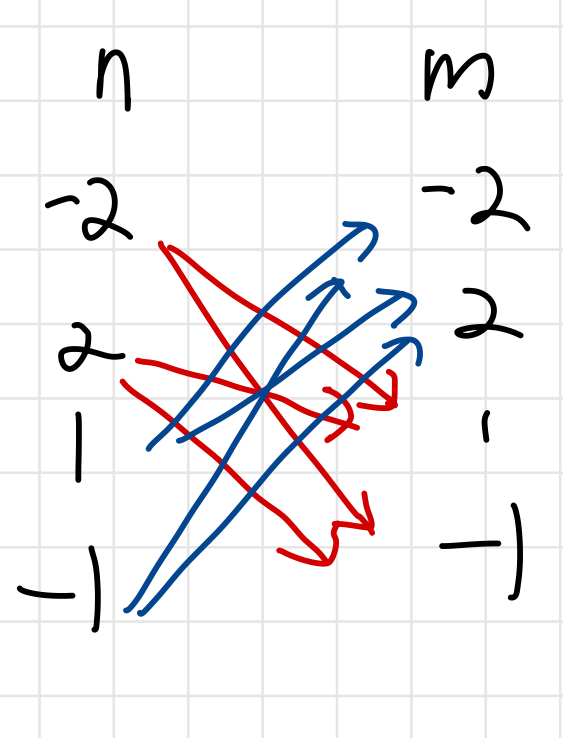
이렇게 되는 것을 알 수 있다.
그래서 n 과 m 의 절댓값이 서로 다르게 반복문을 돌 수 있도록 반복문을 두 파트로 나누어 코드를 짰다.
from collections import deque
n = int(input())
for _ in range(n):
ii = int(input())
a,b = map(int,input().split())
c,d = map(int,input().split())
graph = [[0]*ii for _ in range(ii)]
q = deque()
q.append((a,b))
dx = [-2,2,-1,1]
dy = [1,-1,-2,2]
while(q):
x,y = q.popleft()
if x == c and y == d:
break
for i in range(2):
for j in range(2):
nx = x+dx[i]
ny = y+dy[j]
if 0<=nx<ii and 0<=ny<ii and graph[nx][ny]==0:
q.append((nx,ny))
graph[nx][ny] = graph[x][y] + 1
for i in range(2,4):
for j in range(2,4):
nx = x+dx[i]
ny = y+dy[j]
if 0<=nx<ii and 0<=ny<ii and graph[nx][ny]==0:
q.append((nx,ny))
graph[nx][ny] = graph[x][y] + 1
print(graph[c][d])
이때 visted 배열은 따로 만들지 않고 방문한 곳은 +1을 하여 그래프의 값이 0인 곳만 돌도록 처리 해주었다.
