문제1. 타일 채우기 문제.
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.
이 문제는 타일 채우기 문자로, 피보나티 수열을 활용하여 해결할 수 있다.
이 문제의 해결 방법을 이해하는 데 필요한 핵심은 2×n 크기의 직사각형을 채울 때 마지막 타일이 어떻게 들어가느냐에 따라서 경우의 수가 결정된다는 점이다.
- 마지막 타일이 2×1 크기로 세로로 들어가면, 나머지 영역은 2×(n-1) 크기가 되고, 이를 채우는 방법의 수는
dp[n-1]이 된다. - 마지막 타일이 1×2 크기로 가로로 들어가면, 나머지 영역은 2×(n-2) 크기가 되고, 이를 채우는 방법의 수는
dp[n-2]이 된다.
따라서, dp[n] = dp[n-1] + dp[n-2]의 관계가 성립하게 된다.
이제 코드를 만들어보자.
먼저, dp = [0] * 1001로 1001의 크기를 가지는 리스트를 0으로 초기화 하자.
그 후에, dp[1] = 1, dp[2] = 2라는 초기 base를 설정한다.
그 후, 피보나치 수열에 관한 공식을 만든다.
dp = [0] * 1001
dp[1] = 1
dp[2] = 2
for index in range(3, 1001):
dp[index] = dp[index - 1] + dp[index - 2]
print(dp[10]) # 2x10타일 경우의 수 문제2. 파도반 수열
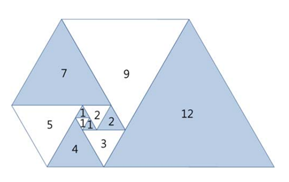
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.
N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
파도반 수열 문제는 삼각형으로 이루어진 다이아몬드 모양의 타일이 주어질 때, 그 다음에 이어지는 타일 모양을 추측하는 문제다.
문제를 잘 살펴보면, 수열은 다음과 같은 규칙을 갖는다.
P[1] = 1
P[2] = 1
P[3] = 1
P[4] = 2
P[5] = 2
...이를 통해, 다음의 규칙을 유추할 수 있다.
P[N] = P[N-1] + P[N-5]이제 이 규칙을 활용하여 코드를 작성하여 보자.
T = int(input()) # 테스트 케이스의 수
test_cases = [int(input()) for _ in range(T)] # 테스트 케이스 입력
# 우선, 100까지의 파도반 수열 값을 계산해두기 위한 리스트를 선언하고 초기값을 설정한다.
dp = [0] * 101
dp[1], dp[2], dp[3], dp[4], dp[5] = 1, 1, 1, 2, 2
for i in range(6, 101):
dp[i] = dp[i-1] + dp[i-5]
# 각 테스트 케이스에 대한 값을 출력한다.
for case in test_cases:
print(dp[case])문제3. 타일
지원이에게 2진 수열을 가르쳐 주기 위해, 지원이 아버지는 그에게 타일들을 선물해주셨다. 그리고 이 각각의 타일들은 0 또는 1이 쓰여 있는 낱장의 타일들이다.
어느 날 짓궂은 동주가 지원이의 공부를 방해하기 위해 0이 쓰여진 낱장의 타일들을 붙여서 한 쌍으로 이루어진 00 타일들을 만들었다. 결국 현재 1 하나만으로 이루어진 타일 또는 0타일을 두 개 붙인 한 쌍의 00타일들만이 남게 되었다.
그러므로 지원이는 타일로 더 이상 크기가 N인 모든 2진 수열을 만들 수 없게 되었다. 예를 들어, N=1일 때 1만 만들 수 있고, N=2일 때는 00, 11을 만들 수 있다. (01, 10은 만들 수 없게 되었다.) 또한 N=4일 때는 0011, 0000, 1001, 1100, 1111 등 총 5개의 2진 수열을 만들 수 있다.
우리의 목표는 N이 주어졌을 때 지원이가 만들 수 있는 모든 가짓수를 세는 것이다. 단 타일들은 무한히 많은 것으로 가정하자.
1개 - 1개
2개 - 2개
3개 - 1/1(2개) 0/3(1개) - 3개
4개 - 2/0(1개) 1/2(3개) 0/4(1개) - 5개
5개 - 2/1(3개) 1/3(4개) 0/5(1개) - 8개
6개 - 3/0(1개) 2/2(6개) 1/4(5개) 0/6(1개) - 13개
7개 - 3/1(4개) 2/3(10개) 1/5(6개) 0/7(1개) - 21개
피보나치 수열을 이룬다...
즉,
dp[1] = 1
dp[2] = 2
dp[n] = dp[n-1] + dp[n-2]def find_tile_combinations(n):
if n == 1:
return 1
if n == 2:
return 2
dp = [0] * (n+1)
dp[1], dp[2] = 1, 2
for i in range(3, n+1):
dp[i] = dp[i-1] + dp[i-2]
return dp[n]
n = int(input())
print(find_tile_combinations(n))이다.