System Progaramming -7- Integer Arithmetic

Shy·2023년 5월 31일

목록 보기

5/5

Shift and Rotate Instructions

Bit shifting means to move bits right and left inside an operand
x86 processors provide a particularly rich set of instructions in this area
- All affect the Overflow and Carry flags


SHL	Shift Left
SHR	Shift Right
SAL	Shift arithmetic left
SAR	Shift arithmetic right
ROL	Rotate left
ROR	Rotate Right
RCL	Rotate carry left
RCR	Rotate carry right
SHLD	Double-precision shift left
SHRD	Double-precision shift right

1.Logical Shifts and Arithmetic Shifts

Two ways to shift an operand’s bits

1.Logical shift

This shift fills the newly created bit position with zero
A byte is logically shifted one position to the right
Each bit is moved to the next lowest bit position
Note that bit 7 is assigned 0
E.g.) A single logical right shift on the binary value 11001111, producing 01100111
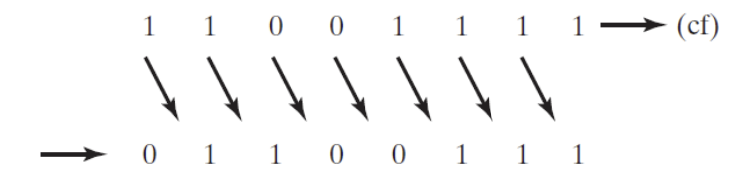
- The lowest bit is shifted into the Carry flag

2.Arithmetic shift

The newly created bit position is filled with a copy of the original number’s sign bit
E.g.) Binary 11001111 which has a 1 in the sign bit
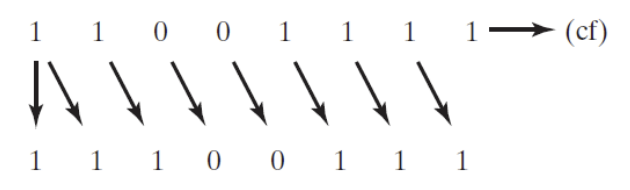
- When shifted arithmetically 1 bit to the right, it becomes 11100111

2.SHL (shift left) Instruction

Performs a logical left shift on the destination operand, filling the lowest bit with 0
The highest bit is moved to the Carry flag, and the bit that was in the Carry flag is discarded
E.g.) If you shift 11001111 left by 1 bit, it becomes 10011110
Instruction format
```
SHL destination, count
```
```
SHL reg, imm8
SHL mem, imm8
SHL reg, CL
SHL mem, CL
```
- x86 processors permit imm8 to be any integer between 0 and 255
- Alternatively, the CL register can contain a shift count
Example
```
mov bl, 8Fh		; BL = 10001111b
shl bl, l			; CF - 1, BL - 00011110b
```
- BL is shifted once to the left
- The highest bit is copied into the Carry flag and the lowest bit position is assigned zero
```
mov al,10000000b
shl al,2					; CF = 0, AL - 00000000b
```
- When a value is shifted leftward multiple times, the CF contains the last bit to be shifted out of the MSB
- Bit 7 does not end up in the CF because it is replaced by bit 6 (a zero)
- Similarly, when a value is shifted rightward multiple times, the CF contains the last bit to be shifted out of the LSB
Bitwise Multiplication
- Bitwise multiplication is performed when you shift a number’s bits in a leftward direction (toward the MSB)
  - E.g.) SHL can perform multiplication by powers of 2
- Shifting any operand left by 𝑛𝑛 bits multiplies the operand by 2^𝑛
  - E.g.) Shifting the integer 5 left by 1 bit yields the product of 5 × (2^1) = 10
  
  - E.g.) If binary 00001010 (decimal 10) is shifted left by two bits, the result is the same as multiplying 10 by 2^2
```
```
  mov dl,10			; before 00001010
  shl dl,2			; after 00101000
```
```

3.SHR (shift right) Instruction

performs a logical right shift on the destination operand, replacing the highest bit with a 0
The lowest bit is copied into the Carry flag, and the bit that was previously in the Carry flag is lost
SHR uses the same instruction formats as SHL
Examples
```
mov al,0D0h			; AL = 11010000b
shr al,1				; AL = 01101000b, CF = 0 
```
- The 0 from the lowest bit in AL is copied into the CF, and the highest bit in AL is filled with a zero
```
mov al,00000010b
shr al,2				; AL = 00000000b, CF = 1
```
- In a multiple shift operation, the last bit to be shifted out of position 0 (the LSB) ends up in the Carry flag
Bitwise Division
- Bitwise division is accomplished when you shift a number’s bits in a rightward direction (toward the LSB)
- Shifting an unsigned integer right by 𝑛𝑛 bits divides the operand by 2^𝑛
- E.g.) 32 is divided by 2^1, producing 16
- E.g.) 32 is divided by 2^3
```
mov al,01000000b			; AL = 64
shr al,3					; divide by 8, AL = 00001000b
```
- Division of signed numbers by shifting is accomplished using the SAR instruction because it preserves the number’s sign bit

4.SAL (shift arithmetic left) and SAR (shift arithmetic right) Instructions

The SAL instruction works the same as the SHL instruction
- For each shift count, SAL shifts each bit in the destination operand to the next highest bit position
- The lowest bit is assigned 0
- The highest bit is moved to the Carry flag, and the bit that was in the Carry flag is discarded
- E.g.) If you shift binary 11001111 to the left by one bit, it becomes 10011110
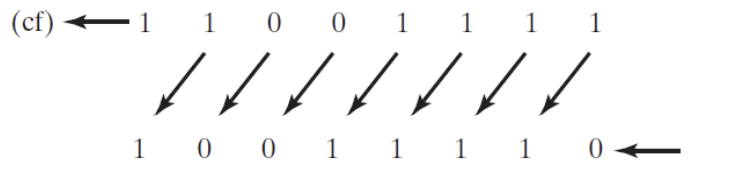
The SAR instruction performs a right arithmetic shift on its destination operand
Example
- This example shows how SAR duplicates the sign bit
- AL is negative before and after it is shifted to the right
```
mov al, 0F0h			; AL = 11110000 (-16)
sar al, 1				; AL = 11111000 (-8), CF = 0
```
Signed Division
- You can divide a signed operand by a power of 2, using the SAR instruction
- In the following example, −128 is divided by 23. The quotient is −16
```
mov dl,-128			; DL = 10000000b
sar dl,3				; DL = 11110000b
```
Sign-Extend AX into EAX
- Suppose AX contains a signed integer and you want to extend its sign into EAX
- First shift EAX 16 bits to the left, then shift it arithmetically 16 bits to the right
```
mov ax,128			; EAX = ????FF80h
shl eax,16			; EAX = FF800000h
sar eax,16			; EAX = FFFFFF80h
```

5.ROL (rotate left) Instruction

Bitwise rotation occurs when you move the bits in a circular fashion
- In some versions, the bit leaving one end of the number is immediately copied into the other end
- Another type of rotation uses the Carry flag as an intermediate point for shifted bits
The ROL instruction shifts each bit to the left
The highest bit is copied into the Carry flag and the lowest bit position
Bit rotation does not lose bits
- A bit rotated off one end of a number appears again at the other end
The following example shows how the high bit is copied into both the Carry flag and bit position 0

mov al,40h		; AL = 01000000b,
rol al,1		; AL = 10000000b, CF = 0
rol al,1		; AL - 00000001b, CF = 1
rol al,1		; AL - 00000010b, CF = 0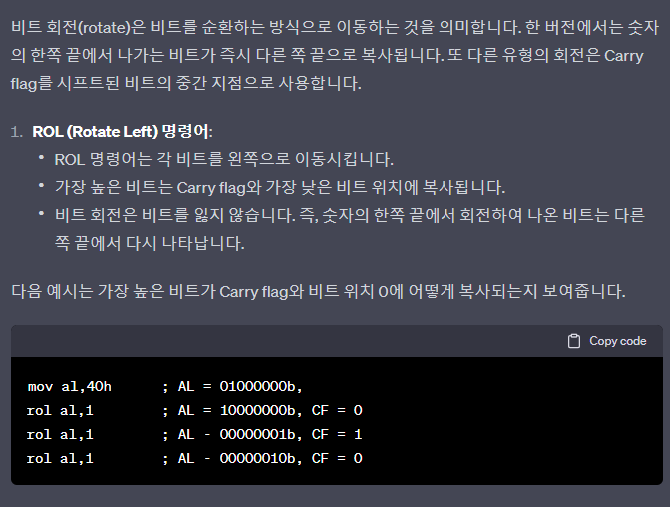

6.ROR (rotate right) Instruction

The ROR instruction shifts each bit to the right and copies the lowest bit into the Carry flag and thehighest bit position
Example

mov al,01h			; AL = 00000001b
ror al,1			; AL = 10000000b, CF = 1
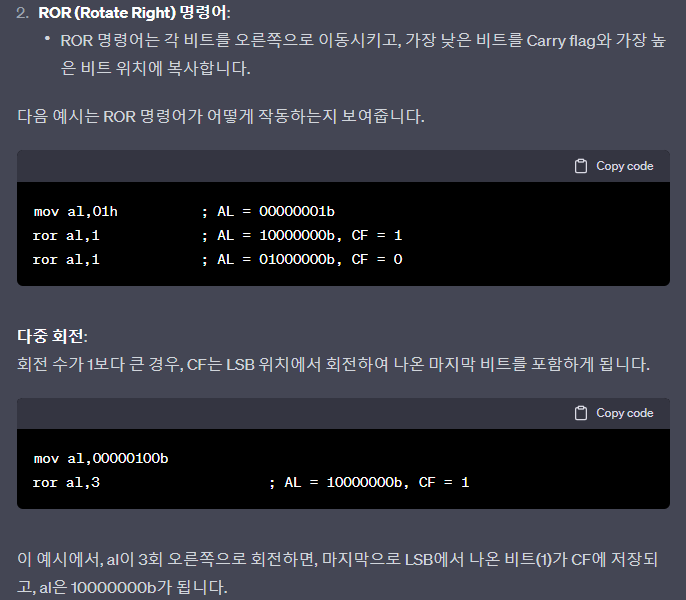
ror al,1			; AL = 01000000b, CF = 0

Multiple Rotations
- When using a rotation count greater than 1, the CF contains the last bit rotated out of the LSB position
```
mov al,00000100b
ror al,3					; AL = 10000000b, CF = 1
```

7.RCL (rotate carry left) and RCR (rotate carry right) Instructions

RCL shifts each bit to the left, copies the CF to the LSB, and copies the MSB into the CF
If we imagine the CF as an extra bit added to the high end of the operand, RCL looks like a rotate left operation
Example
```
clc					; CF = 0
mov bl,88h				; CF,BL=0 10001000b
rcl bl,1				; CF,BL=1 00010000b
rcl bl,1				; CF,BL=0 00100001b
```
- The CLC instruction clears the CF
- The first RCL instruction moves the high bit of BL into the CF and shifts the other bits left
- The second RCL instruction moves the CF into the lowest bit position and shifts the other bits left
Recover a Bit from the Carry Flag
- RCL can recover a bit that was previously shifted into the Carry flag
- The following example checks the lowest bit of testval by shifting its lowest bit into the CF
  - If the lowest bit of testval is 1, a jump is taken
  - If the lowest bit is 0, RCL restores the number to its original value
RCR Instruction
- The RCR instruction shifts each bit to the right, copies the CF into the MSB, and copies the LSB into the CF
- The following code example uses STC to set the CF; then, it performs a rotate carry right operation on the AH register
```
stc				; CF = 1
mov ah,10h			; AH, CF = 00010000 1
rcr ah,1			; AH, CF = 10001000 0
```

8.Signed Overflow

The Overflow flag is set if the act of shifting or rotating a signed integer by one bit position
generates a value outside the signed integer range of the destination operand
- To put it another way, the number’s sign is reversed
The value of the Overflow flag is undefined when the shift or rotation count is greater than 1
Examples
- A positive integer (+127) stored in an 8-bit register becomes negative (−2) when rotated left
```
mov al,+127			; AL = 01111111b		
rol al,1				; OF = 1, AL = 11111110b
```
- Similarly, when – 128 is shifted one position to the right, the Overflow flag is set
- The result in AL (+64) has the opposite sign
```
mov al,-128			; AL = 10000000b
shr al,1				; OF = 1, AL = 01000000b
```

9.SHLD (shift left double) / SHRD (shift right double) Instructions

The SHLD instruction
```
SHLD dest, source, count
```
- The SHLD shifts a destination operand a given number of bits to the left
- The bit positions opened up by the shift are filled by the MSBs of the source operand
- The source operand is not affected, but the Sign, Zero, Auxiliary, Parity, and Carry flags are affected
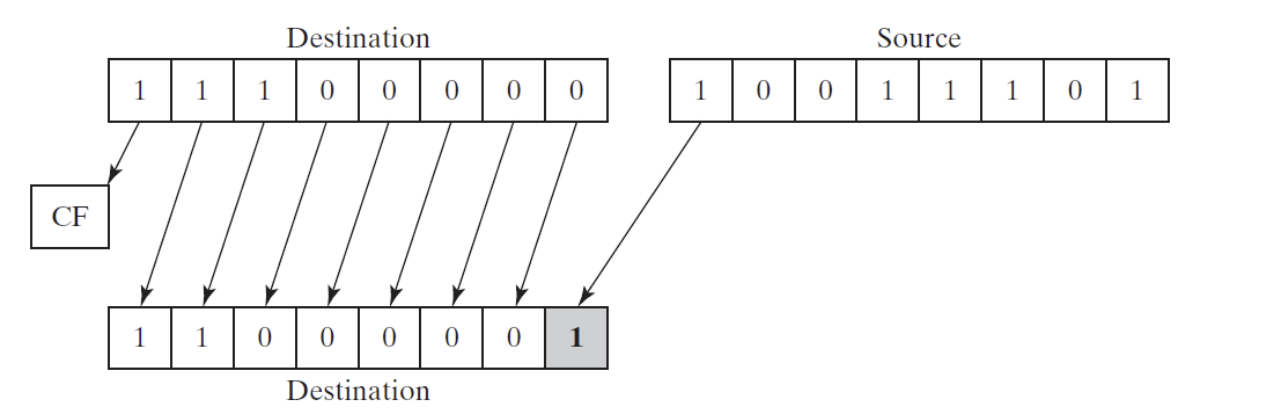
  - The illustration shows the execution of SHLD with a shift count of 1
  - The highest bit of the source operand is copied into the lowest bit of the destination operand
  - All the destination operand bits are shifted left
The SHRD instruction
```
SHRD dest, source, count
```
- The SHRD shifts a destination operand a given number of bits to the right
- The bit positions opened up by the shift are filled by the LSBs of the source operand
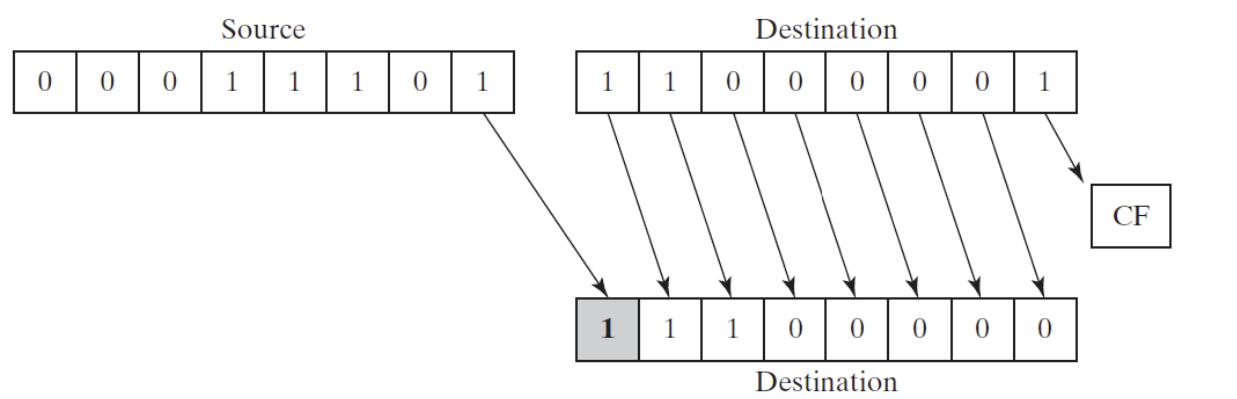
  - The illustration shows the execution of SHRD with a shift count of 1
Instruction formats
- The destination operand can be a register or memory operand
- The source operand must be a register
- The count operand can be the CL register or an 8-bit immediate operand
```
SHLD reg16,reg16,CL/imm8
SHLD mem16,reg16,CL/imm8
SHLD reg32,reg32,CL/imm8
SHLD mem32,reg32,CL/imm8
```

Example 1
- The following statements shift wval to the left 4 bits and insert the high 4 bits of AX into the low 4 bit positions of wval
```
.data
wval WORD 0BA6h
.code
mov ax,0AC36h
shld wval,ax,4		; wval = BA6Ah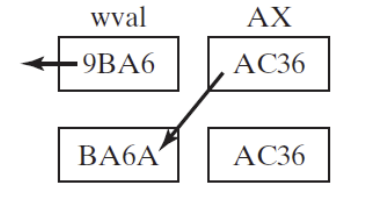
```
Example 2
- AX is shifted to the right 4 bits, and the low 4 bits of DX are shifted into the high 4 positions of AX
```
mov ax,234Bh
mov dx,7654h
shrd ax,dx,4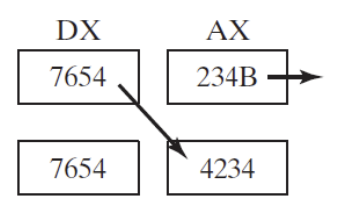
```
Applications
- SHLD and SHRD can be used to manipulate bit-mapped images, when groups of bits must be shifted left and right to reposition images on the screen
- Another potential application is data encryption, in which the encryption algorithm involves the shifting of bits
- Finally, the two instructions can be used when performing fast multiplication and division with very long integers
- E.g.) shifting an array of doublewords to the right by 4 bits

.data
array DWORD 648B2165h, 8C943A29h, 6DFA4B86h, 91F76C04h, 8BAF9857h
.code
		mov bl,4						;shift count
  		mov esi,OFFSET array			; offset of the array
  		mov ecx,(LENGTHOF array) - 1	; number of array elements
  
L1: 	push ecx						; save loop counter
		mov eax,[esi + TYPE DWORD]
        mov cl,bl						; shift count
        shrd [esi],eax,cl				; shift EAX into high bits of [ESI]
        add esi,TYPE DWORD				; point to next doubleword pair
        pop ecx							; restore loop counter
        loop L1
        
        shr DWORD PTR [esi],COUNT		; shift ther last doubleword

Shift and Rotate Applications

1.Shifting Multiple Doublewords

You can shift an extended-precision integer that has been divided into an array of bytes, words, or doublewords
A common way to store the integer (little-endian order)
- Place the low-order byte at the array’s starting address
- Then, working your way up from that byte to the high-order byte, store each in the next sequential memory location
- Instead of storing the array as a series of bytes, you could store it as a series of words or doublewords
- If you did so, the individual bytes would still be in little-endian order, because x86 machines store words and doublewords in little-endian order
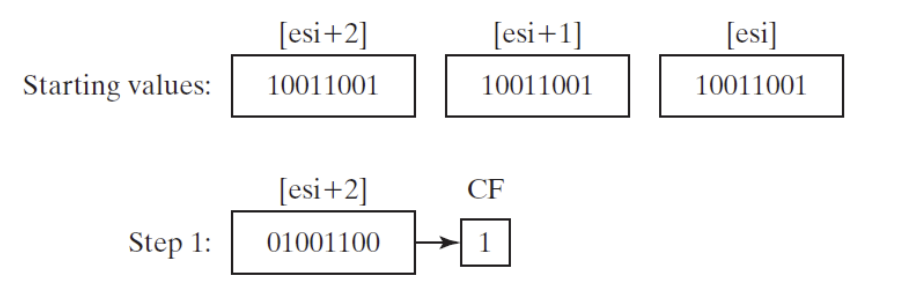
How to shift an array of bytes 1 bit to the right
Step 1: Shift the highest byte at [ESI+2] to the right, automatically copying its lowest bit into the CF
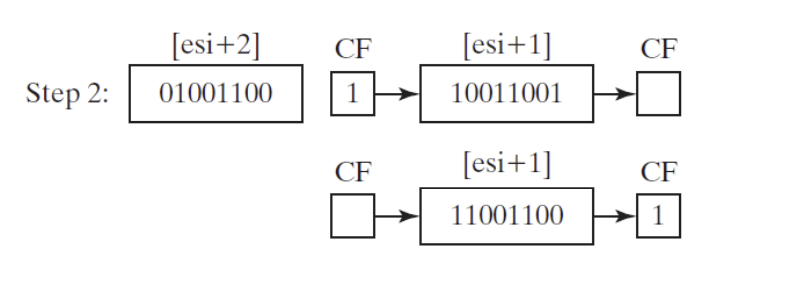
Step 2: Rotate the value at [ESI+1] to the right, filling the highest bit with the value of the CF, and shifting the lowest bit into the CF
Step 3: Rotate the value at [ESI] to the right, filling the highest bit with the value of the CF, and shifting the lowest bit into the CF
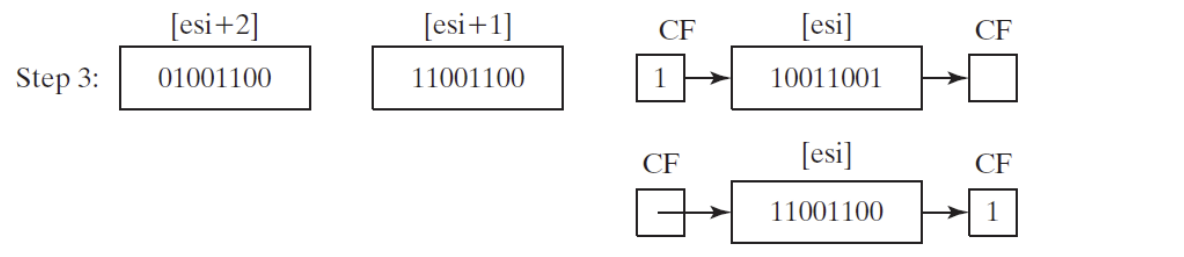
After Step 3 is complete, all bits have been shifted 1 position to the right

Assembly language code

.data
ArraySize = 3
array BYTE ArraySize DUP(99h)	; 1001 pattern in each nybble
.code
main PROC
	mov esi,0
    shr array[esi+2],1			; high byte
    rcr array[esi+1],1			; middle byte, include Carry flag
    rcr array[esi],1			; low byte, include Carry flag

Although this example only shifts 3 bytes, the example could easily be modified to shift an array of words or doublewords
Using a loop, you could shift an array of arbitrary size

2.Binary Multiplication

Sometimes programmers squeeze every performance advantage they can into integer multiplication by using bit shifting rather than the MUL instruction
The SHL instruction performs unsigned multiplication when the multiplier is a power of 2
- Shifting an unsigned integer 𝑛𝑛 bits to the left multiplies it by 2𝑛𝑛
- Any other multiplier can be expressed as the sum of powers of 2^n
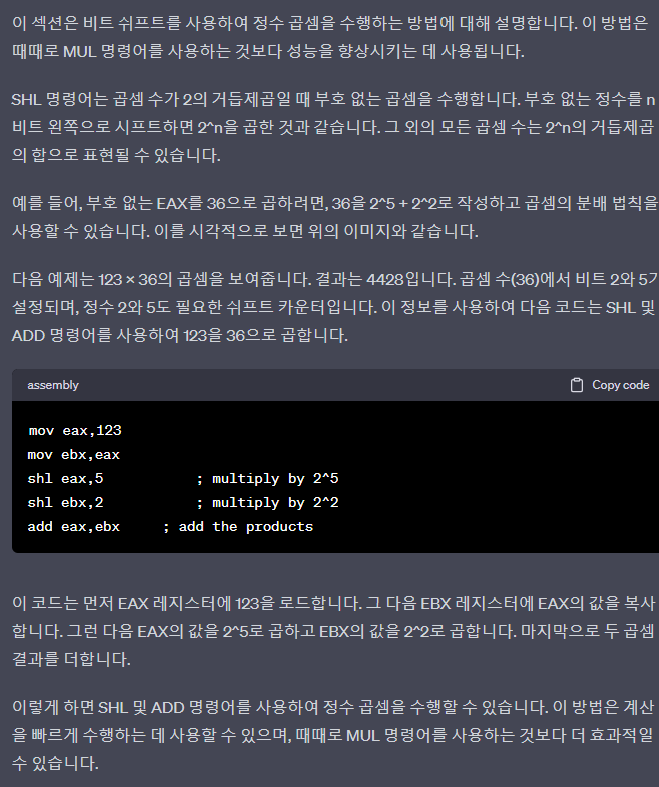
- E.g.) To multiply unsigned EAX by 36, we can write 36 as 2^5 + 2^2 and use the distributive property of multiplication
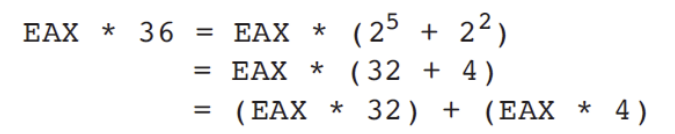
The following example shows the multiplication 123 × 36, producing 4428
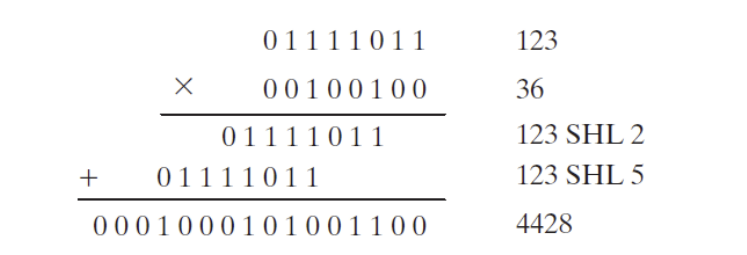
- Bits 2 and 5 are set in the multiplier (36), and the integers 2 and 5 are also the required shift counters
- Using this information, the following code multiplies 123 by 36, using SHL and ADD instructions
```
mov eax,123
mov ebx,eax
shl eax,5			; multiply by 2^5
shl ebx,2			; multiply by 2^2
add eax,ebx		; add the products
```

3. Displaying Binary Bits

Converting a binary integer to an ASCII binary string, allowing the latter to be displayed
- The SHL instruction is useful in this regard because it copies the highest bit of an operand into the CF each time the operand is shifted left
- The following procedure is a simple implementation

;------------------------------------------------------
;BitToAsc Proc
;
;Converts 32-bit binary integer to ASCⅡ binary
;Receives: EAX = binary integer, ESI points to bufer
;Returns: buffer filled with ASCⅡ binary digits
;------------------------------------------------------
	push ecx
	push esi
	mov ecx, 32					;number of bits in EAX

L1;	shl eax,1					; shift high bit into Carry flag
	mov BYTE PTR [esi], '0'		;choose 0 as default digit
    jnc L2						; if no Carry, jump to L2
    mov BYTE PTR [esi], '1		; else move 1 to buffer

L2: inc esi						; next buffer position
	loop L1						; shift another bit to left
    pop esi
    pop ecx
    ret

BinToAsc ENDP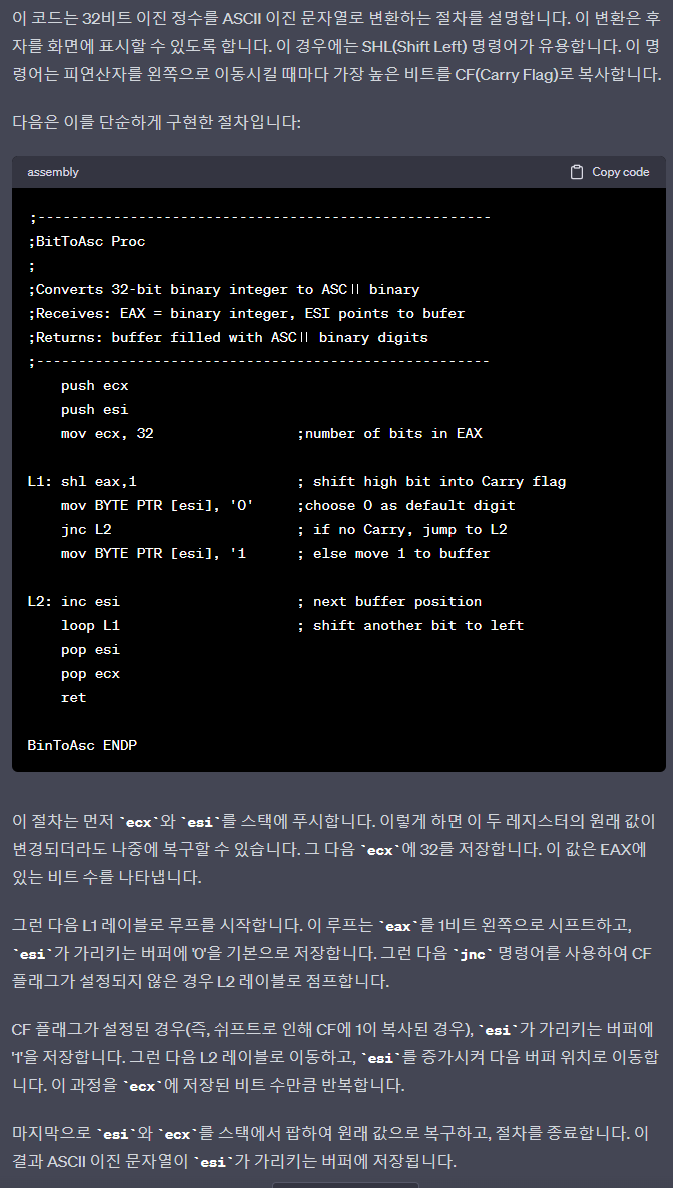

4.Extracting File Date Fields

When storage space is at a premium, system-level software often packs multiple data fields into a single integer
To uncover this data, applications often need to extract sequences of bits called bit strings
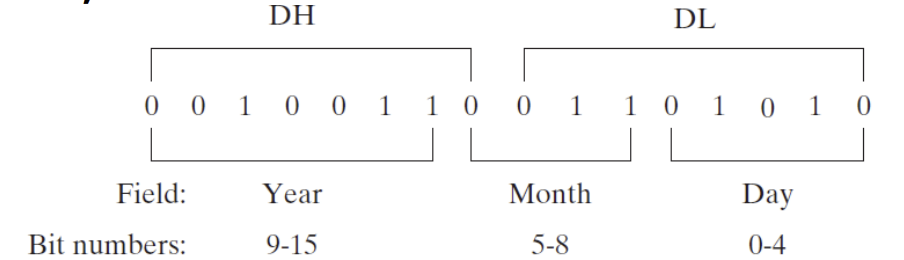
E.g.) in real-address mode, MS-DOS function 57h returns the date stamp of a file in DX
- The date stamp shows the date on which the file was last modified
- Bits 0 through 4 represent a day number between 1 and 31
- Bits 5 through 8 are the month number
- Bits 9 through 15 hold the year number
- If a file was last modified on March 10, 1999, the file’s date stamp would appear as follows in the DX register (the year number is relative to 1980)
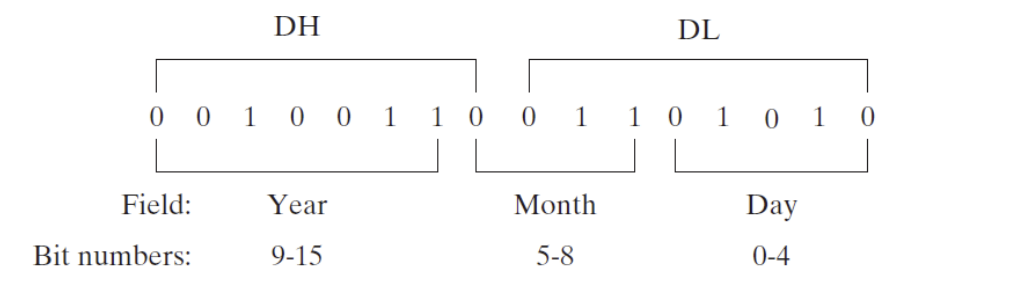
E.g.) in real-address mode, MS-DOS function 57h returns the date stamp of a file in DX

To extract a single bit string, shift its bits into the lowest part of a register and clear the irrelevant bits

Extracting the day number field

mov al,dl				; make a copy of DL
and al,00011111b		; clear bits 5-7
mov day,al				;save in day

Extracting the month number field

mov ax,dx				; make a copy of DX
shr ax,5				; shift right 5 bits
and al,00001111b		; clear bits 4-7
mov month,al			; save in month

Extracting the year number field

mov al,dh				; make a copy of DH
shr al,1				; shift tight one position
mov ah,0				; clear AH to zeros
add ax,1980			; yeat is relative to 1980
mov year,ax			; save in year

Multiplication and Division Instructions

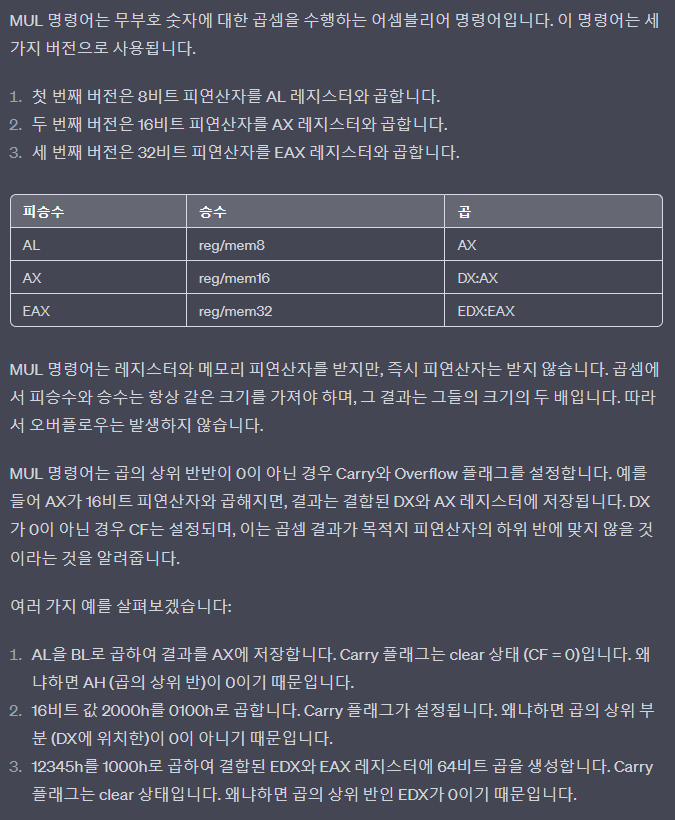
1.MUL (unsigned multiply) Instruction

The MUL instruction comes in three versions
- The 1st version multiplies an 8-bit operand by the AL register
- The 2nd version multiplies a 16-bit operand by the AX register
- The 3rd version multiplies a 32-bit operand by the EAX register

Multiplicand	Multiplier	Product
AL	reg/mem8	AX
AX	reg/mem16	DX:AX
EAX	reg/mem32	EDX:EAX

The three formats accept register and memory operands, but not immediate operands

MUL reg/mem8
MUL reg/mem16
MUL reg/mem32

The multiplier and multiplicand must always be the same size, and the product is twice their size
- So, overflow cannot occur
MUL sets the Carry and Overflow flags if the upper half of the product is not equal to zero
- E.g.) When AX is multiplied by a 16-bit operand, the product is stored in the combined DX and AX registers
  - The CF is set if DX is not equal to zero, which lets us know that the product will not fit into the lower half of the implied destination operand
MUL Examples
- Multiplying AL by BL, storing the product in AX
  - The Carry flag is clear (CF = 0) because AH (the upper half of the product) equals zero
```
mov al,5h
mov bl,10h
mul bl			; AX = 0050h, CF = 0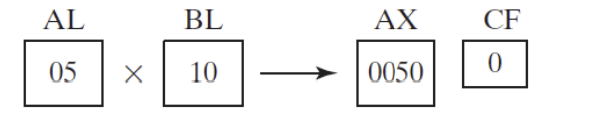
```
- Multiplying the 16-bit value 2000h by 0100h
  - The CF is set because the upper part of the product (located in DX) is not equal to zero
```
.data
val1 WORD 2000h
val2 WORD 0100h
.code
mov ax,val1			; AX = 2000h
mul val2			; DX:AX = 00200000h, CF = 1
```
- Multiplying 12345h by 1000h, producing a 64-bit product in the combined EDX and EAX registers
  - The Carry flag is clear because the upper half of the product in EDX equals zero
```
mov eax,12345h
mov ebx,1000h
mul ebx					; EDX:EAX = 0000000012345000h, CF = 0
```

2.IMUL(signed multiply) Instruction

The IMUL instruction performs signed integer multiplication
Unlike the MUL instruction, IMUL preserves the sign of the product
- It sign-extends the highest bit of the lower half of the product into the upper bits of the product
The x86 instruction set supports three formats for the IMUL instruction
- One operand, two operands, and three operands
- In the one-operand format, the multiplier and multiplicand are the same size and the product is twice their size
Single-Operand Formats
- The one-operand formats stroe the product in AX, DX:AX, or EDX:EAX
```
IMUL reg/mem8		; AX = AL * reg/mem8
IMUL reg/mem16		; DX:AX = AX * reg/mem16
IMUL reg/mem32		; EDX:EAX = EAX * reg/mem32
```
- The storage size of the product makes overflow impossible
- The CF and OF are set if the upper half of the product is not a sign extension of the lower half
  - You can use this information to decide whether to ignore the upper half of the product
Two-Operand Formats
- The two-operand version stores the product in the first operand, which must be a register
- The second operand (the multiplier) can be a register, a memory operand, or an immediate value
```
IMUL reg16,reg/mem16		IMUL reg32,reg/mem32
IMUL reg16,imm8				IMUL reg32,imm8
IMUL reg16,imm16			IMUL reg32,imm32
```
- The two-operand formats truncate the product to the length of the destination
- If significant digits are lost, the OF and CF are set
  - Be sure to check one of these flags after performing an IMUL operation with two operands
Three-Operand Formats
- The three-operand formats store the product in the first operand
- The second operand can be a register or memory operand, which is multiplied by the third operand, an immediate value
```
IMUL reg16,reg/mem16,imm8		IMUL reg32,reg/mem32,imm8
IMUL reg16,reg/mem16,imm16		IMUL reg32,reg/mem32,imm32
```
- If significant digits are lost when IMUL executes, the OF and CF are set
  - Be sure to check one of these flags after performing an IMUL operation with three operands
Unsigned Multiplication
- The two-operand and three-operand IMUL formats may also be used for unsigned multiplication because the lower half of the product is the same for signed and unsigned numbers
- A small disadvantage
  - The Carry and Overflow flags will not indicate whether the upper half of the product equals zero

IMUL Examples

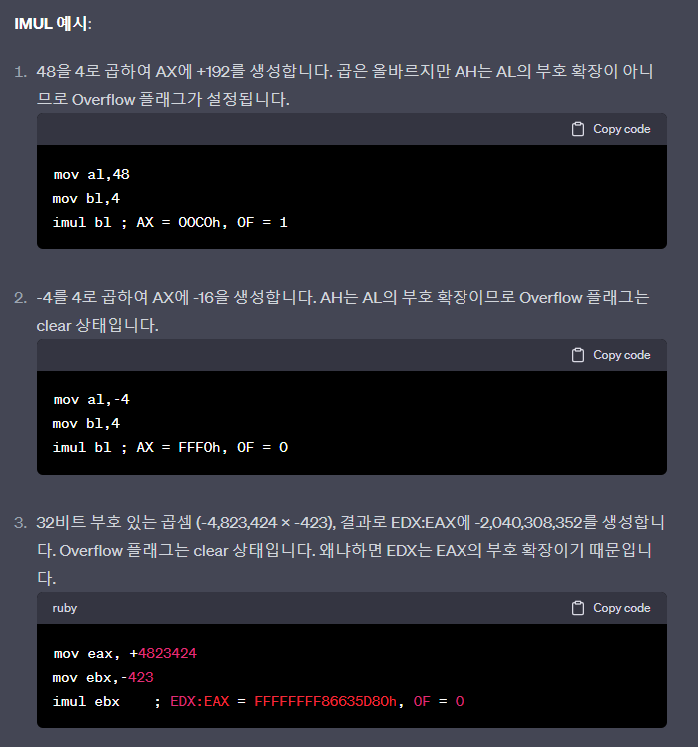
Multiplying 48 by 4, producing +192 in AX
- Although the product is correct, AH is not a sign extension of AL, so the Overflow flag is set
```
mov al,48
mov bl,4
imul bl				; AX = 00C0h, OF = 1
```
Multiplying −4 by 4, producing −16 in AX
- AH is a sign extension of AL, so the Overflow flag is clear
```
mov al,-4
mov bl,4
imul bl				; AX = FFF0h, OF = 0
```
32-bit signed multiplication (−4,823,424 × −423), producing −2,040,308,352 in EDX:EAX
- The Overflow flag is clear because EDX is a sign extension of EAX
```
mov eax, +4823424
mov ebx,-423
imul ebx				; EDX:EAX = FFFFFFFF86635D80h, OF = 0
```
Two-operand formats

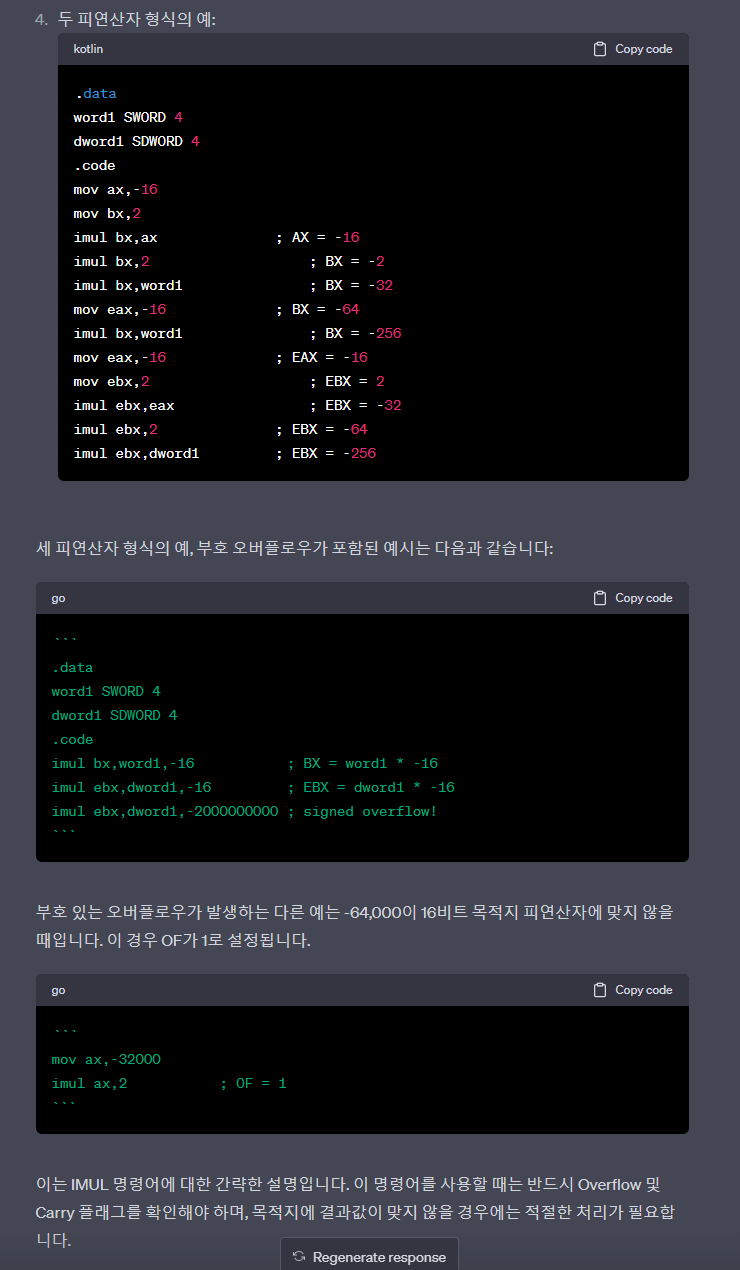
.data
word1 SWORD 4
dword1 SDWORD 4
.code
mov ax,-16
mov bx,2
imul bx,ax				; AX = -16
imul bx,2					; BX = -2
imul bx,word1				; BX = -32
mov eax,-16				; BX = -64
imul bx,word1				; BX = -256
mov eax,-16				; EAX = -16
mov ebx,2					; EBX = 2
imul ebx,eax				; EBX = -32
imul ebx,2				; EBX = -64
imul ebx,dword1			; EBX = -256

The two-operand and three-operand IMUL instructions use a destination operand that is the same size as the multiplier
- Therefore, it is possible for signed overflow to occur
- Always check the OF after executing these types of IMUL instructions
The following two-operand instructions demonstrate signed overflow because −64,000 cannot fit within the 16-bit destination operand

mov ax,-32000
imul ax,2			; OF = 1

The following instructions demonstrate three-operand formats, including an example of signed overflow

.data
word1 SWORD 4
dword1 SDWORD 4
.code
imul bx,word1,-16			; BX = word1 * -16
imul ebx,dword1,-16			; EBX = dword1 * -16
imul ebx,dword1,-2000000000	; signed overflow!

3. Measuring Program Execution Times

.data
startTime DWORD ?
procTime1 DWORD ?
procTime2 DWORD ?
.code
call GetMseconds			; get start time
mov startTime,eax
.
call FirstProcedureToTest
.
call GetMseconds			; get stop time
sub eax,startTime			; calcilate the elapsed time
mov procTIme1,eax			; save the elapsed time
.
.
.
get GetMseconds				; get start time
mov startTime,eax
.
call SecondProcedureToTest
.
call GetMseconds			; get stop time
sub eax,startTime			; calculate the elapsed time
mov procTime2,eax			; save the elapsed time

Comparing MUL and IMUL to Bit Shifting
- In older x86 processors, there was a significant difference in performance between multiplication by bit shifting vs. multiplication using the MUL and IMUL instructions

mult_by_shifting PROC
; Multiplies EAX by 36 using SHL, LOOP_COUNT times.
;
	mov ecx, LOOP_COUNT
L1: push 	eax					; save original EAX
	mov		ebx, eax
    shl		eax, 5
    shl		ebx, 2
    add		eax, ebx
    pop		eax
    loop	L1
    ret
mult_by_shifting ENDP

mult_by_MUL PROC
; Multiplies EAX by 36 using MUL, LOOP_COUNT times.
;
	mov 	ecx, LOOP_COUNT
L1:	push	eax					; save original EAX
	mul		ebx
    pop		eax
    loop	L1
    ret
mult_by_MUL ENDP
.data
LOOP_COUNT = 0FFFFFFFFh
.data
intval DWORD 5
startTime DWORD ?
.code
call		GetMseconds			; get start time
mov			startTime,eax
mov			eax,intval
call		mult_by_shifting
call		GetMseconds			; get stop time
sub			eax, startTime
call		WriteDec			; display elapsed time

The resulting timings on a legacy 4-GHz Pentium 4 showed that the SHL approach executed in 6.078 seconds and the MUL approach executed in 20.718 seconds
However, when running the same program on a more recent processor, the timings of both function calls were exactly the same
This example shows that Intel has managed to greatly optimize the MUL and IMUL instructions in recent processors

4. DIV (unsigned divide) Instruction

DIV instruction performs 8-bit, 16-bit, and 32-bit unsigned integer division
The single register or memory operand is the divisor

DIV reg/mem8
DIV reg/mem16
DIV reg/mem32

Dividend	Divisor	Quotient	Remainder
AX	reg/mem8	AL	AH
DX:AX	reg/mem16	AX	DX
EDX:EAX	reg/mem32	EAX	EDX

DIV Examples

8-bit unsigned division (83h/2), producing a quotient of 41h and a remainder of 1

mov ax, 0083h				; dividend
mov bl,2					; divisor
div bl					; AL = 41h, AH = 01h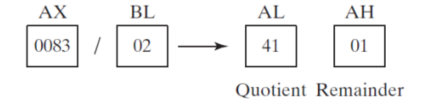

16-bit unsigned division (8003h/100h), producing a quotient of 80h and a remainder of 3
- DX contains the high part of the dividend, so it must be cleared before the DIV instruction executes
```
mov dx, 0				; clear dividend, high
mov ax, 8003h			; dividend, low
mov cx, 100h			; divisor
div cx					; AX = 0080h, DX = 0003h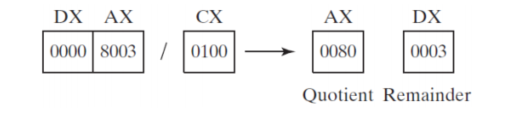
```

32-bit unsigned division using a memory operand as the divisor

.data
dividend QWORD 0000000800300020h
divisor DWORD 00000100h
.code
mov edx,DWORD PTR dividend + 4 	; high doubleword
mov eax,DWORD PTR dividend		; low doubleword
div divisor						; EAX = 08003000h, EDX = 00000020h

5.Signed Integer Division

Signed integer division is nearly identical to unsigned division, with one important difference:
- The dividend must be sign-extended before the division takes place
Sign Extension Instructions (CBW, CWD, CDQ)
- The CBW (convert byte to word) extends the sign bit of AL into AH, preserving the number’s sign
- The CWD (convert word to doubleword) instruction extends the sign bit of AX into DX
- The CDQ (convert doubleword to quadword) instruction extends the sign bit of EAX into EDX

.data
byteVal SBYTE -101		; 9Bh
.code
mov  al, byteVal		; AL = 9Bh
cbw
---------------------------------------
.data
wordVal SWORD -101		; FF9Bh
.code
mov ax, wordVal			; AX = FF9Bh
cwd						; DX:AX = FFFFFF9Bh
---------------------------------------
.data
dwordVal SDWORD -101 	; FFFFFF9Bh
.code
mov eax, dwordVal
cdq						; EDX:EAX = FFFFFFFFFFFFFF9Bh

The IDIV (signed divide) Instruction
- The IDIV instruction performs signed integer division, using the same operands as DIV
- Before executing 8-bit division, the dividend (AX) must be completely sign-extended
- The remainder always has the same sign as the dividend
- Example 1
  - The following instructions divide -48 by 5
  - After IDIV executes, the quotient in AL is -9 and the remainder in AH is -3

.data
byteVal SBYTE -48			; D0 hexadecimal
.code
mov al,byteVal				; lower half of dividend
cbw							; extend AL into AH
bov bl, +5					; divisor
idiv bl						; AL = -9, AH = -3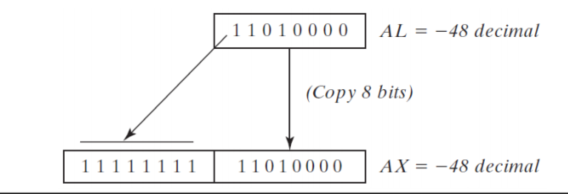

The IDIV (signed divide) Instruction

Example 2

16-Bit division requires AX to be sign-extended into DX
The next example divides -5000 by 256

.data
wordVal SWORD -5000
.code
mov ax,wordVal				; dividend, low
cwd							; extend AX into DX
mov bx, +256				; divisor
idiv bx						; quotient AX = -19, rem DX = -136

Example 3
- 32-Bit division requires EAX to be sign-extended into EDX
- The next example divides 50,000 by -256

```
.data
dwordVal SDWORD +50000
.code
mov eax,dwordVal			; dividend, low
cdq							; extend EAX into EDX
mov ebx, -256				; divisor
idiv ebx					; quotient EAX = 195, rem EDX = +80
```

All arithmetic status flag values are undefined after executing DIV and IDIV

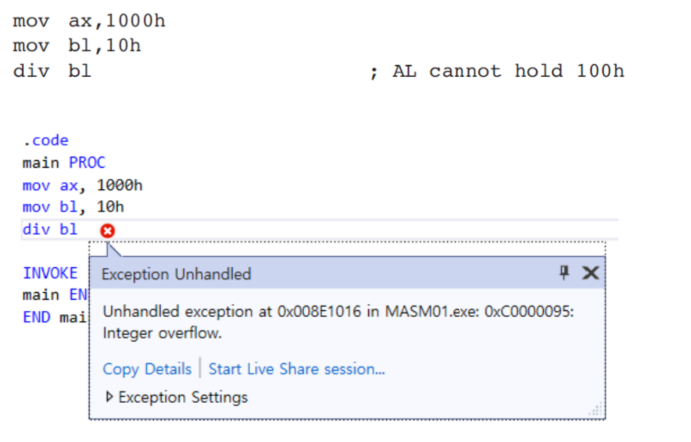
Divide Overflow
- If a division operand produces a quotient that will not fit into the destination operand, a divide overflow condition results
  - This causes a processor exception and halts the current program
  - E.g.) A divide overflow: the quotient (100h) is too large for the 8-bit AL destination register
If a division operand produces a quotient that will not fit into the destination operand, a divide overflow condition results
- This causes a processor exception and halts the current program
- E.g.) A divide overflow: the quotient (100h) is too large for the 8-bit AL destination register
A suggestion
- Use a 32-bit divisor and 64-bit dividend to reduce the probability of a divide overflow condition
- E.g.) The divisor is EBX, and the dividend is placed in the 64-bit combined EDX and EAX registers
```
mov eax, 1000h
cdq
mov ebx, 10h
div ebx				; EAX = 00000100h
```
To prevent division by zero, test the divisor before dividing

mov ax,dividend
mov bl,divisor
cmp bl,0			; check the divisor
je NoDivideZero		; zero? display error
div bl				; not zero: continue
.
.
NoDivideZero		; (display "Attempt to divide by zero")

6. Implementing Arithmetic Expressions

The benefits of implementing arithmetic expressions
- You can learn how compilers optimize code
- Also, you can implement better error checking than a typical compiler by checking the size of the product following multiplication operations
  - Most high-level language compilers ignore the upper 32 bits of the product when multiplying two 32-bit operands
  - In assembly language, however, you can use the Carry and Overflow flags to tell you when the product does not fit into 32 bits
Example 1
- A C++ statement using unsigned 32-bit integers: var4 = (var1 + var2) * var3;

	mov eax,var1
	add eax,var2
	mul var3			; EAX = EAX * var3
	jc tooBig			; unsigned overflow?
	mov var4,eax
	jmp next
tooBig:					; display error message

Example 2
- A C++ statement using unsigned 32-bit integers: var4 = (var1 * 5) / (var2 - 3);

mov eax, var1			; left side
mov ebx, 5
mul ebx					; EDX:EAX = product
mov ebx, var2			; right side
sub ebx,3
div ebx					; final division
mov var4,eax

Example 3
- A C++ statement using signed 32-bit integers: var4 = (var1 * -5) / (-var2 % var3);

mov eax,var2			; begin right side
neg eax
cdq						; sign-extend dividend
idiv var3				; EDX = remainder
mov ebx, edx			; EBC = right side
mov eax, -5				; begin left side
imul var1				; EDX:EAX = left side
idiv ebx				; final division
mov var4, eax			; quotient

Shy

스벨트 자바스크립트 익히는중...

이전 포스트