LeetCode - 118 Pascal's Triangle

개요

LeetCode 118번 문제 Pascal's Triangle 입니다.

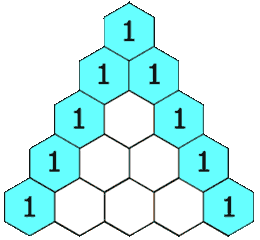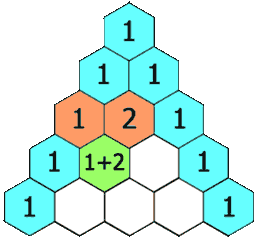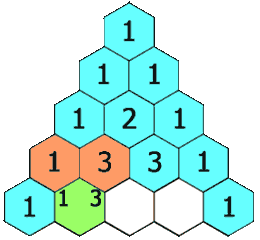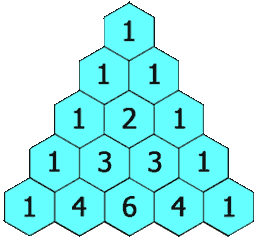
위에서 보이는 것 처럼, 삼각형 내부에 있는 수는 직접적으로 붙어 있는 위 열의 두 수를 더한 결과로 이루어져 있습니다.

조건

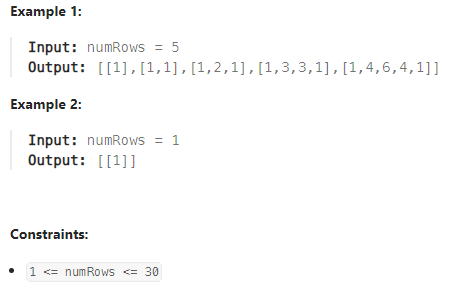
입력값: 정수형 단일 값 numRows (삼각형을 이루고 있는 열의 수)

출력값: 2차원 정수형 배열 (열이 numRows개인 Pascal's Triangle)

제한사항: 1 <= numRows <= 20

풀이

차근차근 접근해보도록 하겠습니다.

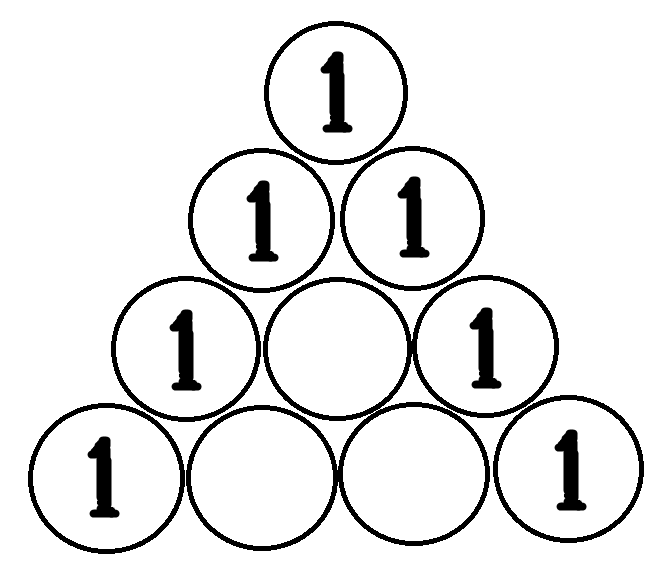
초기 Pascal's Triangle은 numRows=2입니다.

// Pascal's Triangle
dp = [
	[1],
	[1, 1],
	[1, null, 1],
	[1, null, null, 1],
]

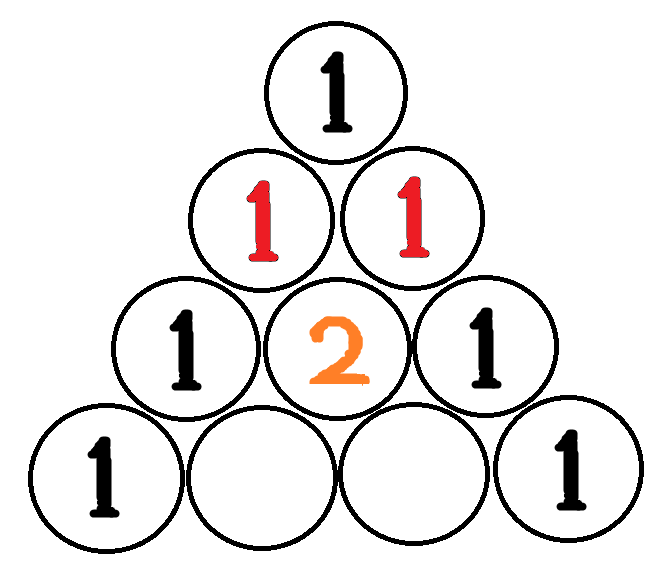
현재 위치에서 가장 인접해 있는, 위 열의 두 개의 값을 서로 더합니다.
계산 결과를 현재 위치에 저장합니다.
numRows=3일 때의 Pascal's Triangle이 만들어졌습니다.

// index_start -> 0
dp[2][1] = dp[1][0] + dp[1][1]

// Pascal's Triangle
dp = [
	[1],
	[1, 1],
	[1, 2, 1],
	[1, null, null, 1],
]

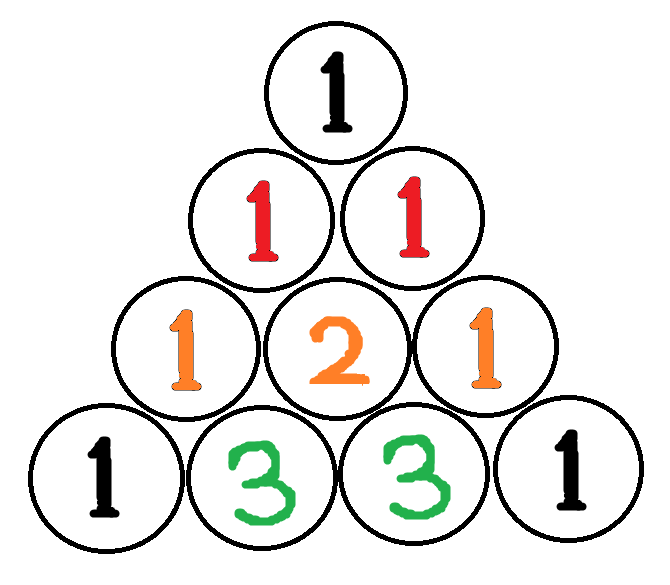
다음 열로 넘어가 위 과정을 반복합니다.
numRows=4일 때의 Pascal's Triangle이 만들어졌습니다.

// index_start -> 0
dp[3][1] = dp[2][0] + dp[2][1]
dp[3][2] = dp[2][1] + dp[2][2]

// Pascal's Triangle
dp = [
	[1],
	[1, 1],
	[1, 2, 1],
	[1, 3, 3, 1],
]

이 과정을 계속 반복하면 numRows=N일 때의 Pascal's Triangle을 만들 수 있습니다.

dp[2][1] = dp[1][0] + dp[1][1]

dp[3][1] = dp[2][0] + dp[2][1]
dp[3][2] = dp[2][1] + dp[2][2]

dp[4][1] = dp[3][0] + dp[3][1]
dp[4][2] = dp[3][1] + dp[3][2]
dp[4][3] = dp[3][2] + dp[3][3]

dp[5][1] = dp[4][0] + dp[4][1]
dp[5][2] = dp[4][1] + dp[4][2]
dp[5][3] = dp[4][2] + dp[4][3]
dp[5][4] = dp[4][3] + dp[4][4]
...

결국 핵심은, 위 열에서의 계산 결과가 아래 열에서 해답의 열쇠가 된다는 점입니다. 이 점을 이용하여 풀어봅시다.

pseudo code를 작성해보겠습니다.

<pseudo code>

// 1. Pascal's Triangle 구성
N = numRows			 // Rows & Columns by Pascal's Triangle
int[N] dp = [null, ] // Pascal's Triangle

for i in 0 to N:
	int[i] row = [1, ]
	dp[i] = row
    
// 2. Dynamic Programming을 이용해 해답 구하기
for i in 2 to N:
	for j in 1 to i:
    	dp[i][j] = dp[i-1][j-1] + dp[i-1][j]


return dp

첫 번째 for문에서 Pascal's Triangle을 제작하기 위해 초기 2차원 배열을 구성합니다. 해당 배열은 numRows개의 열을 가집니다. 두 번째 for문에서 Pascal's Triangle을 제작합니다.

최종 코드는 다음과 같습니다.

<Python>

class Solution:
    def generate(self, numRows: int) -> List[List[int]]:
    	# 1. Pascal's Triangle 구성
        dp = [[1] * i for i in range(1, numRows+1)]
		
        # 2. Dynamic Programming을 이용해 해답 구하기
        for i in range(2, numRows):
            for j in range(1, i):
                print(i, j)
                dp[i][j] = dp[i-1][j-1] + dp[i-1][j]

        return dp

자료 출처

Pascal's Triangle image - https://leetcode.com/problems/pascals-triangle/description/