1. Probability

1.1 Introduction

• 확률은 불확실성을 수량화하는 수학적 언어
• 확률론 기저의 기본 개념들을 소개
• 가능한 결과들의 집합인 sample space로 시작

1.2 Sample Spaces and Events

• Sample space $\Omega$는 실험에서 가능한 결과들의 집합
• Sample space 안의 포인트 $\omega$는 sample outcomes, realizations, elements로 불림
• Sample space의 부분집합들을 Events로 부른다.
• $A_i \cap A_j, i \not=j$ → disjoint or mutually exclusive
• Indicator function

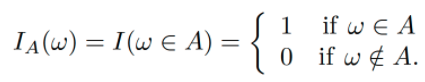
• monotone increasing, monotone decreasing 모두 $A_n\to A$로 표현

1.3 Probability

• $\mathbb P(A)$: Probability of A, Probability distribution of A, Probability measure of A
• The three axioms of $\mathbb P$

• P(A)에 대한 두 가지 보편적인 해석

  • The frequency interpretation

    반복 수행에서 A가 참인 시행 횟수의 비율

    ex) 동전의 앞면이 나올 확률이 1/2일 때 동전의 토스 횟수를 늘릴 때 앞면이 나오는 시행 횟수 비율이 1/2로 가는 경향을 보임

    무한의 시행 횟수의 동전을 토스한다고 할 때 나오는 비율을 이상적인 상수 값으로 제한함

  • The degree-of-belief interpretation

    관찰자가 A가 참이 될 것이라는 믿음의 강도를 측정한 것

• 두 가지 보편적인 해석 모두 세 가지 공리를 만족해야한다.
• Statistical inference를 다루기 전까지는 두 가지 해석 방법에는 차이가 없다.
• 세 가지 axiom으로부터 유도할 수 있는 식

1.6 Lemma

1.8 Theorem (Continuity of Probabilities)

$If A_n\to A, then \ \ \mathbb P(A_n)\to\mathbb P(A)\ \ as\ n\to \infin$

$A_n$을 monotone increasing이라고 가정

$A=\lim_{n \to \infin}A_n=\cup^\infin_{i=1}A_i$

$B_1=A_1, B_2= \{\omega\in\Omega:\omega\in A_2,\omega \not \in A_1 \}$

$B_3= \{\omega\in\Omega:\omega\in A_3,\omega \not \in A_2,\omega \not \in A_1 \} ...$

• $B_1,B_2,...$는 서로 겹치는 요소들이 없기 때문에 disjoint하다.
• $A_n=\cup^n_{i=1}A_i=\cup^n_{i=1}B_i$, for each $n$
• $\cup^\infin_{i=1}A_i=\cup^\infin_{i=1}B_i$
• Axiom 3에 의해 (서로 disjoint한 event들의 합집합의 확률은 event들의 확률의 합과 같다)

1.4 Probability on Finite Sample Spaces

• Sample space $\Omega$가 유한한 개수의 요소를 가지는 경우를 가정
• $|A|:A$가 갖고 있는 요소들의 개수
• $\Omega$가 유한한 개수를 가지고 각 결과들이 나올 가능성이 같다면
• $\mathbb P(A)=\cfrac{|A|}{|\Omega|}$ → Uniform probability distribution
  
• 확률을 계산하기 위해서 event $A$안의 포인트들의 개수를 세어야한다.
• Point들의 개수를 세는 것을 combinatorial methods라고 부름
• $n$개의 요소가 주어졌을 때

  • 순서를 나열하는 방법의 개수

    

  • $0!=1$로 정의

  • n개의 요소로부터 k개의 요소를 구별된 방법으로 고르는 방법의 수

    

    

1.5 Independent Events

• 동전을 두 번 던질 때 앞면이 두번 나오는 확률을 $\frac{1}{2}\times \frac{1}{2}$로 계산함 → 두 번의 토스가 독립적인 사건으로 여기기 때문에 확률을 곱함
  
• 독립의 공식적인 정의

• 독립은 두 가지 별개의 방법으로 발생한다.
  • 두 이벤트가 독립이라고 가정함 ex) 동전의 토스의 경우 두 번째 토스에서 첫 번째 토스의 정보를 저장할 메모리가 없음
    
  • $P(AB)=P(A)P(B)$를 증명해서 독립임을 보임
• 두 가지 disjoint event A,B는 P(AB)가 0이 되기 때문에 독립이 아님

1.6 Conditional Probability

• P(A|B)는 B가 발생하는 횟수 중 A가 발생하는 횟수
• 고정된 B에 대해서 P(B)>0, P(.|B)는 확률이기에 세 개의 공리를 만족
• P(A|B) ≥0, $P(\Omega|B)=1$
• $A_1,A_2,...$가 서로 disjoint할 때

• Bar 왼쪽에 대해서만 공리 3이 성립

• 조건부 확률의 먼저 주어지는 이벤트가 바뀌면 일반적으로 값이 같지는 않다.

$P(A|B) \not=P(B|A)$

ex) 홍역이 있을 경우 반점이 생길 확률은 1이지만 반점이 생겼을 때 홍역일 확률은 1이 아님

1.14 Lemma

• A와 B가 독립인 이벤트 일 때 P(A|B)=P(A)
• P(AB)=P(A|B)P(B)=P(B|A)P(A)
• P(AB)=P(A)P(B)=P(A|B)P(B) ⇒ P(A|B)=P(A)
• A와 B가 독립일 때는 이벤트 B는 A의 확률에 영향을 주지 않는다

1.7 Bayes’ Theorem

• Expert system과 Bayes’ nets의 기초

1.16 Theorem (The Law of Total Probability)

• $A_1,...,A_k$로 sample space가 이루어질 때 임의의 이벤트 B에 대해

• 증명

$C_j=BA_j, C_1,...,C_k$가 disjoint라고 가정

1.18 Remark

• $P(A_i)$: Prior of probability of A
• $P(A_i|B)$: Posterior probability of A

1.19 Example

$P(A_1|B)=\cfrac{P(A_1B)}{P(B)}=\cfrac{P(B|A_1)P(A_1)}{\sum_j P(B|A_j)P(A_j)}=\cfrac{P(B|A_1)P(A_1)}{P(B|A_1)P(A_1)+P(B|A_2)P(A_2)+P(B|A_3)P(A_3)}=\cfrac{0.9\times0.7}{0.9\times0.7+0.2\times0.01+0.01\times0.1}=0.995$